Введение в равномерное распределение

Равномерное распределение — это распределение вероятностей, в котором каждое значение между интервалом от a до b имеет одинаковую вероятность появления.

Если случайная величина X имеет равномерное распределение, то вероятность того, что X примет значение между x ₁ и x ₂ , можно найти по следующей формуле:

P(x ₁ < X < x ₂ ) = (x ₂ – x ₁ ) / (b – а)

Золото:

• x ₁ : меньшая процентная ставка
• x ₂ : верхнее интересующее значение
• а: минимально возможное значение
• б: максимально возможное значение

Например, предположим, что вес дельфинов равномерно распределен между 100 и 150 фунтами.

Если мы выберем дельфина наугад, мы можем использовать приведенную выше формулу, чтобы определить вероятность того, что выбранный дельфин весит от 120 до 130 фунтов:

• P(120 < X < 130) = (130 – 120) / (150 – 100)
• Р(120 <Х<130) = 10/50
• Р(120 <Х <130) = 0,2

Вероятность того, что выбранный дельфин весит от 120 до 130 фунтов, равна 0,2 .

Визуализация равномерного распределения

Если мы создадим график плотности для визуализации равномерного распределения, он будет выглядеть следующим образом:

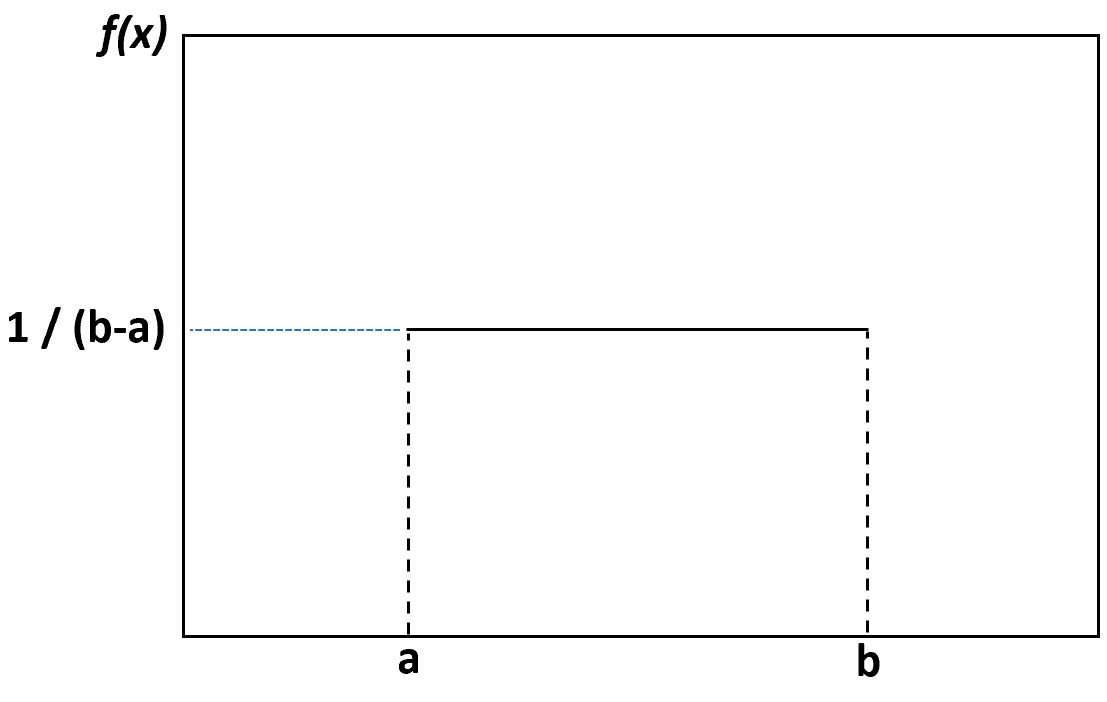
Каждое значение между нижним пределом a и верхним пределом b имеет одинаковую вероятность появления, а любое значение за пределами этих пределов имеет вероятность, равную нулю.

Например, в нашем предыдущем примере мы сказали, что вес дельфинов равномерно распределен между 100 и 150 фунтами. Вот как можно визуализировать это распределение:

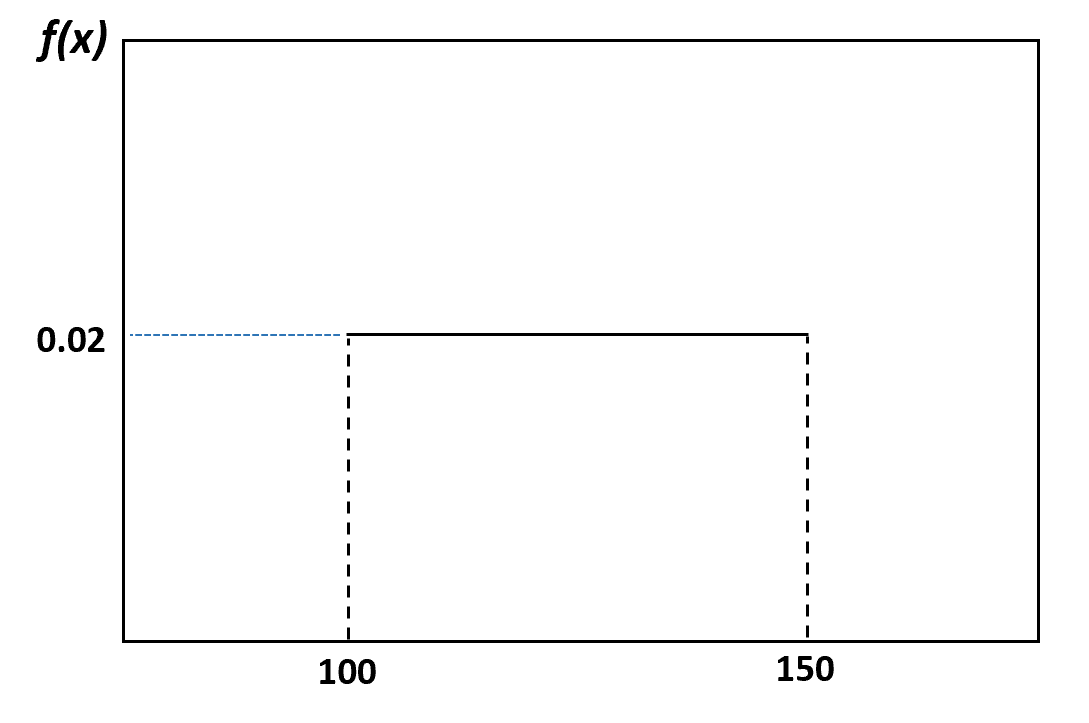
А вероятность того, что случайно выбранный дельфин весит от 120 до 130 фунтов, можно визуализировать следующим образом:

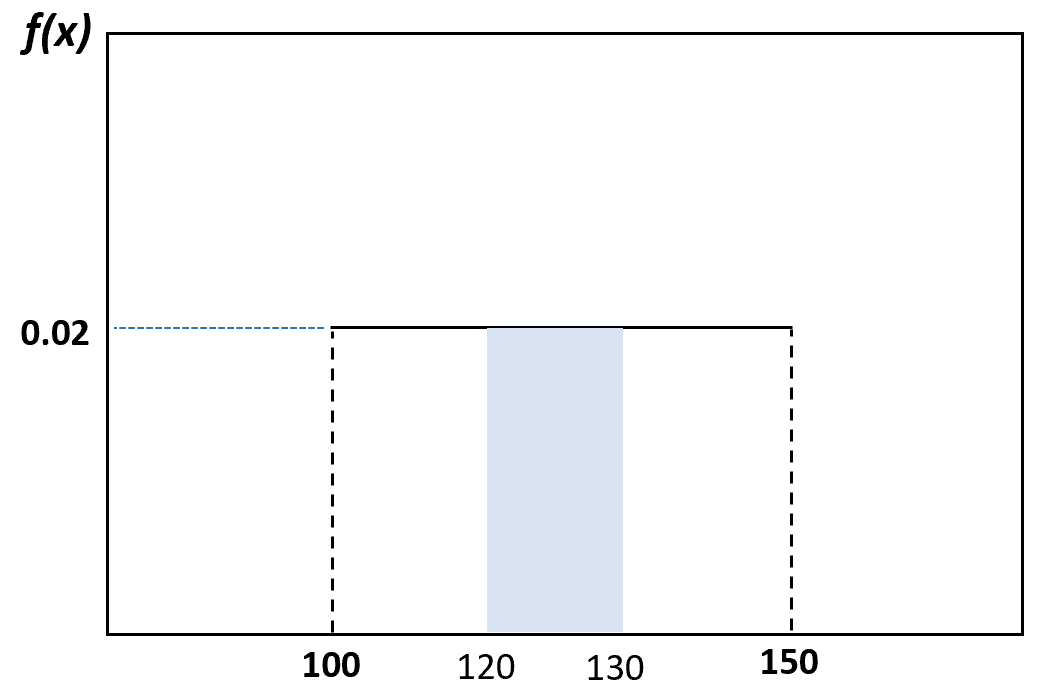
Свойства равномерного распределения

Равномерное распределение обладает следующими свойствами:

• Среднее: (а + б)/2
• Медиана: (a + b) / 2
• Стандартное отклонение: √ (б – а) ^2/12
• Разница: (б – а) ^2/12

Например, предположим, что вес дельфинов равномерно распределен между 100 и 150 фунтами.

Мы могли бы вычислить следующие свойства для этого распределения:

• Средний вес: (a + b)/2 = (150 + 100)/2 = 125
• Средний вес: (a + b) / 2 = (150 + 100) / 2 = 125
• Стандартное отклонение веса: √ (150 – 100) ^2/12 = 14,43.
• Изменение веса: (150 – 100) ^2/12 = 208,33

Проблемы с единой практикой распределения

Используйте следующие практические задачи, чтобы проверить свои знания о равномерном распределении.

Вопрос 1: Автобус приходит на остановку каждые 20 минут. Если вы приедете на автобусную остановку, какова вероятность того, что автобус прибудет через 8 минут или меньше?

Решение 1. Минимальное время ожидания — 0 минут, максимальное — 20 минут. Нижнее значение процентной ставки составляет 0 минут, а верхнее значение процентной ставки составляет 8 минут.

Итак, мы рассчитаем вероятность следующим образом:

Р(0 <Х<8) = (8-0)/(20-0) = 8/20 = 0,4 .

Вопрос 2: Продолжительность игры НБА равномерно распределяется между 120 и 170 минутами. Какова вероятность того, что случайно выбранная игра НБА продлится более 155 минут?

Решение 2. Минимальная продолжительность — 120 минут, максимальная — 170 минут. Нижнее процентное значение составляет 155 минут, а верхнее процентное значение — 170 минут.

Итак, мы рассчитаем вероятность следующим образом:

Р(155 <Х<170) = (170-155)/(170-120) = 15/50 = 0,3 .

Вопрос 3: Вес определенного вида лягушек равномерно распределен между 15 и 25 граммами. Если вы наугад выберете лягушку, какова вероятность того, что она будет весить от 17 до 19 граммов?

Решение 3. Минимальный вес — 15 грамм, максимальный — 25 грамм. Нижняя процентная ставка составляет 17 граммов, а верхняя процентная ставка составляет 19 граммов.

Итак, мы рассчитаем вероятность следующим образом:

Р(17 <Х<19) = (19-17)/(25-15) = 2/10 = 0,2 .

Примечание. Мы можем использовать калькулятор равномерного распределения, чтобы проверить ответы на каждую из этих задач.