Размер эффекта: что это такое и почему это важно
«Статистическая значимость — наименее интересная вещь в результатах. Вам необходимо описывать результаты с точки зрения масштабов: не только лечение влияет на людей, но и то, насколько оно влияет на них. -Джин В. Гласс
В статистике мы часто используем значения p , чтобы определить, существует ли статистически значимая разница между двумя группами.
Например, предположим, что мы хотим знать, приводят ли два разных метода обучения к разным результатам тестов. Итак, у нас есть группа из 20 студентов, которые используют один метод обучения для подготовки к тесту, в то время как другая группа из 20 студентов использует другой метод обучения. Затем мы даем каждому студенту одинаковый тест.
После запуска t-теста с двумя выборками для определения разницы средних значений мы обнаруживаем, что значение p для теста составляет 0,001. Если мы используем уровень значимости 0,05, это означает, что существует статистически значимая разница между средними результатами двух групп. Итак, методика исследования оказывает влияние на результаты тестирования.
Однако, хотя значение p говорит нам о том, что техника обучения влияет на результаты тестов, оно не говорит нам о величине этого влияния. Чтобы это понять, нам нужно знать размер эффекта .
Что такое размер эффекта?
Размер эффекта — это способ количественной оценки разницы между двумя группами.
Хотя значение p может сказать нам, существует ли статистически значимая разница между двумя группами, размер эффекта может сказать нам , насколько велика эта разница на самом деле. На практике размеры эффекта гораздо интереснее и полезнее знать, чем значения p.
Существует три способа измерения размера эффекта, в зависимости от типа анализа, который вы проводите:
1. Стандартизированная средняя разница
Если вы хотите изучить среднюю разницу между двумя группами, подходящим способом расчета размера эффекта является использование стандартизированной средней разницы . Самая популярная формула известна как d Коэна, которая рассчитывается следующим образом:
D Коэна = ( x1 – x2 )/ s
где x 1 и x 2 — выборочные средние значения группы 1 и группы 2 соответственно, а s — стандартное отклонение генеральной совокупности, из которой были выбраны две группы.
Используя эту формулу, размер эффекта легко интерпретировать:
- Значение A d, равное 1, указывает на то, что средние значения двух групп различаются на одно стандартное отклонение.
- Значение A d , равное 2, означает, что средние значения группы отличаются на два стандартных отклонения.
- Ad , равный 2,5, означает, что два средних значения различаются на 2,5 стандартных отклонения и так далее.
Другой способ интерпретации размера эффекта: размер эффекта 0,3 означает, что балл среднего человека в группе 2 на 0,3 стандартного отклонения выше среднего показателя человека в группе 1 и, следовательно, превышает на 62% баллы в группе 1 . .
В следующей таблице показаны различные размеры эффекта и соответствующие им процентили:
| Размер эффекта | Процент группы 2 , который был бы ниже среднего показателя людей в группе 1 |
|---|---|
| 0,0 | 50% |
| 0,2 | 58% |
| 0,4 | 66% |
| 0,6 | 73% |
| 0,8 | 79% |
| 1.0 | 84% |
| 1.2 | 88% |
| 1,4 | 92% |
| 1,6 | 95% |
| 1,8 | 96% |
| 2.0 | 98% |
| 2,5 | 99% |
| 3.0 | 99,9% |
Чем больше размер эффекта, тем больше разница между средним человеком в каждой группе.
В общем, значение a d 0,2 или меньше считается небольшим размером эффекта, значение a d около 0,5 считается средним размером эффекта, а значение a d 0,8 или больше считается большим размером эффекта.
Таким образом, если средние значения двух групп не отличаются хотя бы на 0,2 стандартных отклонения, разница незначительна, даже если значение p статистически значимо.
2. Коэффициент корреляции
Если вы хотите изучить количественную связь между двумя переменными, наиболее распространенным способом расчета размера эффекта является использование коэффициента корреляции Пирсона . Это мера линейной связи между двумя переменными X и Y. Она имеет значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными.
- 0 указывает на отсутствие линейной корреляции между двумя переменными.
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Формула расчета коэффициента корреляции Пирсона довольно сложная, но для интересующихся ее можно найти здесь .
Чем дальше коэффициент корреляции от нуля, тем сильнее линейная связь между двумя переменными. В этом также можно убедиться, создав простую диаграмму рассеяния значений переменных X и Y.
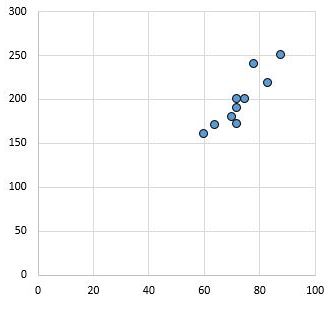
Например, следующая диаграмма рассеяния показывает значения двух переменных с коэффициентом корреляции r = 0,94.
Это значение далеко от нуля, что указывает на наличие сильной положительной связи между двумя переменными.
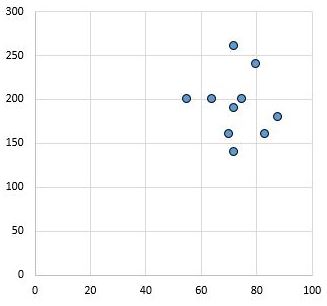
И наоборот, следующая диаграмма рассеяния показывает значения двух переменных, которые имеют коэффициент корреляции r = 0,03. Это значение близко к нулю, что указывает на то, что между двумя переменными практически нет связи.
В общем, величина эффекта считается небольшой, если значение коэффициента корреляции Пирсона r составляет около 0,1, средней, если r составляет около 0,3, и большой, если r равно или превышает 0,5.
3. Коэффициент шансов
Если вы хотите изучить шансы на успех в группе лечения по сравнению с шансами на успех в контрольной группе, наиболее распространенным способом расчета размера эффекта является использование отношения шансов .
Например, предположим, что у нас есть следующая таблица:
| Размер эффекта | #Успех | #Шахматы |
|---|---|---|
| Группа лечения | ИМЕЕТ | Б |
| Контрольная группа | ПРОТИВ | Д |
Отношение шансов будет рассчитываться следующим образом:
Коэффициент шансов = (AD) / (BC)
Чем дальше отношение шансов от 1, тем выше вероятность того, что лечение даст реальный эффект.
Преимущества использования размеров эффекта по сравнению с P-значениями
Размеры эффекта имеют несколько преимуществ перед значениями p:
1. Размер эффекта помогает нам лучше понять, насколько велика разница между двумя группами или насколько сильна связь между двумя группами. Значение p может только сказать нам, существует ли значительная разница или значимая связь.
2. В отличие от значений p, размеры эффекта можно использовать для количественного сравнения результатов различных исследований, проведенных в разных условиях. По этой причине в метаанализе часто используются размеры эффекта.
3. На значения P могут влиять большие размеры выборки. Чем больше размер выборки, тем выше статистическая мощность проверки гипотезы, что позволяет обнаружить даже небольшие эффекты. Это может привести к низким значениям p, несмотря на небольшие размеры эффекта, которые могут не иметь практического значения.
Простой пример может наглядно это проиллюстрировать: предположим, мы хотим знать, приводят ли два метода обучения к разным результатам тестов. У нас есть группа из 20 студентов, использующих одну технику обучения, а другая группа из 20 студентов, использующих другую технику обучения. Затем мы даем каждому студенту одинаковый тест.
Средний балл группы 1 — 90,65 , средний балл группы 2 — 90,75 . Стандартное отклонение для образца 1 составляет 2,77 , а стандартное отклонение для образца 2 — 2,78 .
Когда мы выполняем независимый двухвыборочный t-тест, оказывается, что статистика теста равна -0,113 , а соответствующее значение p равно 0,91 . Разница между средними баллами тестов не является статистически значимой.
Однако представьте, что размеры выборок обеих выборок составляли 200 , но средние значения и стандартные отклонения остались точно такими же.
В этом случае независимый двухвыборочный t-критерий покажет, что статистика теста равна -1,97 , а соответствующее значение p чуть ниже 0,05 . Разница между средними баллами тестов статистически значима.
Основная причина, по которой большие размеры выборки могут привести к статистически значимым выводам, связана с формулой, используемой для расчета статистики t- теста:
статистика теста t = [ ( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
Обратите внимание, что когда n 1 и n 2 малы, целочисленный знаменатель статистики t -теста мал. А если разделить на маленькое число, то получится большое число. Это означает, что статистика t- критерия будет большой, а соответствующее значение p будет небольшим, что приведет к статистически значимым результатам.
Какой размер эффекта считается хорошим?
Студенты часто задают вопрос: какой размер эффекта считается хорошим?
Короткий ответ: размер эффекта не может быть «хорошим» или «плохим», поскольку он просто измеряет размер разницы между двумя группами или силу связи между двумя группами.
Однако мы можем использовать следующие эмпирические правила, чтобы количественно определить, является ли величина эффекта маленькой, средней или большой:
Коэн Д:
- Значение A d 0,2 или менее считается малым размером эффекта.
- Значение A d 0,5 считается средней величиной эффекта.
- Значение A d 0,8 или выше считается большим размером эффекта.
Коэффициент корреляции Пирсона
- Абсолютное значение r около 0,1 считается небольшой величиной эффекта.
- Абсолютное значение r около 0,3 считается средней величиной эффекта.
- Абсолютное значение r больше 0,5 считается большой величиной эффекта.
Однако определение «сильной» корреляции может варьироваться от одной области к другой. Обратитесь к этой статье , чтобы лучше понять, что считается сильной корреляцией в различных отраслях.