Как выполнить знаковый ранговый тест уилкоксона
Знаковый ранговый критерий Уилкоксона — это непараметрическая версия парного t-критерия . Он используется для проверки того, существует ли значительная разница между двумя средними значениями генеральной совокупности.
Когда использовать знаковый ранговый критерий Уилкоксона
Используйте критерий знакового ранга Уилкоксона, если вы хотите использовать парный t-критерий, но распределение различий между парами сильно отличается от нормального .
Самый простой способ определить, не распределены ли различия нормально, — это создать гистограмму различий и посмотреть, следуют ли они нормальному, «колокольчатому» распределению.
Имейте в виду, что парный t-критерий достаточно устойчив к отклонениям от нормальности, поэтому отклонение от нормального распределения должно быть достаточно большим, чтобы оправдать использование критерия знакового ранга Уилкоксона.
Как пройти знаковый ранговый тест Уилкоксона
В следующем примере показано, как выполнить тест знакового ранга Уилкоксона.
Баскетбольный тренер хочет знать, увеличивает ли определенная программа тренировок количество штрафных бросков, выполняемых его игроками. Чтобы проверить это, он попросил 15 игроков выполнить по 20 штрафных бросков до и после тренировочной программы.
Поскольку каждый игрок может быть «в паре» сам с собой, тренер планировал использовать парный t-тест, чтобы определить, существует ли значительная разница между средним количеством штрафных бросков, выполненных до и после тренировочной программы. обучение.
Однако распределение различий оказывается ненормальным, поэтому вместо этого тренер использует знаковый ранговый критерий Уилкоксона.
В следующей таблице показано количество штрафных бросков, выполненных (из 20 попыток) каждым из 15 игроков до и после тренировочной программы:
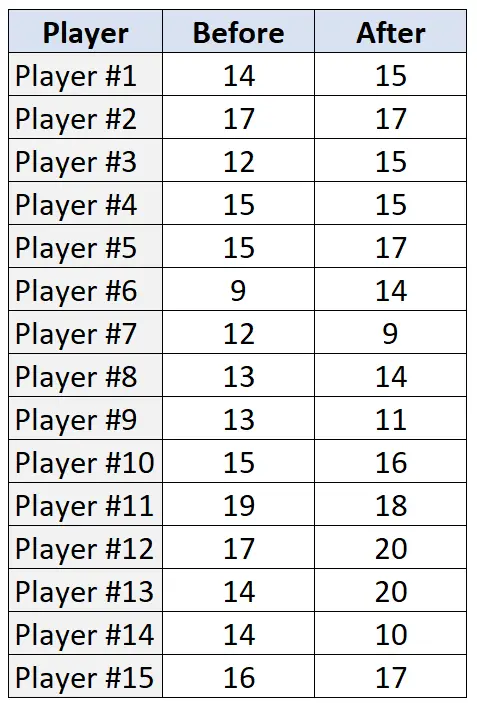
Шаг 1: Сформулируйте нулевую и альтернативную гипотезы.
H 0 : Медианная разница между двумя группами равна нулю.
Х А : Медианная разница отрицательна. (например, игроки делают меньше штрафных бросков перед участием в тренировочной программе)
Шаг 2: Найдите разницу и абсолютную разницу для каждой пары.
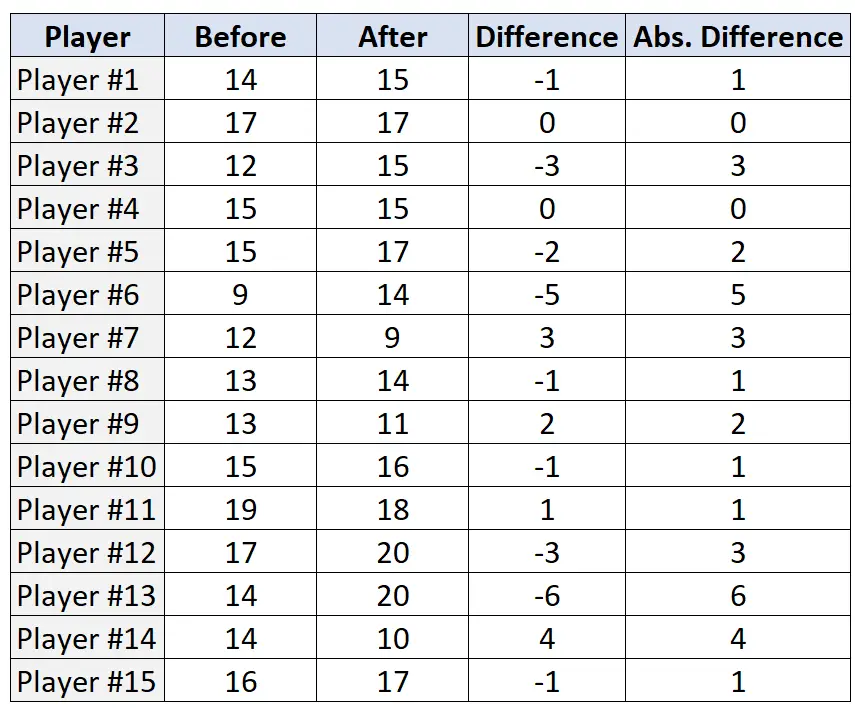
Шаг 3. Проранжируйте пары на основе абсолютных различий и присвойте ранг от наименьшего до наибольшего абсолютного различия. Игнорируйте пары, абсолютная разница которых равна «0», и назначайте средние ранги в случае ничьей.
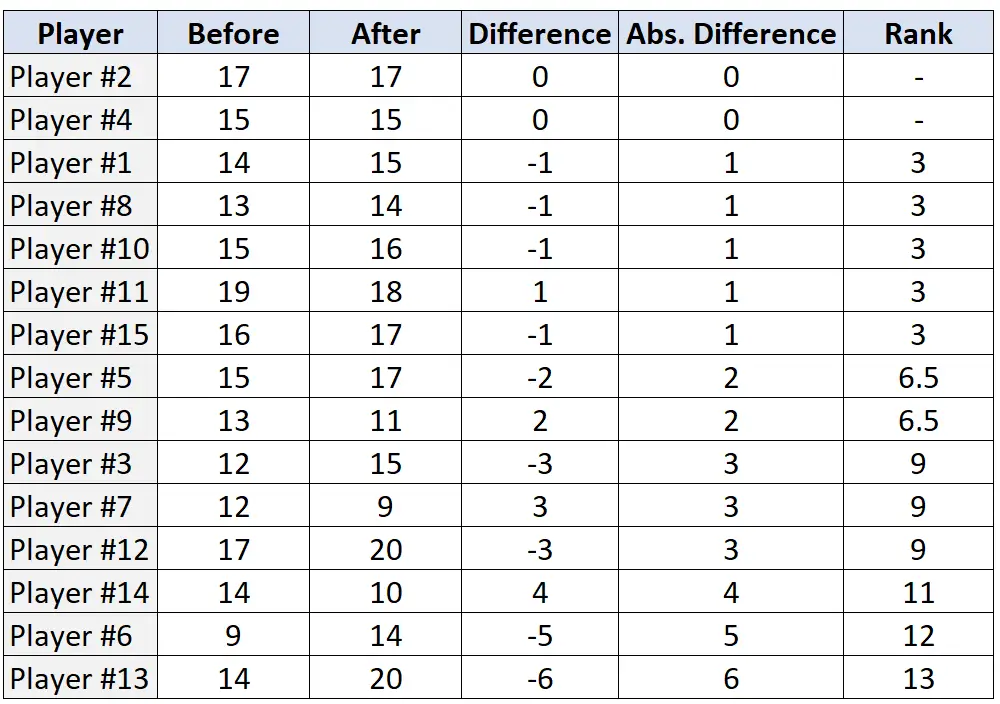
Шаг 4: Найдите сумму положительных и отрицательных рангов.
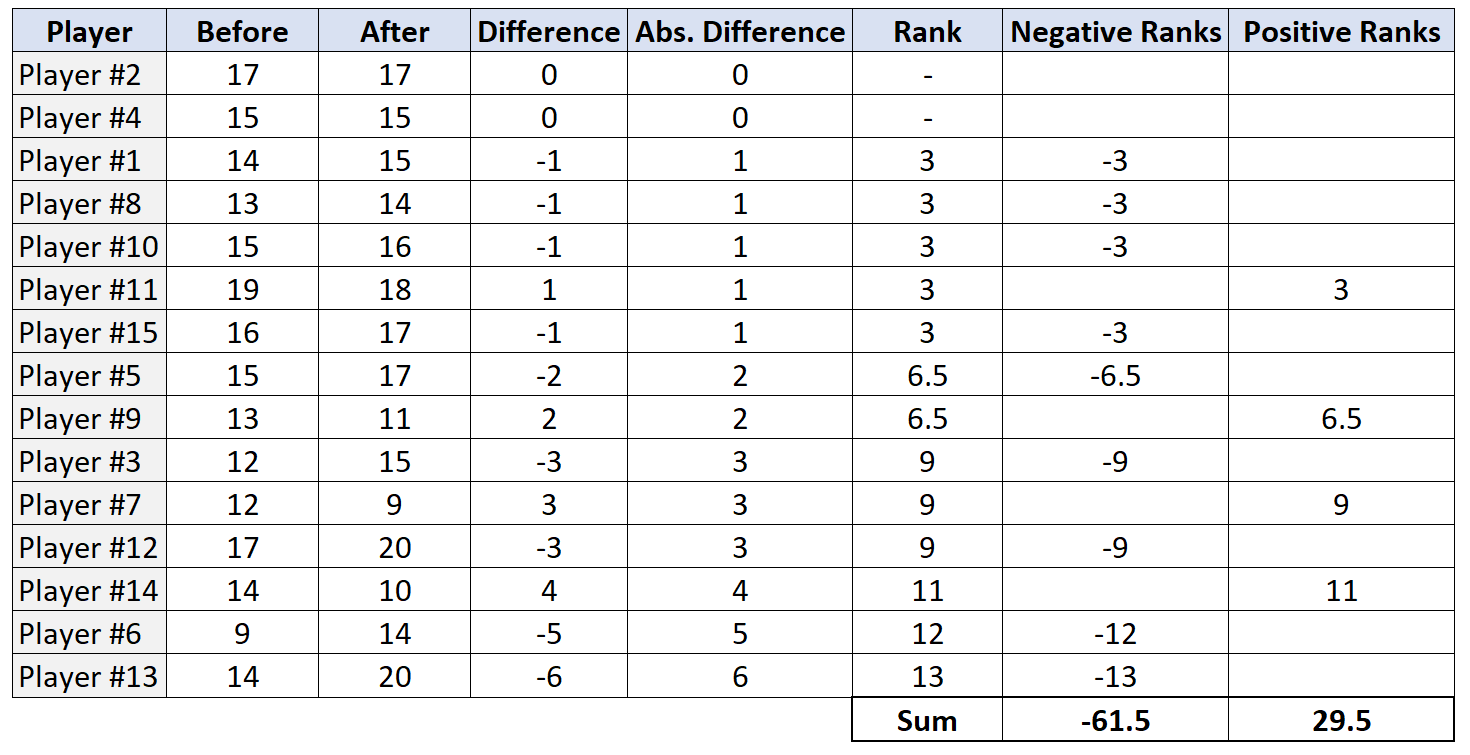
Шаг 5: Отклонить или не отвергать нулевую гипотезу.
Тестовая статистика W представляет собой наименьшее из абсолютных значений положительных и отрицательных рангов. В данном случае наименьшее значение равно 29,5. Итак, наша тестовая статистика равна W = 29,5 .
Чтобы определить, следует ли нам отвергнуть нулевую гипотезу, мы можем обратиться к критическому значению, найденному в таблице критических значений знакового рангового критерия Уилкоксона, которое соответствует n и выбранному альфа-уровню.
Если наша тестовая статистика W меньше или равна критическому значению в таблице, мы можем отвергнуть нулевую гипотезу. В противном случае мы не сможем отвергнуть нулевую гипотезу.
Критическое значение, которое соответствует уровню альфа 0,05 и n = 13 (общее количество пар минус две, для которых мы не вычислили ранг, поскольку у них наблюдалась разница 0), составляет 17 .
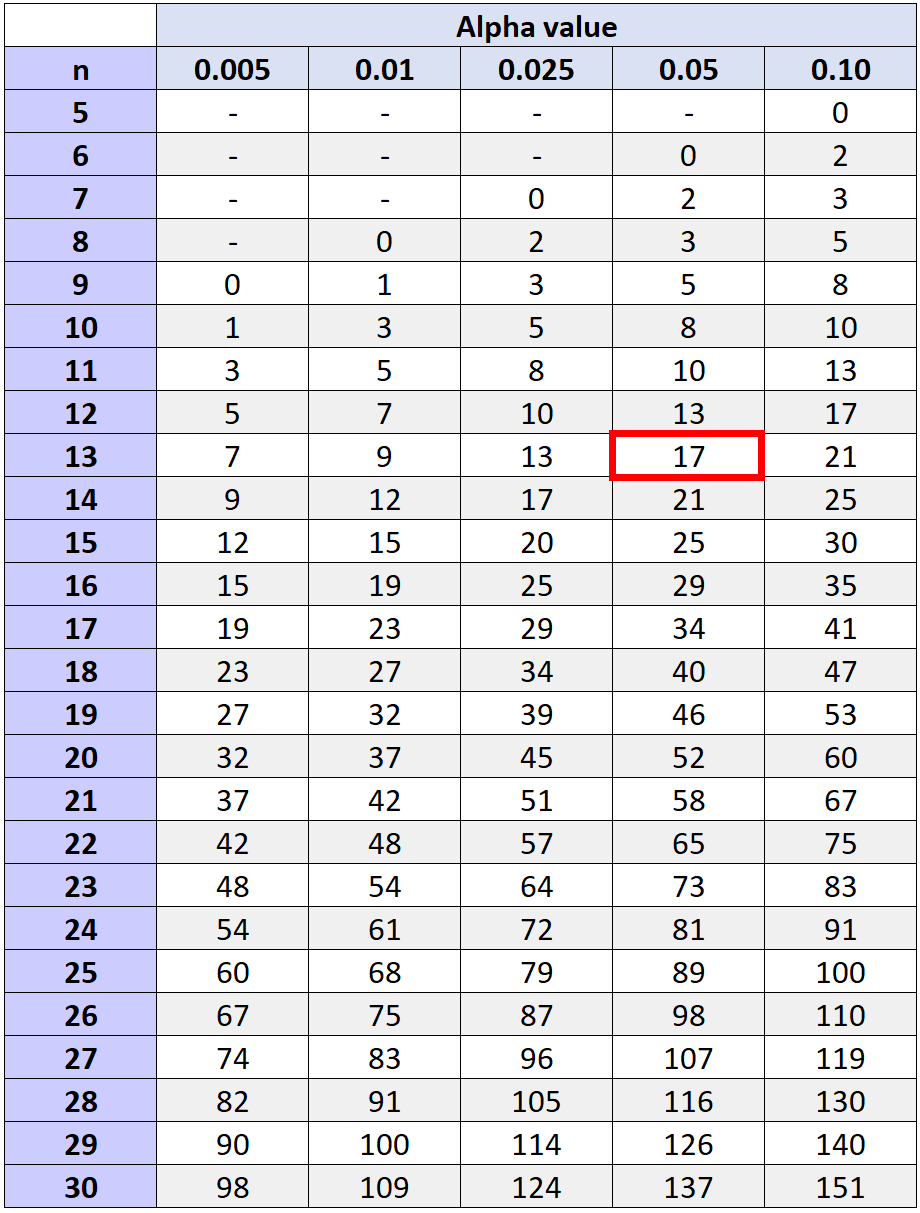
Поскольку наша тестовая статистика (W = 29,5) не меньше или равна 17, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных оснований утверждать, что программа тренировок приводит к значительному увеличению количества штрафных бросков, выполняемых игроками.
Примечание. Используйте калькулятор знаковых ранговых тестов Уилкоксона, если вы хотите выполнить тест с помощью калькулятора, а не вручную.