Как рассчитать выборочные распределения в excel

Выборочное распределение — это распределение вероятностей определенной статистики , основанное на множестве случайных выборок из одной совокупности .

В этом руководстве объясняется, как выполнить следующие действия с выборочными распределениями в Excel:

• Создайте выборочное распределение.
• Визуализируйте распределение выборки.
• Рассчитайте среднее и стандартное отклонение выборочного распределения.
• Рассчитайте вероятности распределения выборки.

Создание выборочного распределения в Excel

Предположим, мы хотим создать выборочное распределение, состоящее из 1000 выборок, в котором каждый размер выборки равен 20 и получается из нормального распределения со средним значением 5,3 и стандартным отклонением 9 .

Мы можем легко сделать это, введя следующую формулу в ячейку A2 нашей электронной таблицы:

 = NORM . INV ( RAND (), 5.3, 9)

Затем мы можем навести указатель мыши на правый нижний угол ячейки, пока не появится маленький + , и перетащить формулу на 20 ячеек вправо и на 1000 ячеек вниз:

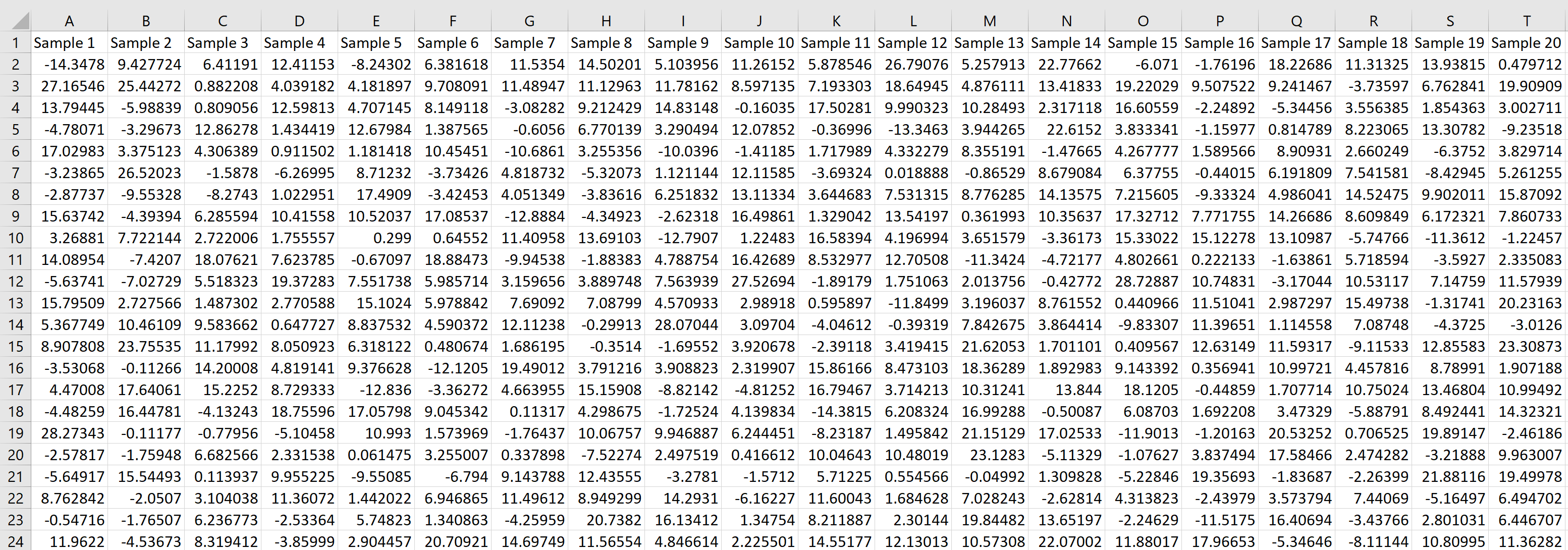
Каждая строка представляет собой выборку размером 20 человек, в которой каждое значение соответствует нормальному распределению со средним значением 5,3 и стандартным отклонением 9.

Найдите среднее и стандартное отклонение

Чтобы найти среднее и стандартное отклонение этого выборочного распределения выборочных средних, мы можем сначала найти среднее значение каждой выборки, введя следующую формулу в ячейку U2 нашего рабочего листа:

 = AVERAGE (A2:T2)

Затем мы можем навести указатель мыши на правый нижний угол ячейки, пока не появится маленький + , и дважды щелкнуть, чтобы скопировать эту формулу во все остальные ячейки в столбце U:

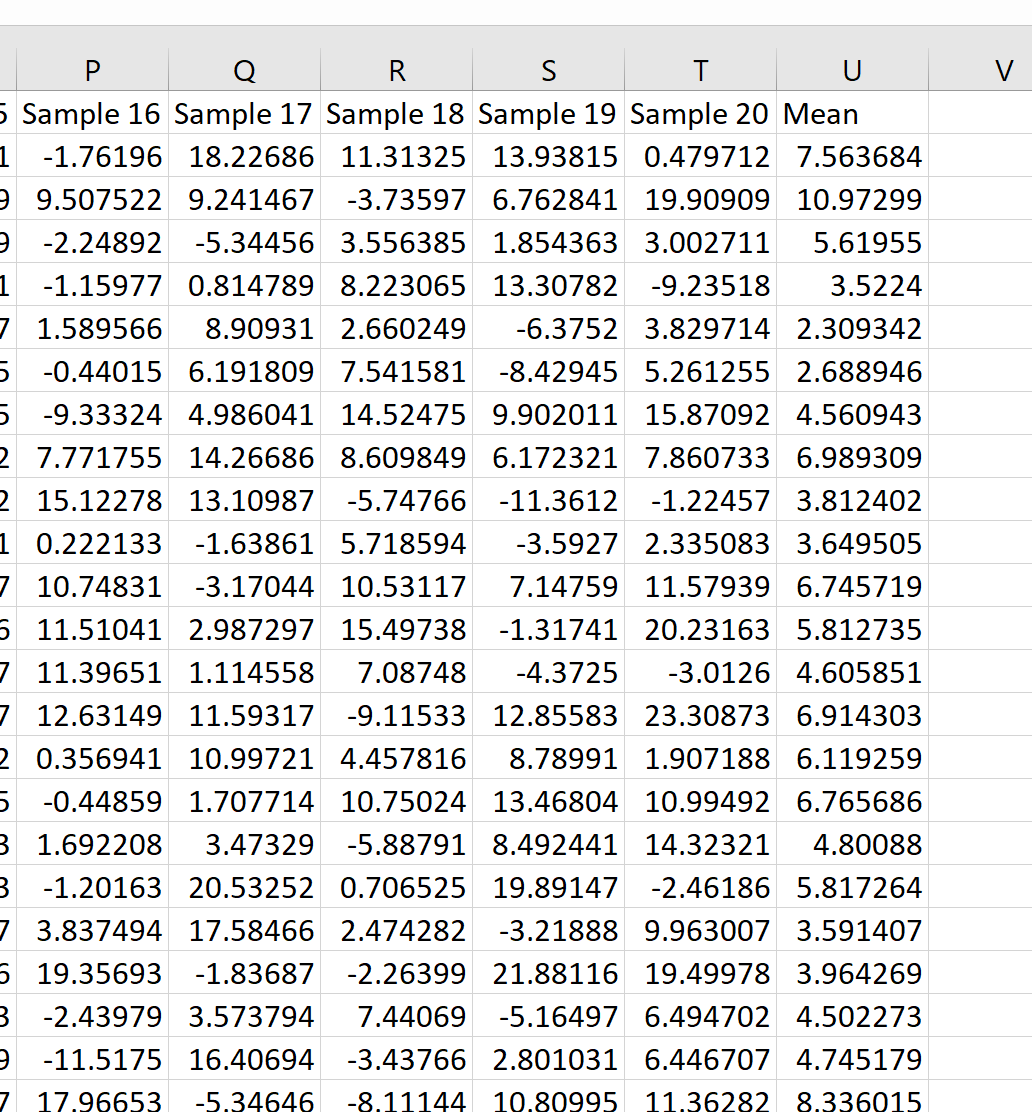
Мы видим, что в первом образце среднее значение было 7,563684, во втором — 10,97299 и так далее.

Затем мы можем использовать следующие формулы для расчета среднего и стандартного отклонения выборочных средних:

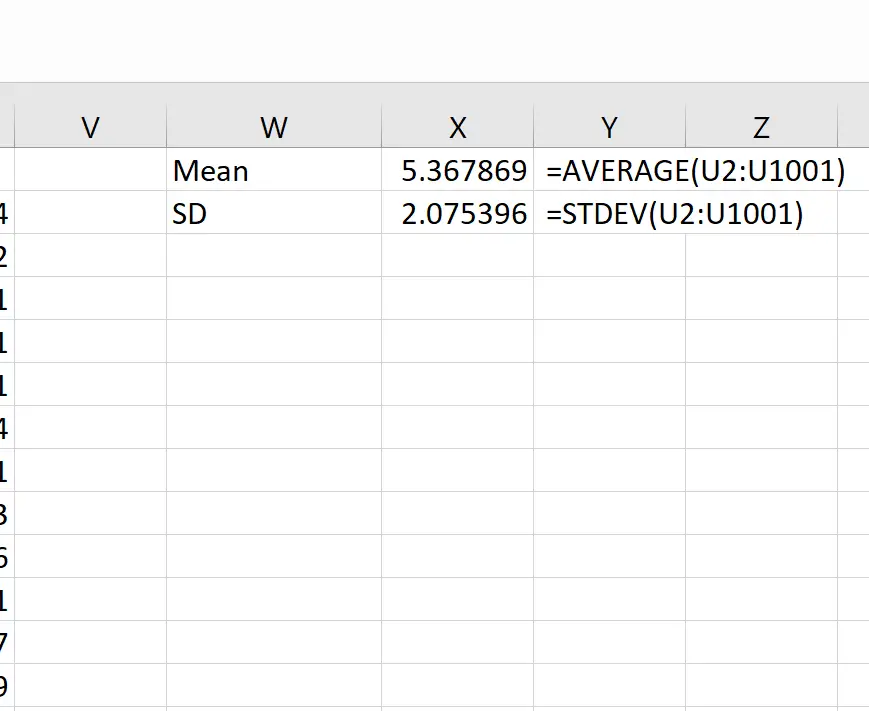
Теоретически среднее значение выборочного распределения должно составлять 5,3. Мы видим, что фактическое среднее значение выборки в этом примере равно 5,367869 , что близко к 5,3.

И теоретически стандартное отклонение выборочного распределения должно быть равно s/√n, что составит 9/√20 = 2,012. Мы видим, что фактическое стандартное отклонение выборочного распределения составляет 2,075396 , что близко к 2,012.

Визуализация распределения выборки

Мы также можем создать простую гистограмму, чтобы визуализировать выборочное распределение средних значений выборки.

Для этого просто выделите все средние значения выборки в столбце U, перейдите на вкладку «Вставка» , а затем выберите параметр «Гистограмма» в разделе «Диаграммы» .

Это дает следующую гистограмму:

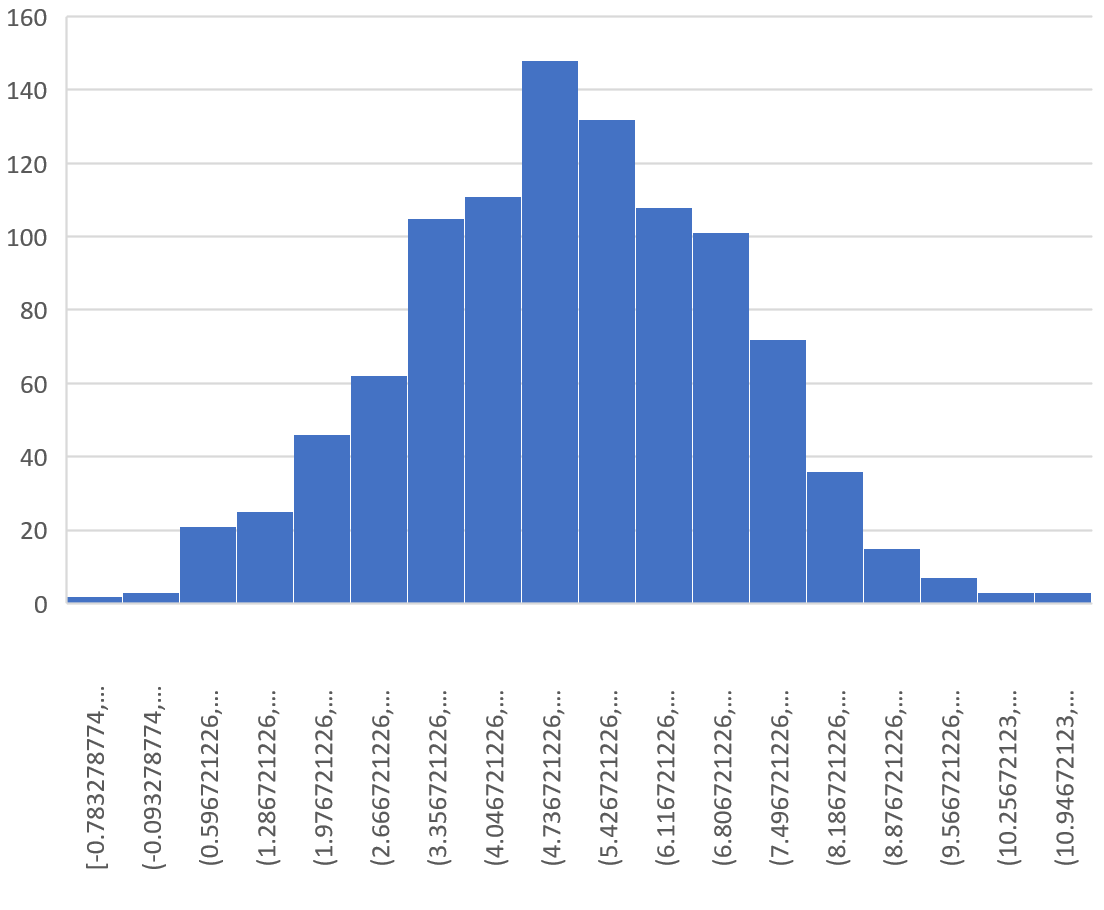
Видно, что распределение выборки имеет колоколообразную форму с пиком около значения 5.

Однако из хвостов распределения мы видим, что некоторые выборки имели средние значения больше 10, а другие — меньше 0.

Вычислить вероятности

Мы также можем рассчитать вероятность получения определенного значения выборочного среднего на основе среднего значения генеральной совокупности, стандартного отклонения генеральной совокупности и размера выборки.

Например, мы можем использовать следующую формулу, чтобы найти вероятность того, что среднее значение выборки меньше или равно 6, учитывая, что среднее значение генеральной совокупности равно 5,3, стандартное отклонение генеральной совокупности равно 9, а размер выборки равен:

 = COUNTIF (U2:U1001, " <=6 ")/ COUNT (U2:U1001)

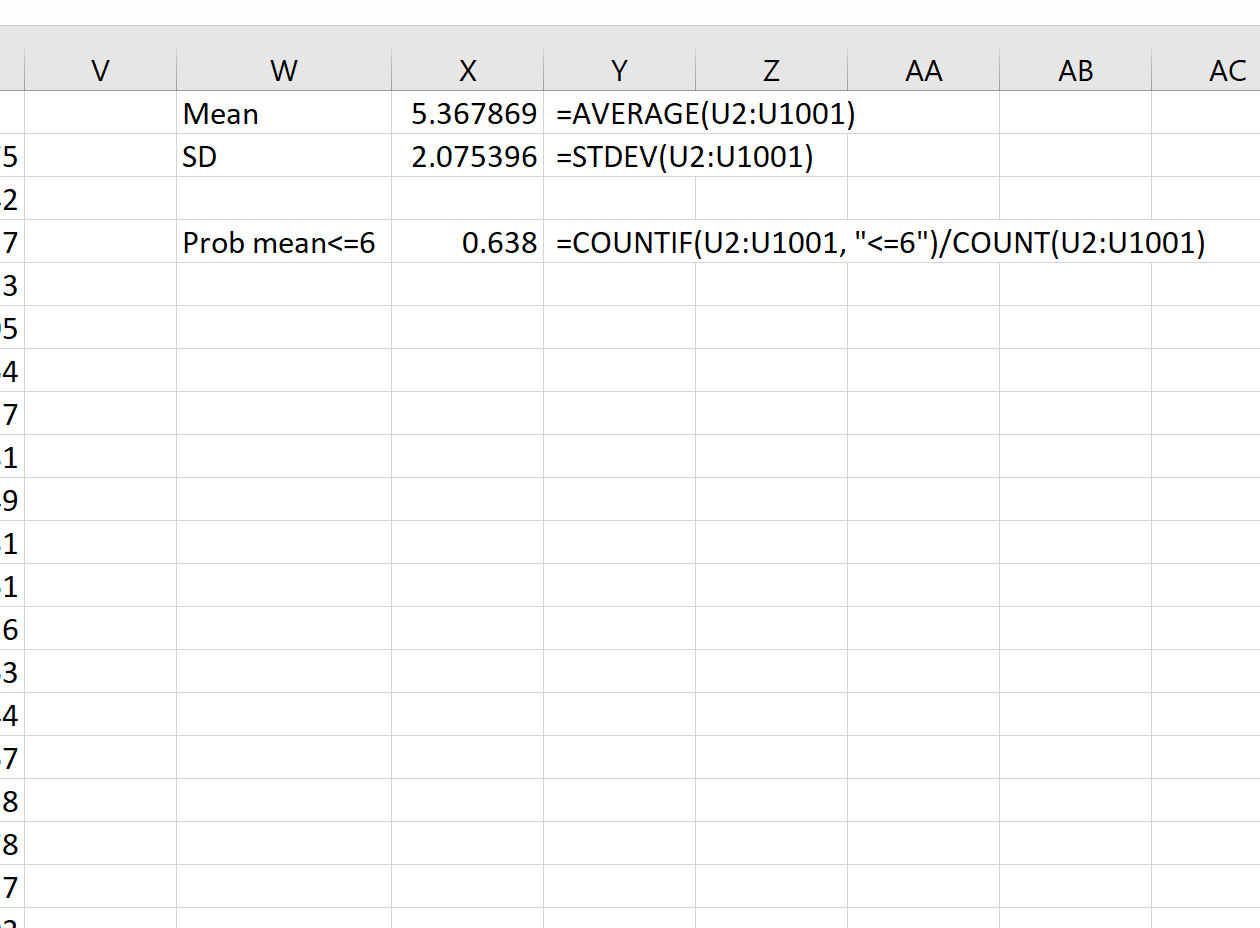
Мы видим, что вероятность того, что выборочное среднее меньше или равно 6, равна 0,638.

Это очень близко к вероятности, рассчитанной с помощью калькулятора выборочного распределения :

Дополнительные ресурсы

Введение в выборочные распределения
Калькулятор распределения выборки
Введение в центральную предельную теорему