Выборочное распределение доли

В этой статье объясняется, что такое выборочное распределение пропорций в статистике. Кроме того, вы найдете формулу пропорционального выборочного распределения и, кроме того, пошаговое решение упражнения.

Каково выборочное распределение пропорции?

Выборочное распределение пропорций (или выборочное распределение пропорций ) — это распределение, которое получается в результате расчета доли каждой возможной выборки из совокупности. То есть пропорции выборки всех возможных выборок из генеральной совокупности образуют выборочное распределение пропорций.

Другими словами, выборочное распределение пропорций получается путем изучения всех выборок, которые можно выбрать из генеральной совокупности, и определения выборочной доли каждой выборки. Таким образом, набор рассчитанных выборочных долей представляет собой выборочное распределение доли.

Если вам интересно, для чего предназначено выборочное распределение доли, в статистике оно используется для расчета вероятности приближения к значению доли населения при анализе одной выборки.

Формула пропорционального выборочного распределения

Фактически, когда мы изучаем часть выборки, мы анализируем случаи успеха. Таким образом, случайная величина в исследовании имеет биномиальное распределение вероятностей .

Согласно центральной предельной теореме, для больших размеров (n>30) мы можем приблизить биномиальное распределение к нормальному. Таким образом, выборочное распределение доли приближается к нормальному распределению со следующими параметрами:

Золото

это вероятность успеха и

это вероятность неудачи

.

Примечание. Биномиальное распределение можно приблизить к нормальному распределению только в том случае, если

И

.

Следовательно, поскольку выборочное распределение доли можно приблизить к нормальному распределению, формула для расчета любой вероятности, связанной с долей выборки, имеет следующий вид:

Золото:

• 

  – это доля выборки.

• 

  это доля населения.

• 

  — вероятность отказа популяции,

  

  .

• 

  это размер выборки.

• 

  — переменная, определяемая стандартным нормальным распределением N(0,1).

Конкретный пример пропорционального выборочного распределения

После того, как мы увидели определение пропорционального выборочного распределения и связанные с ним формулы, ниже приведен пошаговый пример решения, чтобы полностью понять концепцию.

• Промышленная компания закупает партии деталей у завода, который утверждает, что производит детали только с 3% бракованных деталей. Чтобы это проверить, компания решает проанализировать заказ на 500 деталей. Какова вероятность обнаружить в выборке более 5% бракованных деталей?

В этом случае доля популяции, которую мы хотим изучить, равна 0,03, поэтому параметр q эквивалентен 0,97.

Итак, чтобы найти вероятность того, что нас спросят, мы должны вычислить соответствующую статистику, применив формулу, которую мы видели в предыдущем разделе:

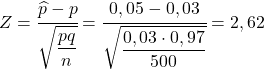
Таким образом, вероятность получения более 5% бракованных деталей эквивалентна следующей вероятности:

таблице распределения Z и вычисляем вероятность того, что задача задает нам:

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше