Распределение частоты

В этой статье объясняется, что такое частотное распределение и как оно достигается. Вы также найдете пошаговые примеры распределения частот и, кроме того, сможете попрактиковаться с решенными упражнениями.

Что такое частотное распределение?

В статистике распределение частот представляет собой таблицу, в которой различные значения выборки сгруппированы в строки и в каждом столбце отображается тип частоты каждого значения. Таким образом, распределение частот используется для отображения всех типов частот в наборе данных.

Более конкретно, частотное распределение включает в себя абсолютную частоту, совокупную абсолютную частоту, относительную частоту и совокупную относительную частоту.

Одной из характеристик частотных распределений является то, что они очень полезны для суммирования статистической выборки количественной переменной и качественной переменной.

Как сделать частотное распределение

Для выполнения частотного распределения необходимо выполнить следующие действия:

1. Организуйте данные по разным категориям и создайте таблицу, в которой каждая строка соответствует категории.
2. Рассчитайте абсолютную частоту каждой категории во втором столбце таблицы.
3. Рассчитайте совокупную абсолютную частоту каждой категории в третьем столбце таблицы.
4. Рассчитайте относительную частоту каждой категории в четвертом столбце таблицы.
5. Рассчитайте совокупную относительную частоту каждой категории в пятом столбце таблицы.
6. По желанию можно добавить два столбца, в которых относительная частота и накопительная относительная частота рассчитываются в процентах, для этого нужно просто умножить оба столбца на 100.

Пример распределения частот

После того, как мы ознакомились с определением частотного распределения и теорией его построения, в этом разделе шаг за шагом рассматривается пример.

• Оценки, полученные по предмету «Статистика» в классе из 30 учащихся, следующие. Постройте частотное распределение набора данных.

Поскольку все числа могут быть только целыми числами, это дискретная переменная. Поэтому нет необходимости группировать данные по интервалам.

Итак, чтобы составить частотное распределение, нам нужно построить таблицу, в которой каждое отдельное значение будет строкой, а затем нам нужно найти абсолютную частоту каждого значения:

Обратите внимание, что сумма всех абсолютных частот равна общему количеству данных. Если это правило не соблюдается, это означает, что вы забыли предоставить определенную информацию.

Теперь, когда мы знаем абсолютную частоту, нам нужно вычислить совокупную абсолютную частоту. Для этого расчета у нас есть два варианта: либо мы складываем абсолютную частоту значения плюс все абсолютные частоты наименьших значений, либо, наоборот, складываем абсолютную частоту значения плюс накопленную абсолютную частоту предыдущего значения.

Совокупная абсолютная частота последнего значения всегда соответствует общему количеству данных. Этот трюк можно использовать, чтобы убедиться в правильности расчетов.

Далее нам нужно определить относительную частоту, которая рассчитывается путем деления абсолютной частоты на общее количество точек данных (30):

Имейте в виду, что сумма всех относительных частот всегда равна 1, иначе это означает, что определенный расчет распределения частот неверен.

Наконец, нам просто нужно извлечь совокупную относительную частоту. Для этого необходимо сложить относительную частоту рассматриваемого значения плюс все предыдущие относительные частоты или, что то же самое, предыдущую накопленную относительную частоту:

Вкратце, частотное распределение со всеми частотами проблемных данных выглядит следующим образом:

Распределение частот для сгруппированных данных

Чтобы сделать частотное распределение для данных, сгруппированных по интервалам , единственное отличие состоит в том, что набор данных сначала нужно сгруппировать по разным интервалам, а остальные расчеты производятся так же, как и при частотном распределении без группировки данных.

В качестве примера ниже решается задача построения частотного распределения для сгруппированных данных.

• Был измерен рост 20 человек и получены результаты, указанные ниже. Создайте распределение частот, разделив данные на интервалы.

Данные в этом образце имеют непрерывное распределение, поскольку числа могут быть десятичными и, следовательно, принимать любое значение. Поэтому мы сделаем частотное распределение, сгруппировав данные по интервалам.

Хотя существует несколько математических правил создания интервалов выборки, в данном случае мы просто создадим интервалы шириной в 10 десятых.

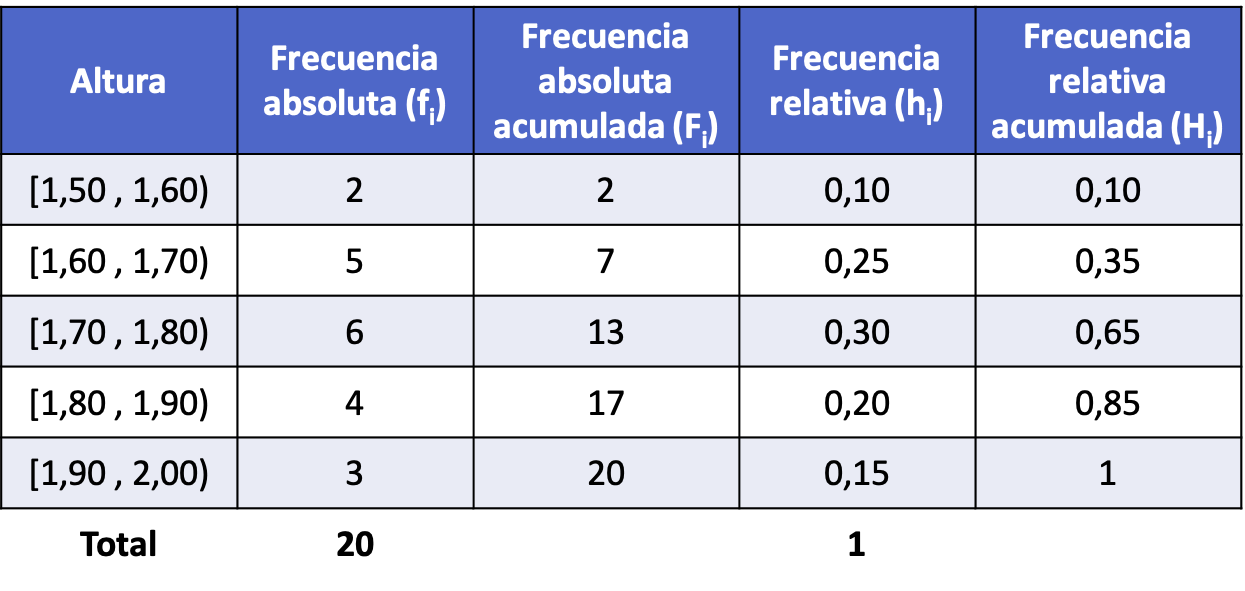
Итак, после расчета всех типов частот для каждого интервала (процедура такая же, как в примере выше), распределение частот с сгруппированными по интервалам данными выглядит следующим образом:

Решенные упражнения по распределению частот

Упражнение 1

Мы спросили 20 человек, сколько раз они ходят в кино в месяц, и вот результаты:

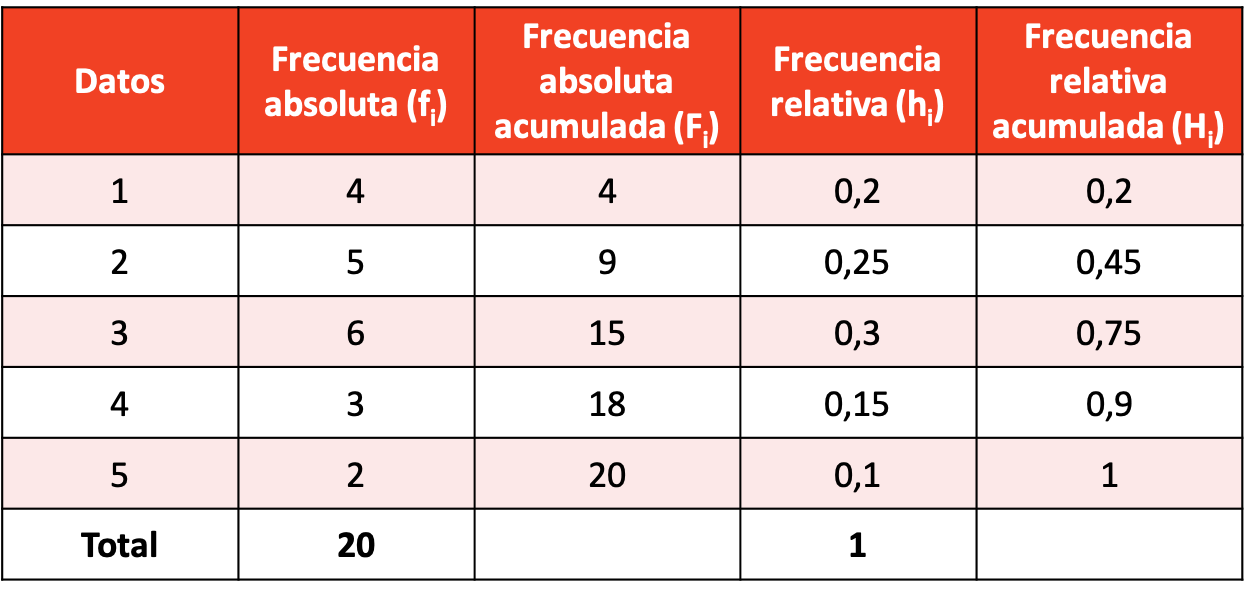
Сделайте частотное распределение с полученной выборкой данных.

Распределение частот с расчетами всех типов частот выглядит следующим образом:

Упражнение 2

Вы хотите провести статистическое исследование веса работников в компании с 36 сотрудниками. Вот вес рабочих, выраженный в килограммах:

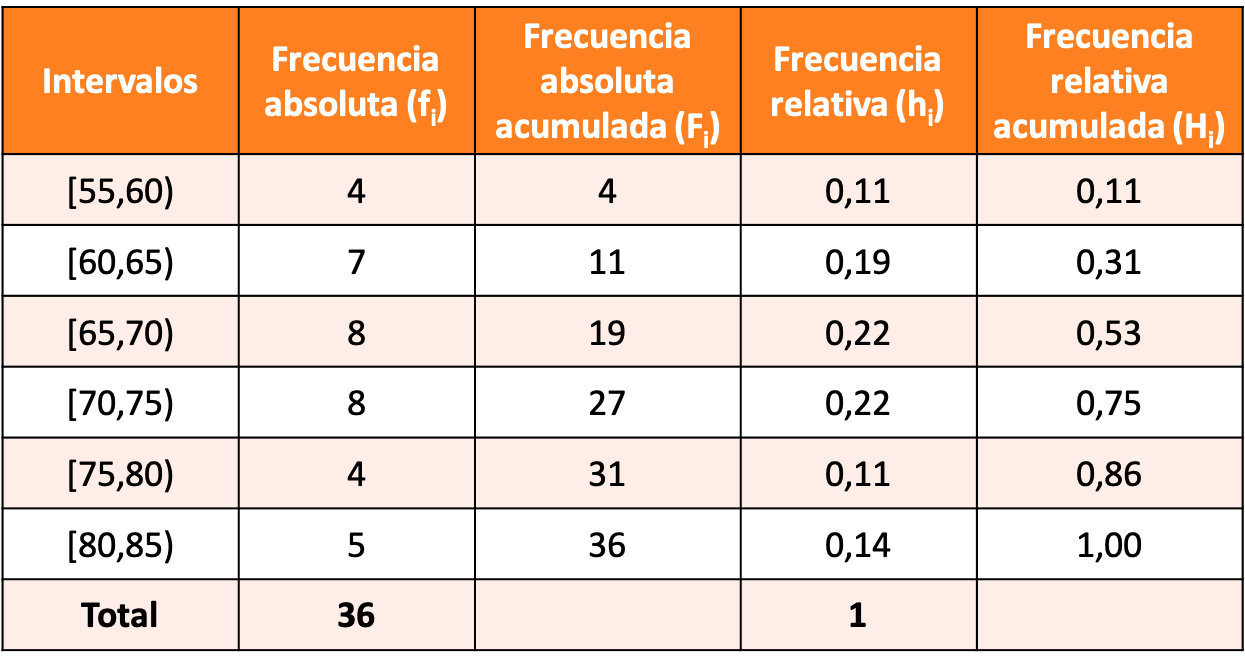
Постройте распределение частот с сгруппированными данными, сделав интервалы в 5 единиц, и пусть первый интервал будет [55,60).

Решением упражнения является следующее распределение частот: