Как рассчитать значения p в excel (3 примера)
В статистике мы используем проверку гипотез , чтобы определить, верно ли утверждение о параметре совокупности .
Когда мы проводим проверку гипотезы, нам часто дают статистику теста T-score.
Как только мы найдем эту статистику теста t-показателя, мы сможем найти связанное с ней значение p.
Если это значение p меньше определенного значения (например, 0,10, 0,05, 0,01), то мы отвергаем нулевую гипотезу теста и делаем вывод, что наши результаты статистически значимы.
В следующих примерах показано, как вычислить значение p для тестовой статистики в Excel в трех различных сценариях.
Пример 1. Вычисление значения P для двустороннего теста.
Предположим, ботаник хочет знать, равна ли средняя высота определенного вида растений 15 дюймам.
В случайной выборке из 12 растений она обнаружила, что средняя высота образца составляет 14,33 дюйма, а стандартное отклонение образца составляет 1,37 дюйма.
Он выполняет проверку гипотезы, используя следующие нулевые и альтернативные гипотезы:
H 0 (нулевая гипотеза): μ= 15 дюймов.
H A (альтернативная гипотеза): μ ≠ 15 дюймов.
Статистика теста рассчитывается следующим образом:
- т знак равно ( Икс – µ) / (s/ √n )
- т = (14,33-15) / (1,37/√ 12 )
- т = -1,694
Степени свободы, связанные с этой тестовой статистикой, равны n-1 = 12-1 = 11 .
Чтобы найти значение p для этой тестовой статистики, мы будем использовать следующую формулу в Excel:
=T.DIST.2T(ABS(-1.694), 11)
На следующем снимке экрана показано, как использовать эту формулу на практике.
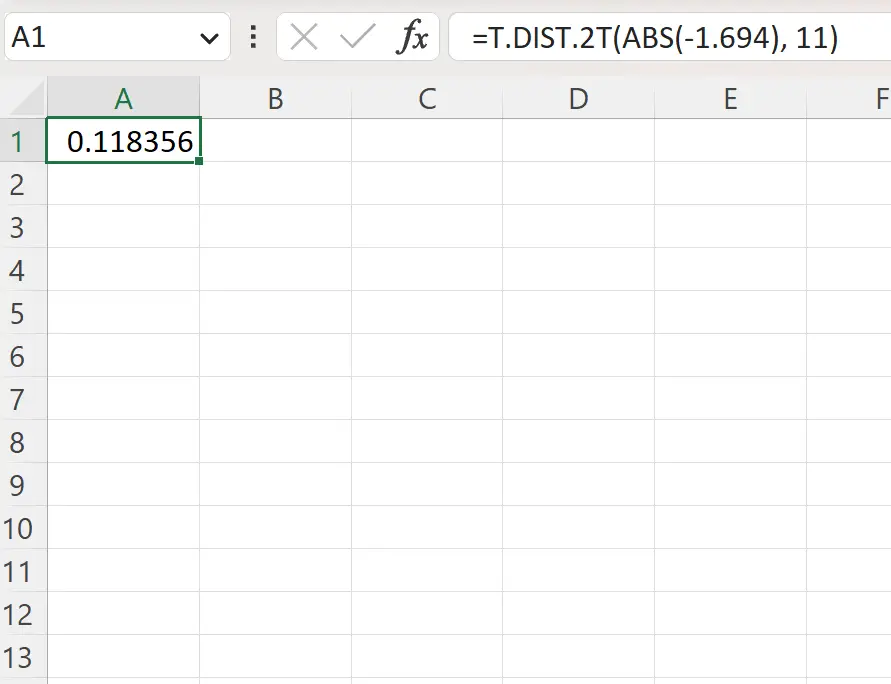
Двустороннее значение p составляет 0,1184 .
Поскольку это значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. У нас недостаточно доказательств, чтобы сказать, что средняя высота растения отличается от 15 дюймов.
Пример 2. Рассчитайте значение P для теста слева.
Допустим, мы предполагаем, что средний вес определенного гаджета, произведенного на заводе, составляет 20 грамм. Однако инспектор оценивает, что фактический средний вес составляет менее 20 граммов.
Чтобы проверить это, он взвешивает простую случайную выборку из 20 виджетов и получает следующую информацию:
- n = 20 виджетов
- х = 19,8 грамм
- с = 3,1 грамм
Затем он выполняет проверку гипотезы, используя следующие нулевые и альтернативные гипотезы:
H 0 (нулевая гипотеза): μ ≥ 20 граммов
H A (альтернативная гипотеза): μ < 20 граммов
Статистика теста рассчитывается следующим образом:
- т знак равно ( Икс – µ) / (s/ √n )
- т = (19,8-20) / (3,1/√ 20 )
- т = -.2885
Степени свободы, связанные с этой тестовой статистикой, равны n-1 = 20-1 = 19 .
Чтобы найти значение p для этой тестовой статистики, мы будем использовать следующую формулу в Excel:
=T.DIST(-.2885, 19, TRUE)
На следующем снимке экрана показано, как использовать эту формулу на практике.
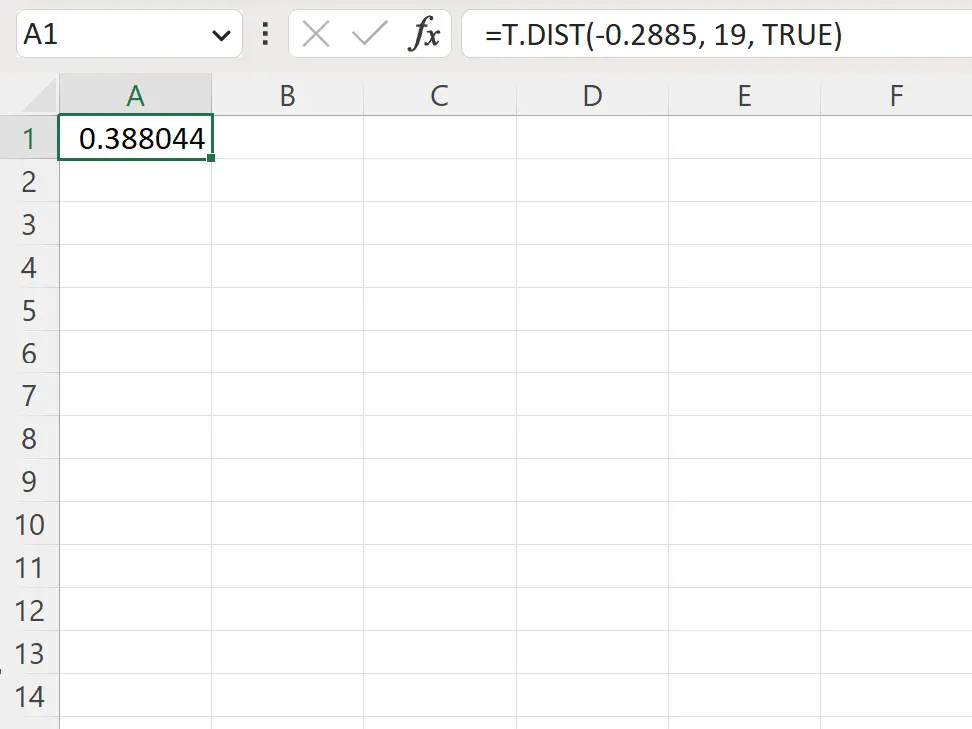
Значение p слева составляет 0,388044 .
Поскольку это значение не менее 0,05, инспектор не может отвергнуть нулевую гипотезу. Нет достаточных оснований утверждать, что реальный средний вес изделий, производимых на этом заводе, составляет менее 20 граммов.
Примечание . Мы использовали аргумент TRUE , чтобы указать, что при расчете значения p следует использовать кумулятивную функцию распределения.
Пример 3. Вычисление значения P для правостороннего критерия.
Предположим, что средняя высота определенного вида растений составляет 10 дюймов. Однако один ботаник говорит, что истинная средняя высота составляет более 10 дюймов.
Чтобы проверить это утверждение, она измеряет высоту простой случайной выборки из 15 растений и получает следующую информацию:
- n = 15 растений
- х = 11,4 дюйма
- с = 2,5 дюйма
Затем он выполняет проверку гипотезы, используя следующие нулевые и альтернативные гипотезы:
H 0 (нулевая гипотеза): μ ≤ 10 дюймов
H A (альтернативная гипотеза): μ > 10 дюймов.
Статистика теста рассчитывается следующим образом:
- т знак равно ( Икс – µ) / (s/ √n )
- т = (11,4-10) / (2,5/√ 15 )
- т = 2,1689
Степени свободы, связанные с этой статистикой теста, равны n-1 = 15-1 = 14 .
Чтобы найти значение p для этой тестовой статистики, мы будем использовать следующую формулу в Excel:
=T.DIST.RT(2.1689, 14)
На следующем снимке экрана показано, как использовать эту формулу на практике.
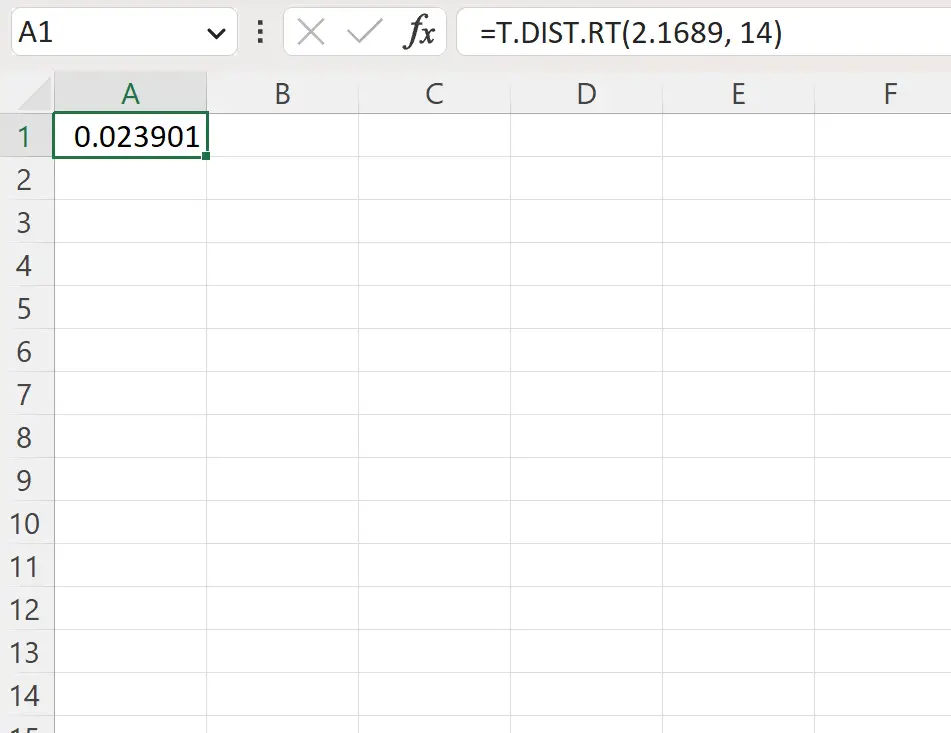
Значение p справа составляет 0,023901 .
Если это значение меньше 0,05, ботаник может отвергнуть нулевую гипотезу. У нее есть достаточно доказательств, чтобы сказать, что истинная средняя высота этого вида растений составляет более 10 дюймов.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как найти значение P по показателю Z в Excel
Как найти значение P статистики F в Excel
Как найти значение P статистики хи-квадрат в Excel