Регрессия через начало координат: определение и пример

Простая линейная регрессия — это метод, который можно использовать для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .

Простая модель линейной регрессии принимает следующую форму:

у = β ₀ + β ₁ х

Золото:

• y : значение переменной ответа
• β ₀ : значение переменной отклика при x = 0 (называемое термином «перехвата»).
• β ₁ : Среднее увеличение переменной ответа, связанное с увеличением x на одну единицу.
• x : значение прогнозируемой переменной.

Модифицированная версия этой модели известна как регрессия через начало координат , которая заставляет y быть равным 0, когда x равен 0.

Этот тип модели имеет следующую форму:

у = _β1x

Обратите внимание, что термин перехвата был полностью удален из модели.

Эта модель иногда используется, когда исследователи знают, что переменная ответа должна быть равна нулю, когда переменная-предиктор равна нулю.

В реальном мире модели этого типа чаще всего используются в лесных или экологических исследованиях .

Например, исследователи могут использовать окружность дерева для прогнозирования высоты дерева. Если данное дерево имеет нулевую длину окружности, оно должно иметь нулевую высоту.

Таким образом, при подгонке модели регрессии к этим данным не имеет смысла, чтобы исходный член был ненулевым.

В следующем примере показана разница между подгонкой обычной простой модели линейной регрессии и модели, реализующей регрессию через начало координат.

Пример: регрессия через начало координат

Предположим, биолог хочет подобрать регрессионную модель, используя окружность дерева, чтобы предсказать высоту дерева. Она выходит и собирает следующие измерения для выборки из 15 деревьев:

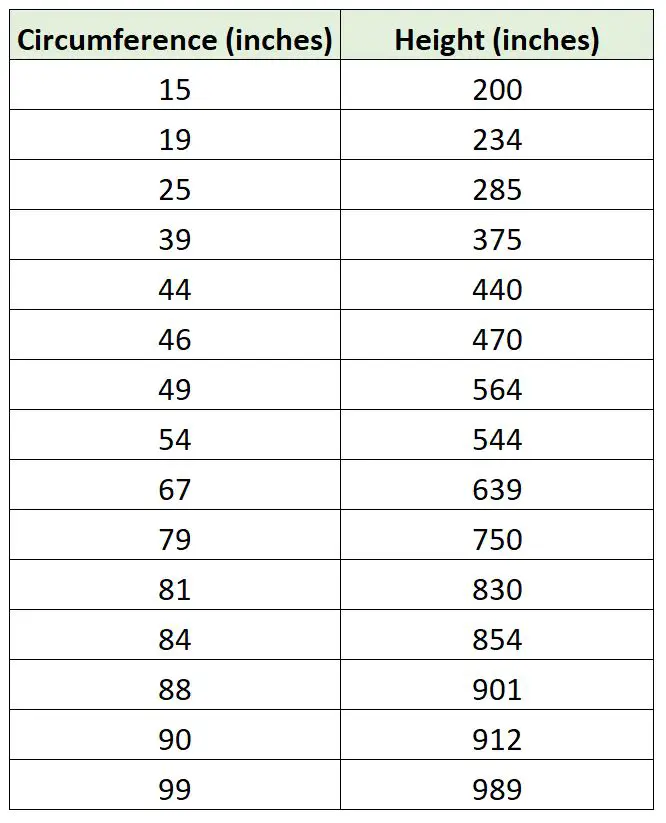
Мы можем использовать следующий код в R, чтобы согласовать простую модель линейной регрессии с моделью регрессии, которая не использует точки пересечения, и построить две линии регрессии:

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

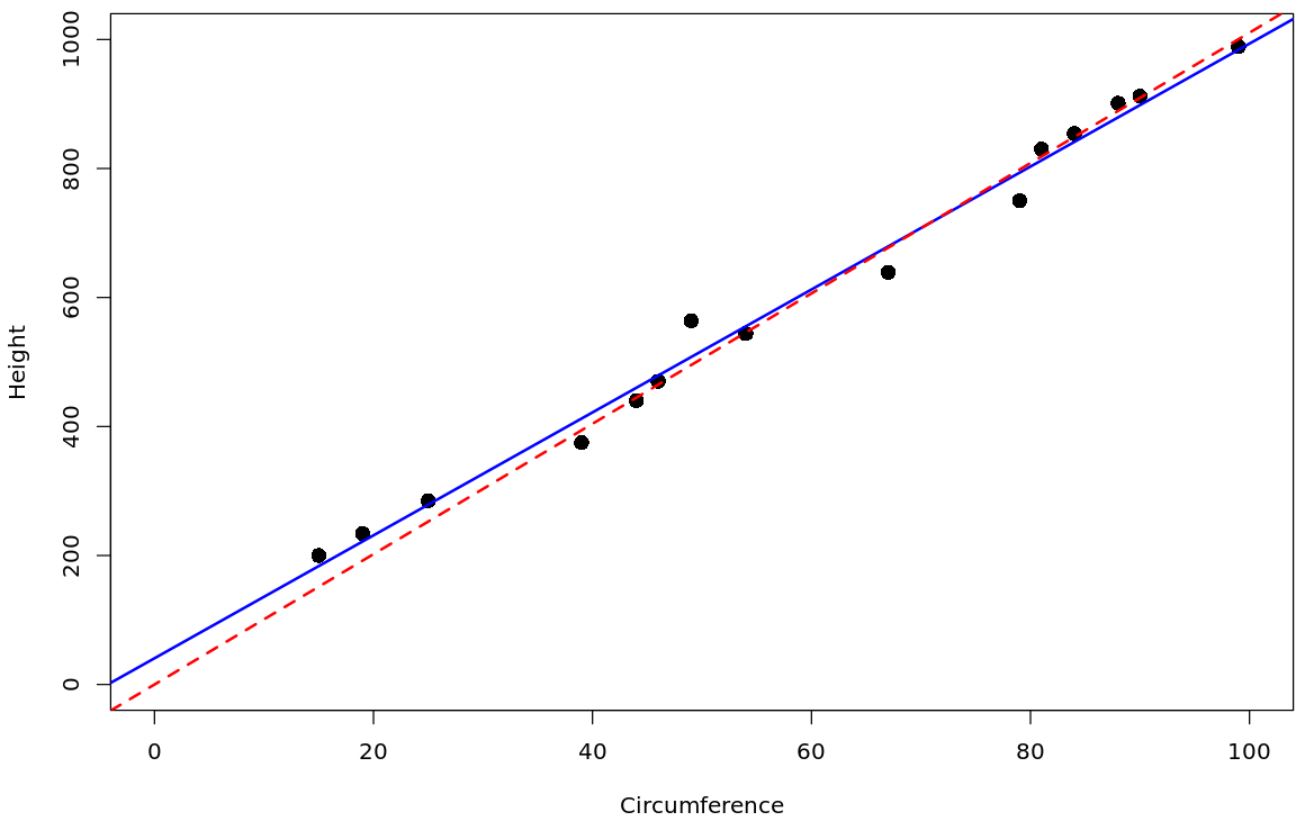
Красная пунктирная линия представляет модель регрессии, проходящую через начало координат, а синяя сплошная линия представляет собой обычную простую модель линейной регрессии.

Мы можем использовать следующий код в R для получения оценок коэффициентов для каждой модели:

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

Подогнанное уравнение для простой модели линейной регрессии:

Высота = 40,6969 + 9,5296 (окружность)

И подобранное уравнение для модели регрессии через начало координат:

Высота = 10,1057 (окружность)

Обратите внимание, что оценки коэффициента для переменной длины окружности немного отличаются.

Меры предосторожности при использовании регрессии через начало координат

Прежде чем использовать регрессию перехвата, вы должны быть абсолютно уверены, что значение 0 для переменной-предиктора подразумевает значение 0 для переменной ответа. Во многих сценариях почти невозможно узнать наверняка.

И если вы используете регрессию через начало координат, чтобы сохранить некоторую степень свободы в оценке начала координат, это редко имеет существенное значение, если размер вашей выборки достаточно велик.

Если вы решите использовать регрессию через начало координат, обязательно изложите свои рассуждения в окончательном анализе или отчете.

Дополнительные ресурсы

Следующие руководства предоставляют дополнительную информацию о линейной регрессии:

Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Как читать и интерпретировать таблицу регрессии