Регрессия главных компонентов в r (шаг за шагом)

Учитывая набор переменных-предикторов p и переменную отклика, множественная линейная регрессия использует метод, известный как наименьшие квадраты, для минимизации остаточной суммы квадратов (RSS):

RSS = Σ(y _i – ŷ _i ) ²

Золото:

• Σ : греческий символ, означающий сумму.
• y _i : фактическое значение ответа для ^i-го наблюдения
• ŷ _i : прогнозируемое значение ответа на основе модели множественной линейной регрессии.

Однако, когда переменные-предикторы сильно коррелируют, мультиколлинеарность может стать проблемой. Это может сделать оценки коэффициентов модели ненадежными и привести к высокой дисперсии.

Один из способов избежать этой проблемы — использовать регрессию главных компонентов , которая находит M линейных комбинаций (называемых «главными компонентами») исходных p- предикторов, а затем использует метод наименьших квадратов для подбора модели линейной регрессии с использованием главных компонентов в качестве предикторов.

В этом руководстве представлен пошаговый пример выполнения регрессии главных компонентов в R.

Шаг 1. Загрузите необходимые пакеты

Самый простой способ выполнить регрессию главных компонентов в R — использовать функции из пакета pls .

 #install pls package (if not already installed)
install.packages(" pls ")

load pls package
library(pls)

Шаг 2. Настройте модель ПЦР

В этом примере мы будем использовать встроенный набор данных R под названием mtcars , который содержит данные о различных типах автомобилей:

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

В этом примере мы подберем модель регрессии главных компонентов (PCR), используя hp в качестве переменной ответа и следующие переменные в качестве переменных-предикторов:

• миль на галлон
• отображать
• дерьмо
• масса
• qsec

Следующий код показывает, как подогнать модель PCR к этим данным. Обратите внимание на следующие аргументы:

• Scale=TRUE : это сообщает R, что каждая из переменных-предикторов должна быть масштабирована так, чтобы иметь среднее значение 0 и стандартное отклонение 1. Это гарантирует, что ни одна переменная-предиктор не будет иметь слишком большого влияния на модель, если она измеряется в разных единицах. .
• validation=”CV” : указывает R использовать k-кратную перекрестную проверку для оценки производительности модели. Обратите внимание, что по умолчанию используется k=10 складок. Также обратите внимание, что вместо этого вы можете указать «LOOCV», чтобы выполнить перекрестную проверку Leave-One-Out .

 #make this example reproducible
set.seed(1)

#fit PCR model
model <- pcr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")

Шаг 3: Выберите количество основных компонентов.

После того как мы скорректировали модель, нам нужно определить, сколько основных компонентов стоит сохранить.

Для этого просто посмотрите на среднеквадратическую ошибку теста (тест RMSE), рассчитанную с помощью проверки k-cross:

 #view summary of model fitting
summary(model)

Data: 
	Y dimension: 32 1
Fit method: svdpc
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 44.56 35.64 35.83 36.23 36.67
adjCV 69.66 44.44 35.27 35.43 35.80 36.20

TRAINING: % variance explained
    1 comp 2 comps 3 comps 4 comps 5 comps
X 69.83 89.35 95.88 98.96 100.00
hp 62.38 81.31 81.96 81.98 82.03

В результате получились две интересные таблицы:

1. ВАЛИДАЦИЯ: RMSEP

В этой таблице показан тест RMSE, рассчитанный путем перекрестной проверки в k-кратном размере. Мы можем увидеть следующее:

• Если мы используем только исходный термин в модели, RMSE теста составит 69,66 .
• Если мы добавим первый главный компонент, тест RMSE упадет до 44,56.
• Если мы добавим второй главный компонент, тест RMSE упадет до 35,64.

Мы видим, что добавление дополнительных главных компонентов фактически приводит к увеличению RMSE теста. Таким образом, представляется, что оптимально было бы использовать в итоговой модели только две главные компоненты.

2. ОБУЧЕНИЕ: объяснение % дисперсии

В этой таблице указан процент отклонения переменной отклика, объясняемый основными компонентами. Мы можем увидеть следующее:

• Используя только первый главный компонент, мы можем объяснить 69,83% вариаций переменной отклика.
• Добавляя второй главный компонент, мы можем объяснить 89,35% вариаций переменной отклика.

Обратите внимание, что мы по-прежнему сможем объяснить большую дисперсию, используя больше главных компонентов, но мы видим, что добавление более двух главных компонентов на самом деле не сильно увеличивает процент объясненной дисперсии.

Мы также можем визуализировать тест RMSE (наряду с тестом MSE и R-квадратом) как функцию количества главных компонентов, используя функцию validationplot() .

 #visualize cross-validation plots
validationplot(model)
validationplot(model, val.type="MSEP")
validationplot(model, val.type="R2") 

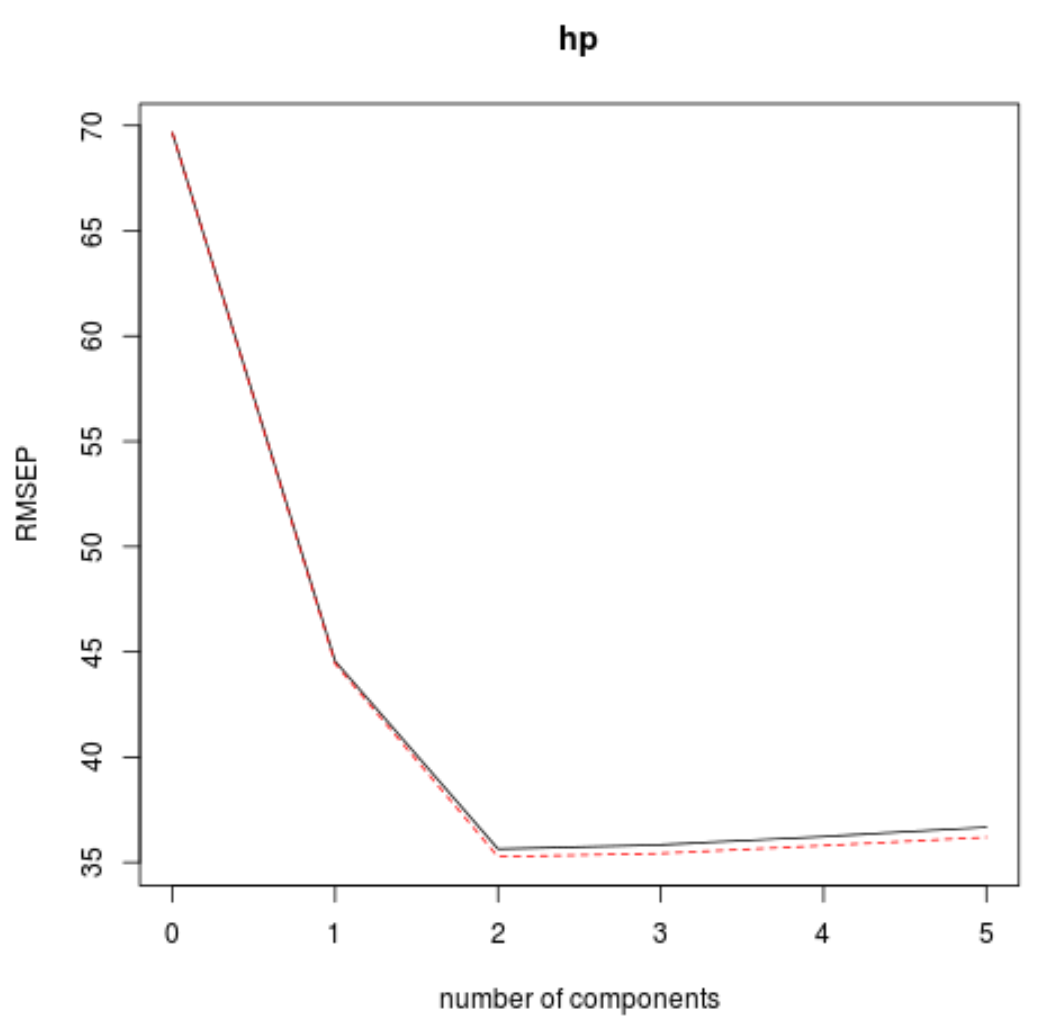
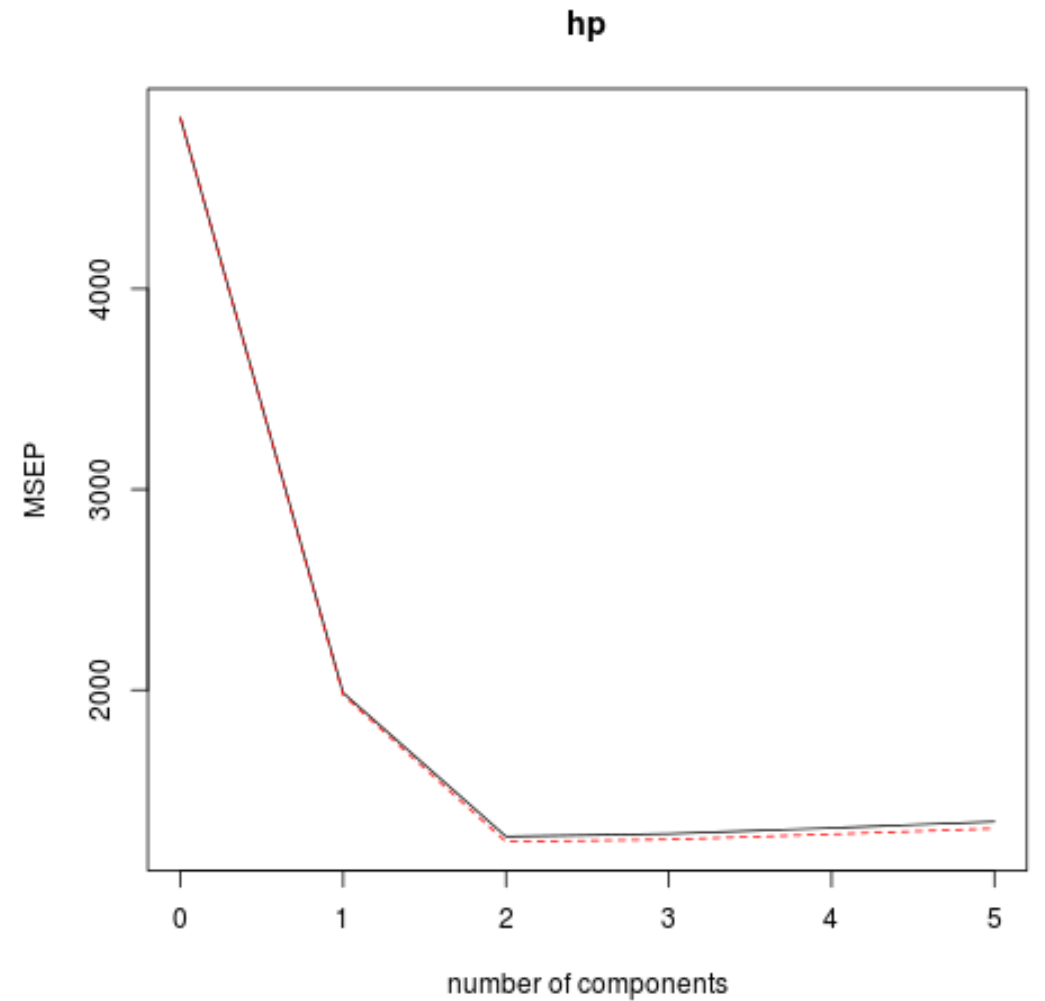
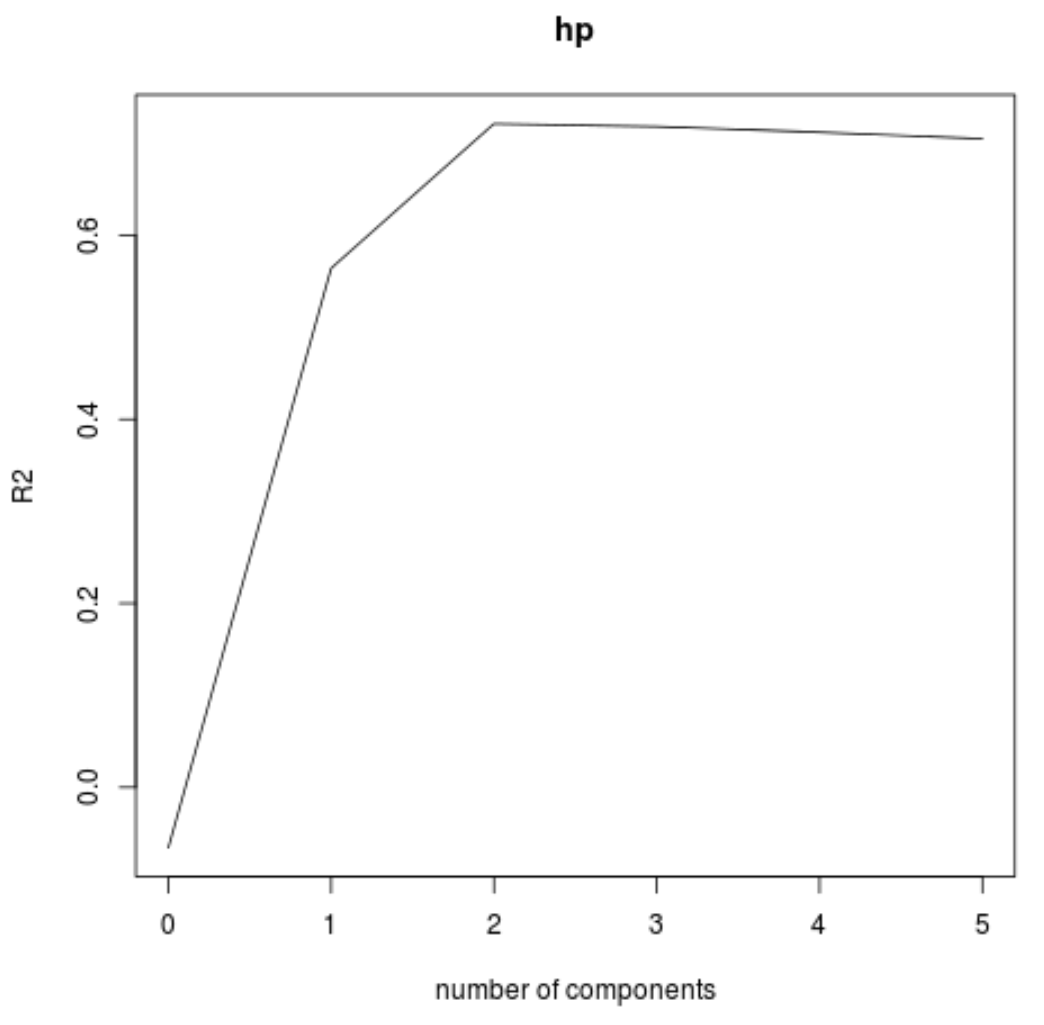
На каждом графике мы видим, что соответствие модели улучшается при добавлении двух главных компонентов, но имеет тенденцию ухудшаться при добавлении большего количества главных компонентов.

Таким образом, оптимальная модель включает только первые две главные компоненты.

Шаг 4. Используйте окончательную модель для прогнозирования

Мы можем использовать окончательную двухглавную модель ПЦР для прогнозирования новых наблюдений.

В следующем коде показано, как разделить исходный набор данных на обучающий и тестовый набор и использовать модель PCR с двумя основными компонентами для прогнозирования тестового набора.

 #define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26: nrow (mtcars), c("hp")]
test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- pcr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ")
pcr_pred <- predict(model, test, ncomp= 2 )

#calculate RMSE
sqrt ( mean ((pcr_pred - y_test)^2))

[1] 56.86549

Мы видим, что RMSE теста оказывается равным 56,86549 . Это среднее отклонение между прогнозируемым значением hp и наблюдаемым значением hp для наблюдений тестового набора.

Полное использование кода R в этом примере можно найти здесь .