Введение в ридж-регрессию

В обычной множественной линейной регрессии мы используем набор переменных-предикторов p и переменную отклика , чтобы соответствовать модели вида:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

Золото:

• Y : переменная ответа
• X _j : j- ^я прогнозируемая переменная
• β _j : Среднее влияние на Y увеличения X _j на одну единицу, при этом все остальные предикторы остаются фиксированными.
• ε : Погрешность

Значения β ₀ , β ₁ , B ₂ , …, β _p выбираются методом наименьших квадратов , который минимизирует сумму квадратов остатков (RSS):

RSS = Σ(y _i – ŷ _i ) ²

Золото:

• Σ : греческий символ, означающий сумму.
• y _i : фактическое значение ответа для ^i-го наблюдения
• ŷ _i : прогнозируемое значение ответа на основе модели множественной линейной регрессии.

Однако, когда переменные-предикторы сильно коррелируют, мультиколлинеарность может стать проблемой. Это может сделать оценки коэффициентов модели ненадежными и привести к высокой дисперсии.

Один из способов обойти эту проблему без полного удаления определенных переменных-предикторов из модели — использовать метод, известный как гребневая регрессия , который вместо этого стремится минимизировать следующее:

RSS + λΣβ _j ²

где j изменяется от 1 до p и λ ≥ 0.

Этот второй член в уравнении известен как штраф за снятие средств .

Когда λ = 0, этот штрафной член не имеет никакого эффекта, и гребневая регрессия дает те же оценки коэффициентов, что и метод наименьших квадратов. Однако по мере того, как λ приближается к бесконечности, штраф за усадку становится более влиятельным, и оценки пикового коэффициента регрессии приближаются к нулю.

В общем, наименее влиятельные переменные-предикторы в модели будут снижаться к нулю быстрее всего.

Зачем использовать ридж-регрессию?

Преимущество регрессии Риджа перед регрессией наименьших квадратов заключается в компромиссе между смещением и дисперсией .

Напомним, что среднеквадратическая ошибка (MSE) — это показатель, который мы можем использовать для измерения точности данной модели, и он рассчитывается следующим образом:

MSE = Var( f̂( x ₀ )) + [Смещение ( f̂( x ₀ ))] ² + Var(ε)

MSE = дисперсия + смещение ² + неустранимая ошибка

Основная идея регрессии Риджа состоит в том, чтобы ввести небольшое смещение, чтобы можно было значительно уменьшить дисперсию, что приведет к снижению общей MSE.

Чтобы проиллюстрировать это, рассмотрим следующий график:

Обратите внимание, что по мере увеличения λ дисперсия значительно уменьшается при очень небольшом увеличении смещения. Однако за определенной точкой дисперсия убывает медленнее и уменьшение коэффициентов приводит к их существенному занижению, что приводит к резкому увеличению систематической ошибки.

Из графика видно, что MSE теста является самым низким, когда мы выбираем значение λ, которое обеспечивает оптимальный компромисс между смещением и дисперсией.

Когда λ = 0, штрафной член в гребневой регрессии не оказывает никакого влияния и, следовательно, дает те же оценки коэффициентов, что и метод наименьших квадратов. Однако, увеличив λ до определенной точки, мы можем уменьшить общую MSE теста.

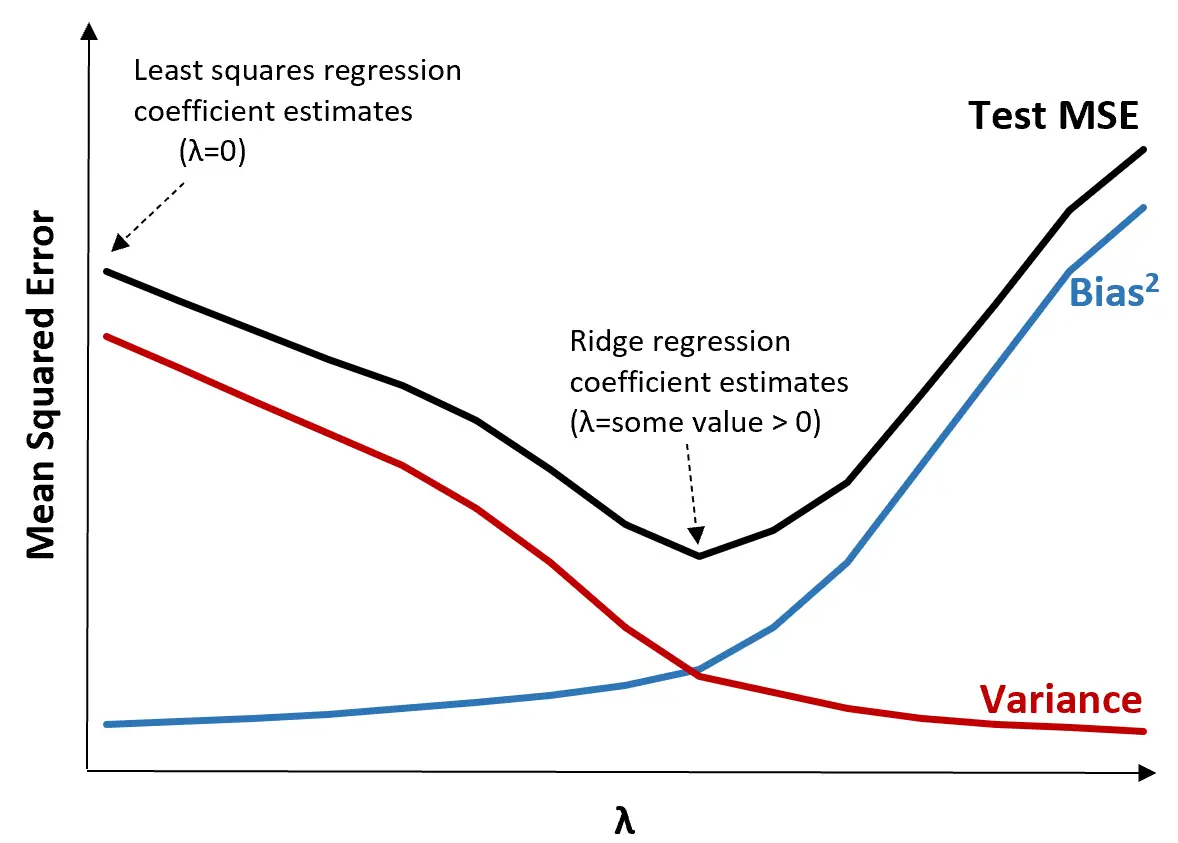
Это означает, что аппроксимация модели с помощью гребневой регрессии приведет к меньшим ошибкам теста, чем аппроксимация модели с помощью регрессии наименьших квадратов.

Шаги по выполнению гребневой регрессии на практике

Для выполнения гребневой регрессии можно использовать следующие шаги:

Шаг 1: Рассчитайте корреляционную матрицу и значения VIF для переменных-предикторов.

Во-первых, нам нужно создать корреляционную матрицу и рассчитать значения VIF (коэффициент инфляции дисперсии) для каждой переменной-предиктора.

Если мы обнаружим сильную корреляцию между переменными-предикторами и высокими значениями VIF (в некоторых текстах «высокое» значение VIF определяется как 5, а в других используется 10), то гребневая регрессия, вероятно, будет подходящей.

Однако, если в данных нет мультиколлинеарности, в первую очередь может не потребоваться выполнение гребневой регрессии. Вместо этого мы можем выполнить обычную регрессию по методу наименьших квадратов.

Шаг 2: Стандартизируйте каждую предикторную переменную.

Прежде чем выполнять гребневую регрессию, нам необходимо масштабировать данные таким образом, чтобы каждая переменная-предиктор имела среднее значение 0 и стандартное отклонение 1. Это гарантирует, что ни одна переменная-предиктор не будет иметь чрезмерного влияния при выполнении гребневой регрессии.

Шаг 3. Подберите модель гребневой регрессии и выберите значение λ.

Не существует точной формулы, которую мы могли бы использовать, чтобы определить, какое значение использовать для λ. На практике существует два распространенных способа выбора λ:

(1) Создайте график трассировки хребта. Это график, который визуализирует значения оценок коэффициентов при увеличении λ к бесконечности. Обычно мы выбираем λ как значение, при котором большинство оценок коэффициентов начинают стабилизироваться.

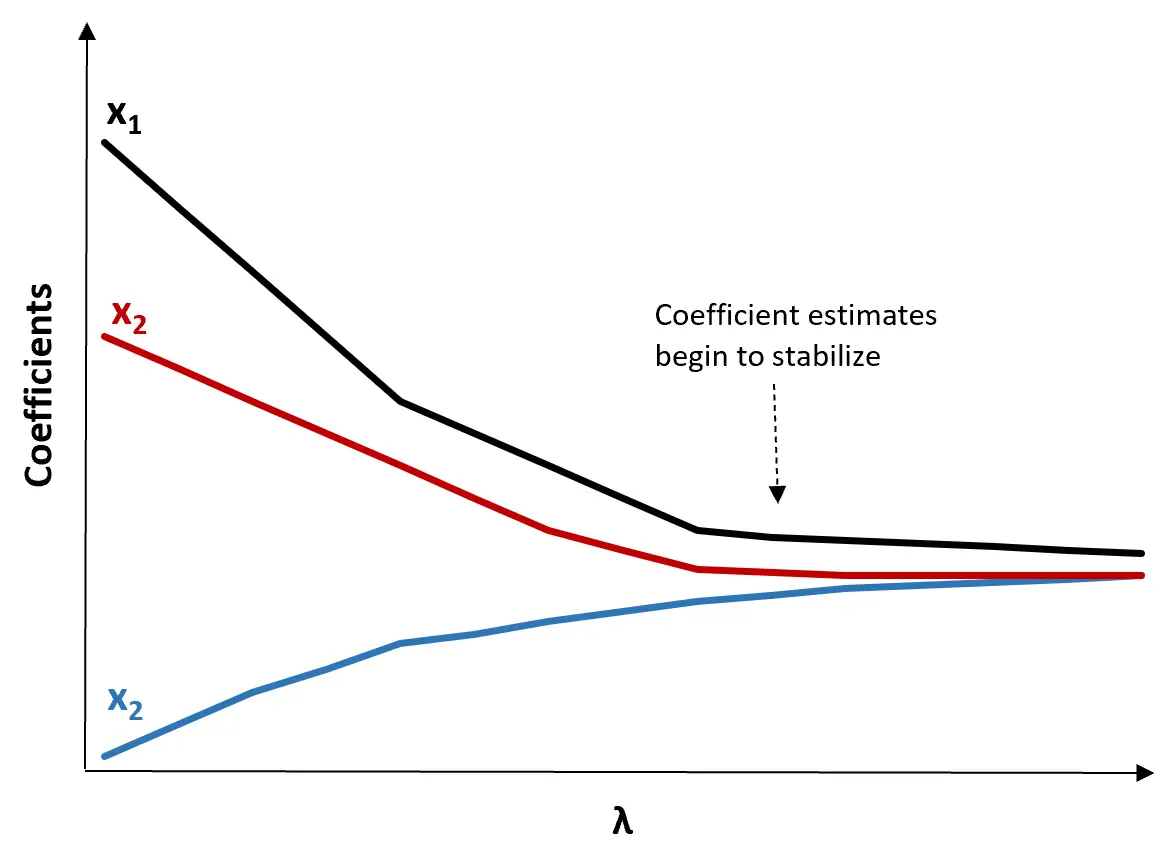
(2) Рассчитайте тест MSE для каждого значения λ.

Другой способ выбрать λ — просто вычислить тестовую MSE каждой модели с разными значениями λ и выбрать λ в качестве значения, которое дает наименьшую тестовую MSE.

Преимущества и недостатки ридж-регрессии

Самым большим преимуществом регрессии Риджа является ее способность давать меньшую среднеквадратическую ошибку (MSE), чем метод наименьших квадратов при наличии мультиколлинеарности.

Однако самым большим недостатком регрессии Риджа является ее неспособность выполнять выбор переменных, поскольку она включает все переменные-предикторы в окончательную модель. Поскольку некоторые предикторы будут уменьшены очень близко к нулю, это может затруднить интерпретацию результатов модели.

На практике регрессия Риджа имеет потенциал для создания модели, способной давать лучшие прогнозы по сравнению с моделью наименьших квадратов, но часто труднее интерпретировать результаты модели.

В зависимости от того, что для вас важнее: интерпретация модели или точность прогноза, вы можете использовать обычный метод наименьших квадратов или гребневую регрессию в разных сценариях.

Ридж-регрессия в R и Python

В следующих руководствах объясняется, как выполнить гребневую регрессию в R и Python, двух наиболее часто используемых языках для подбора моделей гребневой регрессии:

Ридж-регрессия в R (шаг за шагом)
Ридж-регрессия в Python (шаг за шагом)