Подгонка кривой в r (с примерами)
Часто вам может потребоваться найти уравнение, которое лучше всего описывает кривую R.

В следующем пошаговом примере объясняется, как подогнать кривые к данным в R с помощью функции poly() и как определить, какая кривая лучше всего соответствует данным.
Шаг 1. Создайте и визуализируйте данные
Давайте начнем с создания поддельного набора данных, а затем создадим диаграмму рассеяния для визуализации данных:
#create data frame df <- data. frame (x=1:15, y=c(3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46)) #create a scatterplot of x vs. y plot(df$x, df$y, pch= 19 , xlab=' x ', ylab=' y ')
Шаг 2. Отрегулируйте несколько кривых
Затем давайте адаптируем к данным несколько моделей полиномиальной регрессии и визуализируем кривую каждой модели на одном графике:
#fit polynomial regression models up to degree 5 fit1 <- lm(y~x, data=df) fit2 <- lm(y~poly(x,2,raw= TRUE ), data=df) fit3 <- lm(y~poly(x,3,raw= TRUE ), data=df) fit4 <- lm(y~poly(x,4,raw= TRUE ), data=df) fit5 <- lm(y~poly(x,5,raw= TRUE ), data=df) #create a scatterplot of x vs. y plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ') #define x-axis values x_axis <- seq(1, 15, length= 15 ) #add curve of each model to plot lines(x_axis, predict(fit1, data. frame (x=x_axis)), col=' green ') lines(x_axis, predict(fit2, data. frame (x=x_axis)), col=' red ') lines(x_axis, predict(fit3, data. frame (x=x_axis)), col=' purple ') lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ') lines(x_axis, predict(fit5, data. frame (x=x_axis)), col=' orange ')
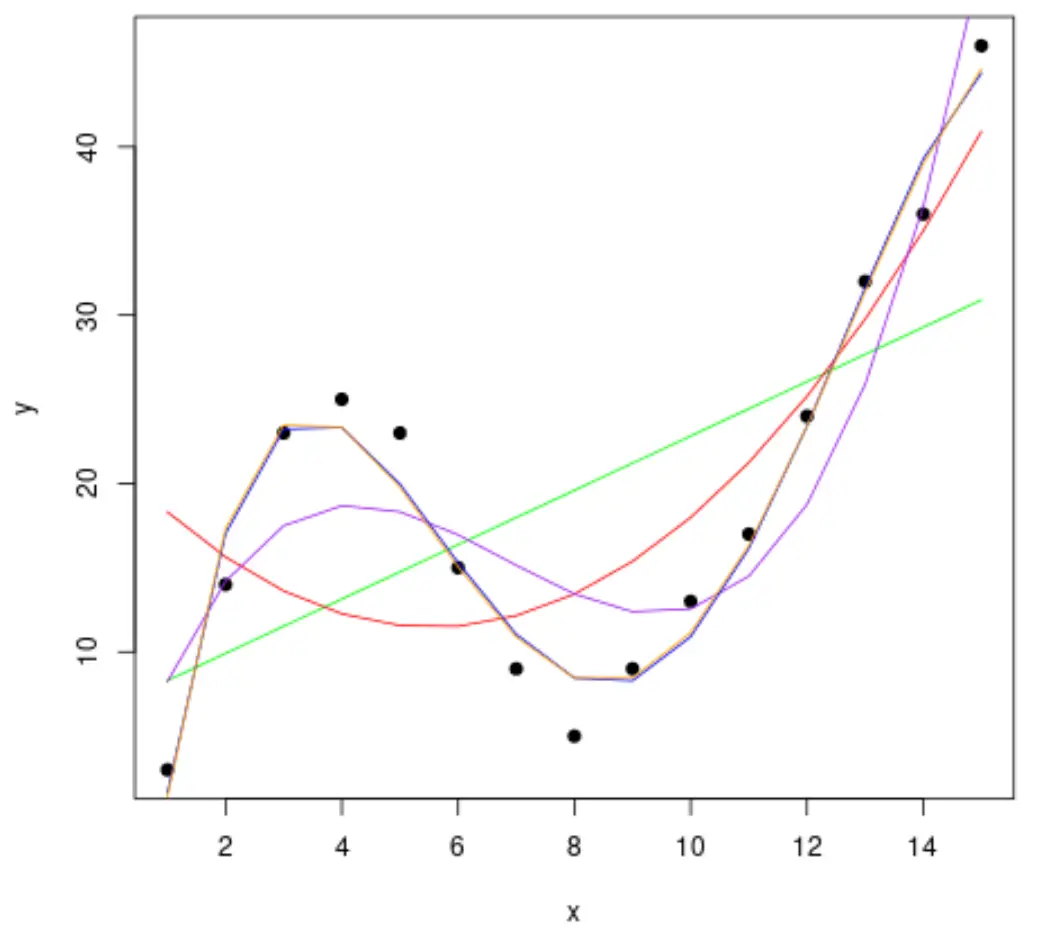
Чтобы определить, какая кривая лучше всего соответствует данным, мы можем посмотреть на скорректированный квадрат R каждой модели.
Это значение сообщает нам процент вариации переменной ответа, который можно объяснить переменными-предикторами в модели, с поправкой на количество переменных-предсказателей.
#calculated adjusted R-squared of each model summary(fit1)$adj. r . squared summary(fit2)$adj. r . squared summary(fit3)$adj. r . squared summary(fit4)$adj. r . squared summary(fit5)$adj. r . squared [1] 0.3144819 [1] 0.5186706 [1] 0.7842864 [1] 0.9590276 [1] 0.9549709
Из результата мы видим, что модель с самым высоким скорректированным R-квадратом представляет собой полином четвертой степени, который имеет скорректированный R-квадрат 0,959 .
Шаг 3: Визуализируйте окончательную кривую
Наконец, мы можем создать диаграмму рассеяния с кривой полиномиальной модели четвертой степени:
#create a scatterplot of x vs. y plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ') #define x-axis values x_axis <- seq(1, 15, length= 15 ) #add curve of fourth-degree polynomial model lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')

Мы также можем получить уравнение для этой строки, используя функцию summary() :
summary(fit4)
Call:
lm(formula = y ~ poly(x, 4, raw = TRUE), data = df)
Residuals:
Min 1Q Median 3Q Max
-3.4490 -1.1732 0.6023 1.4899 3.0351
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -26.51615 4.94555 -5.362 0.000318 ***
poly(x, 4, raw = TRUE)1 35.82311 3.98204 8.996 4.15e-06 ***
poly(x, 4, raw = TRUE)2 -8.36486 0.96791 -8.642 5.95e-06 ***
poly(x, 4, raw = TRUE)3 0.70812 0.08954 7.908 1.30e-05 ***
poly(x, 4, raw = TRUE)4 -0.01924 0.00278 -6.922 4.08e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.424 on 10 degrees of freedom
Multiple R-squared: 0.9707, Adjusted R-squared: 0.959
F-statistic: 82.92 on 4 and 10 DF, p-value: 1.257e-07
Уравнение кривой выглядит следующим образом:
у = -0,0192х 4 + 0,7081х 3 – 8,3649х 2 + 35,823х – 26,516
Мы можем использовать это уравнение для прогнозирования значения переменной отклика на основе переменных-предикторов в модели. Например, если x = 4, мы бы предсказали, что y = 23,34 :
у = -0,0192(4) 4 + 0,7081(4) 3 – 8,3649(4) 2 + 35,823(4) – 26,516 = 23,34
Дополнительные ресурсы
Введение в полиномиальную регрессию
Полиномиальная регрессия в R (шаг за шагом)
Как использовать функцию seq в R