Как найти режим сгруппированных данных: с примерами

Часто нам нужно рассчитать, каким образом данные сгруппированы.

Помните, что режим представляет значение, которое появляется чаще всего.

Например, предположим, что у нас есть следующие сгруппированные данные:

Хотя рассчитать точный режим невозможно, поскольку мы не знаем исходных значений данных , его можно оценить, используя следующую формулу:

Режим сгруппированных данных = L + W[(F _m – F ₁ )/( (F _m -F ₁ ) + (F _m – F ₂ ) )]

Золото:

• L : Нижний предел модального класса.
• W : Ширина модального класса.
• F _m : Частота модального класса
• F ₁ : Частота прохождения курса непосредственно перед модальным курсом.
• F ₂ : Частота курсов сразу после модального курса.

Примечание . Модальный класс — это просто класс с самой высокой частотой. В приведенном выше примере модальный класс будет 21–30, поскольку он имеет самую высокую частоту.

В следующих примерах показано, как рассчитать режим сгруппированных данных в различных сценариях.

Пример 1: Расчет режима сгруппированных данных

Предположим, у нас есть следующее распределение частот, показывающее, что экзамен оценили 40 учеников определенного класса:

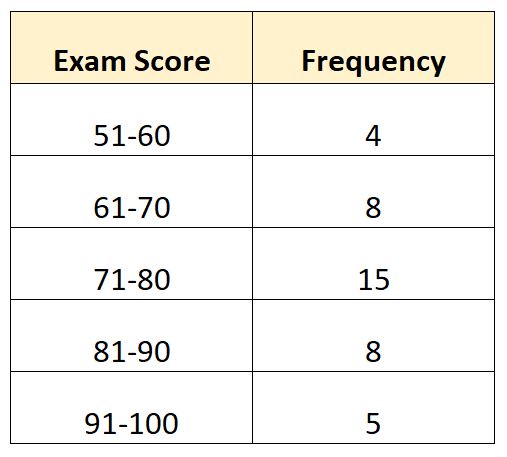
В этом примере модальный класс — 71-80.

Зная это, мы можем рассчитать следующие значения:

• L : Нижний предел модального класса: 71.
• W : Ширина модального класса: 9.
• F _m : Частота модального класса: 15
• F ₁ : Частота прохождения курса непосредственно перед модальным курсом: 8.
• F ₂ : Частота прохождения курса сразу после модального курса: 8

Мы можем подставить эти значения в формулу для расчета режима распределения:

• Режим = L + W[(F _m – F ₁ )/( (F _m -F ₁ ) + (F _m – F ₂ ) )]
• Режим = 71 + 9[(15-8) / ( (15-8) + (15-8) )]
• Режим = 75,5

Мы оцениваем балл модального экзамена в 75,5 .

Пример 2. Расчет режима сгруппированных данных

Предположим, у нас есть следующее частотное распределение, показывающее количество очков, набранных за игру 60 баскетболистами:

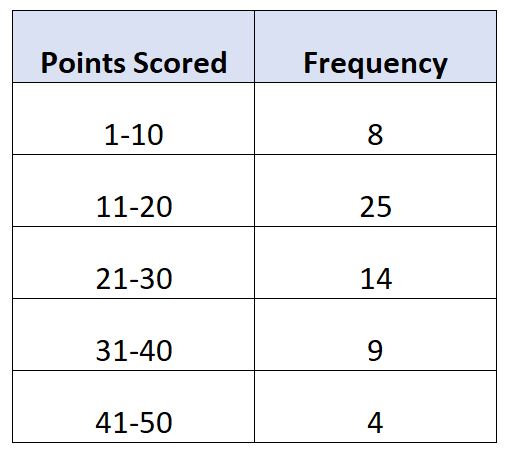
В этом примере модальный класс — 11-20.

Зная это, мы можем рассчитать следующие значения:

• L : Нижний предел модального класса: 11.
• W : Ширина модального класса: 9.
• F _m : Частота модального класса: 25
• F ₁ : Частота прохождения курса непосредственно перед модальным курсом: 8.
• F ₂ : Частота курсов сразу после модального курса: 14.

Мы можем подставить эти значения в формулу для расчета режима распределения:

• Режим = L + W[(F _m – F ₁ )/( (F _m -F ₁ ) + (F _m – F ₂ ) )]
• Режим = 11 + 9[(25-8) / ( (25-8) + (25-14) )]
• Мода = 16,46

По нашим оценкам, количество набранных модальных баллов составляет 16,46 .

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные операции с сгруппированными данными:

Как найти среднее и стандартное отклонение сгруппированных данных
Как найти медиану сгруппированных данных
Как рассчитать процентильный рейтинг для сгруппированных данных