Как выполнить тест крускала-уоллиса в stata

Тест Крускала-Уоллиса используется для определения наличия или отсутствия статистически значимой разницы между медианами трех или более независимых групп. Он считается непараметрическим эквивалентом однофакторного дисперсионного анализа .

В этом руководстве объясняется, как выполнить тест Крускала-Уоллиса в Stata.

Как выполнить тест Крускала-Уоллиса в Stata

В этом примере мы будем использовать набор данных переписи населения , который содержит данные переписи 1980 года для всех пятидесяти штатов США. В наборе данных штаты разделены на четыре различных региона:

• Норд Эст
• Северный Центральный
• Юг
• Запад

Мы проведем тест Крускала-Уоллиса, чтобы определить, равен ли средний возраст в этих четырех регионах.

Шаг 1: Загрузите и отобразите данные.

Сначала загрузите набор данных, введя следующую команду в поле «Команда»:

используйте https://www.stata-press.com/data/r13/census

Получите краткую сводку набора данных, используя следующую команду:

обобщить

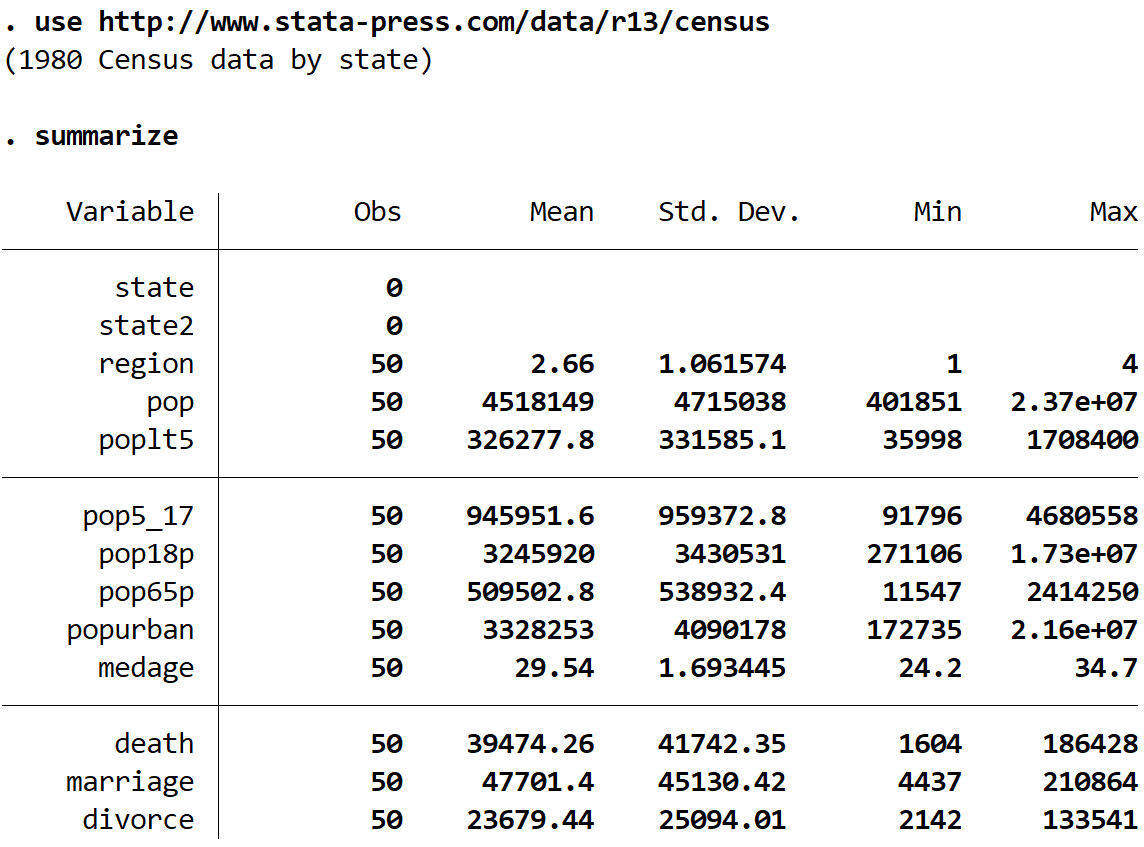
Мы видим, что в этом наборе данных есть 13 различных переменных, но мы будем работать только с двумя — это medage (средний возраст) и регион .

Шаг 2: Визуализируйте данные.

Прежде чем выполнять тест Крускала-Уоллиса, давайте сначала создадим несколько коробчатых диаграмм , чтобы визуализировать медианное возрастное распределение для каждого из четырех регионов:

Графическое поле медирования, вкл. (регион)

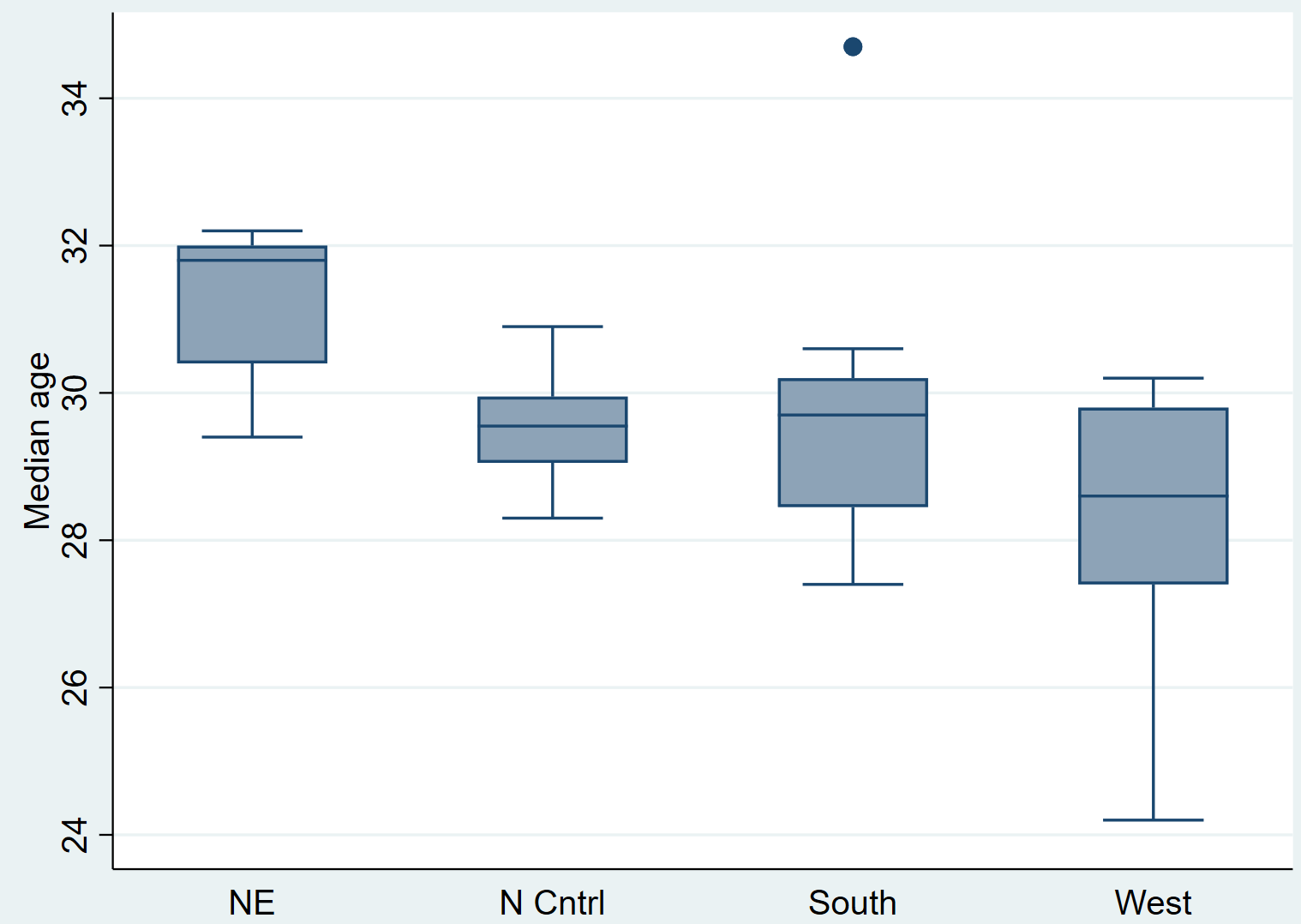
Просто взглянув на коробчатые диаграммы, можно увидеть, что распределение варьируется от региона к региону. Затем мы проведем тест Крускала-Уоллиса, чтобы проверить, являются ли эти различия статистически значимыми.

Шаг 3: Выполните тест Крускала-Уоллиса.

Используйте следующий синтаксис для выполнения теста Крускала-Уоллиса:

kwallis Measure_variable, по (grouping_variable)

В нашем случае мы будем использовать следующий синтаксис:

Кваллис Медадж, автор (регион)

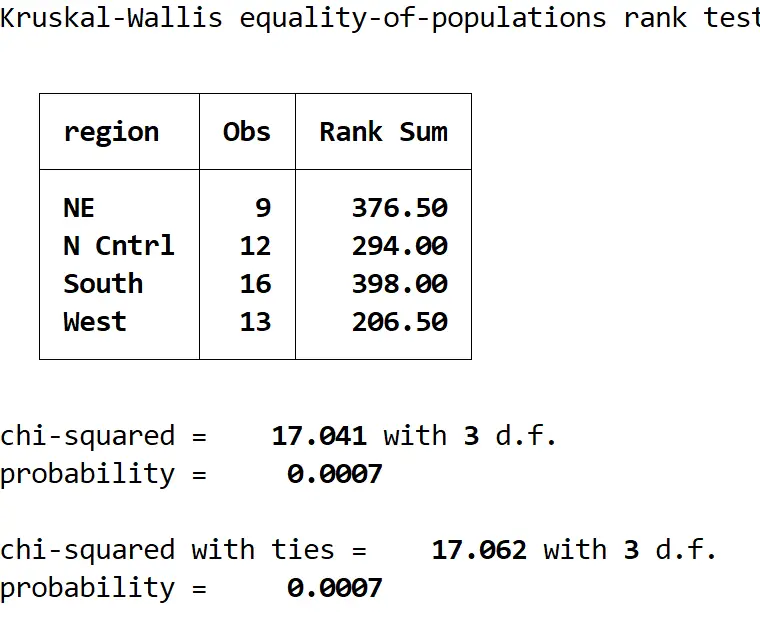
Вот как интерпретировать результат:

Сводная таблица: В этой таблице показано количество наблюдений по регионам и суммы рейтингов для каждого региона.

Хи-квадрат со связями: это значение тестовой статистики, которое оказывается равным 17,062.

вероятность: это значение p, соответствующее тестовой статистике, которая оказывается равной 0,0007. Поскольку это значение меньше 0,05, мы можем отвергнуть нулевую гипотезу и сделать вывод, что средний возраст не одинаков в четырех регионах.

Шаг 4: Сообщите о результатах.

Наконец, мы хотели бы сообщить о результатах теста Крускала-Уоллиса. Вот пример того, как это сделать:

Тест Крускала-Уоллиста был проведен, чтобы определить, был ли средний возраст людей одинаковым в следующих четырех регионах Соединенных Штатов:

• Северо-восток (n=9)
• Северо-Центральный (n=12)
• Юг (n=16)
• Запад (n=13)

Тест показал, что средний возраст людей не был одинаковым (X ² = 17,062, p = 0,0007) в четырех регионах. То есть существовала статистически значимая разница в среднем возрасте между двумя или более регионами.