Скорректированное отношение шансов: определение + примеры
В статистике отношение шансов показывает нам соотношение между вероятностью события, произошедшего в экспериментальной группе, и вероятностью события, произошедшего в контрольной группе.
Отношения шансов чаще всего появляются в логистической регрессии — методе, который мы используем для подбора модели регрессии, имеющей одну или несколько переменных-предикторов и переменную двоичного отклика.
Скорректированное отношение шансов — это отношение шансов, скорректированное с учетом других переменных-предикторов в модели.
Это особенно полезно, помогая нам понять, как переменная-предиктор влияет на вероятность возникновения события после поправки на влияние других переменных-предсказателей.
Следующий пример иллюстрирует разницу между отношением шансов и скорректированным отношением шансов.
Пример: расчет скорректированных коэффициентов шансов
Предположим, мы хотим понять, влияет ли возраст матери на вероятность рождения ребенка с низкой массой тела при рождении.
Чтобы изучить это, мы можем выполнить логистическую регрессию, используя возраст в качестве предикторной переменной и низкий вес при рождении (да или нет) в качестве переменной ответа .
Предположим, мы собираем данные о 300 матерях и подбираем модель логистической регрессии. Вот результаты:
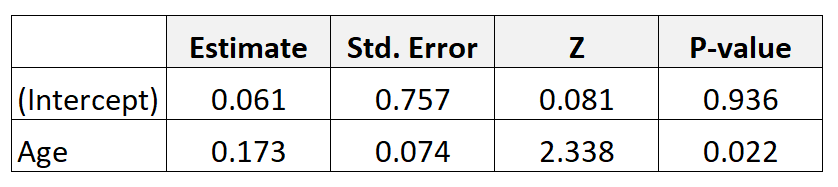
Чтобы получить отношение шансов для возраста, просто возведите в степень оценку коэффициента из таблицы: e 0,173 = 1,189 .
Это говорит нам о том, что увеличение возраста на один год связано с увеличением в 1189 раз вероятности рождения ребенка с низким весом. Другими словами, шансы родить ребенка с низкой массой тела при рождении увеличиваются на 18,9% с каждым дополнительным ежегодным увеличением возраста.
Это отношение шансов называется «грубым» отношением шансов или «нескорректированным» отношением шансов, поскольку оно не было скорректировано с учетом других переменных-предикторов в модели, поскольку это единственная переменная-предиктор в модели.
Но предположим, что мы хотим понять, влияют ли возраст матери и привычка курить на вероятность рождения ребенка с низким весом при рождении.
Чтобы изучить это, мы можем выполнить логистическую регрессию, используя возраст и курение (да или нет) в качестве переменных-предсказателей и низкий вес при рождении в качестве переменной ответа .
Предположим, мы собираем данные о 300 матерях и подбираем модель логистической регрессии. Вот результаты:
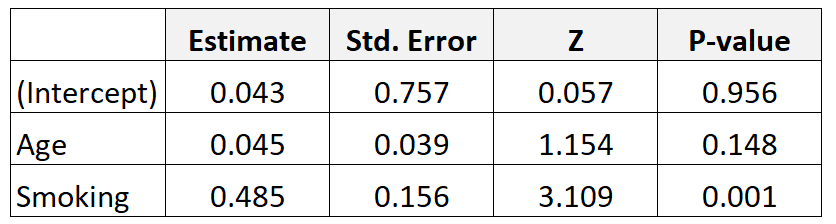
Вот как интерпретировать результаты:
Возраст: Отношение шансов с поправкой на возраст рассчитывается следующим образом: e 0,045 = 1,046 . Это означает, что шансы родить ребенка с низкой массой тела при рождении увеличиваются на 4,6% с каждым дополнительным ежегодным увеличением возраста, при условии, что переменная курения остается постоянной.
Например, предположим, что Мать А и Мать Б курят. Если мать А на год старше матери Б, то вероятность того, что у матери А родится ребенок с низкой массой тела, в 1,046 раза превышает вероятность того, что у матери Б родится ребенок с низкой массой тела.
Курение : Скорректированное отношение шансов для курения рассчитывается следующим образом: e.485 = 1,624 . Это означает, что шансы родить ребенка с низкой массой тела при рождении увеличиваются на 62,4%, если мать курит (по сравнению с некурящей), при условии, что возрастная переменная остается постоянной.
Например, предположим, что матери А и матери Б по 30 лет. Если мать А курит во время беременности, а мать Б не курит, то шансы у матери А родить ребенка с низкой массой тела на 62,4% выше, чем шансы у матери Б родить ребенка с низкой массой тела.
Обратите внимание, что отношение шансов с поправкой на возраст ниже, чем отношение шансов без поправки из предыдущего примера. Это связано с тем, что, когда другие переменные-предикторы увеличивают вероятность появления переменной ответа, скорректированное отношение шансов для переменной-предиктора, уже присутствующей в модели, всегда будет уменьшаться.
Резюме: отношение шансов против скорректированного отношения шансов
Отношение шансов (иногда называемое «грубым» отношением шансов) полезно для того, чтобы рассказать нам, как изменения в переменной-предикторе влияют на вероятность возникновения переменной отклика.
Скорректированное отношение шансов полезно для того, чтобы рассказать нам, как изменения в переменной-предикторе влияют на вероятность возникновения переменной-ответа после контроля других переменных-предикторов в модели.
Дополнительные ресурсы
Введение в логистическую регрессию
Как выполнить логистическую регрессию в R
Как выполнить логистическую регрессию в Python