Как создать случайные леса в r (шаг за шагом)
Когда взаимосвязь между набором переменных-предикторов и переменной отклика очень сложна, мы часто используем нелинейные методы для моделирования взаимосвязи между ними.
Одним из таких методов является построение дерева решений . Однако недостатком использования единого дерева решений является то, что оно склонно к высокой дисперсии .
То есть, если мы разделим набор данных на две половины и применим дерево решений к обеим половинам, результаты могут сильно отличаться.
Один из методов, который мы можем использовать для уменьшения дисперсии одного дерева решений, — это построение модели случайного леса , которая работает следующим образом:
1. Возьмите b самозагружаемых выборок из исходного набора данных.
2. Создайте дерево решений для каждого образца начальной загрузки.
- При построении дерева каждый раз, когда рассматривается разделение, только случайная выборка из m предикторов считается кандидатами на расщепление из полного набора p предикторов. Обычно мы выбираем m равным √p .
3. Усредните прогнозы каждого дерева, чтобы получить окончательную модель.
Оказывается, что случайные леса имеют тенденцию создавать гораздо более точные модели, чем одиночные деревья решений и даже пакетные модели .
В этом руководстве представлен пошаговый пример создания модели случайного леса для набора данных в R.
Шаг 1. Загрузите необходимые пакеты
Сначала мы загрузим необходимые пакеты для этого примера. Для этого простого примера нам нужен только один пакет:
library (randomForest)
Шаг 2. Настройте модель случайного леса
В этом примере мы будем использовать встроенный набор данных R под названием « Качество воздуха» , который содержит измерения качества воздуха в Нью-Йорке за 153 отдельных дня.
#view structure of air quality dataset str(airquality) 'data.frame': 153 obs. of 6 variables: $ Ozone: int 41 36 12 18 NA 28 23 19 8 NA ... $Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ... $ Wind: num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ... $ Temp: int 67 72 74 62 56 66 65 59 61 69 ... $Month: int 5 5 5 5 5 5 5 5 5 5 ... $Day: int 1 2 3 4 5 6 7 8 9 10 ... #find number of rows with missing values sum(! complete . cases (airquality)) [1] 42
Этот набор данных содержит 42 строки с пропущенными значениями. Поэтому перед подгонкой модели случайного леса мы заполним недостающие значения в каждом столбце медианами столбца:
#replace NAs with column medians for (i in 1: ncol (air quality)) { airquality[,i][ is . na (airquality[, i])] <- median (airquality[, i], na . rm = TRUE ) }
Связанный: Как вменить пропущенные значения в R
Следующий код показывает, как подогнать модель случайного леса в R с помощью функции randomForest() из пакета randomForest .
#make this example reproducible set.seed(1) #fit the random forest model model <- randomForest( formula = Ozone ~ ., data = airquality ) #display fitted model model Call: randomForest(formula = Ozone ~ ., data = airquality) Type of random forest: regression Number of trees: 500 No. of variables tried at each split: 1 Mean of squared residuals: 327.0914 % Var explained: 61 #find number of trees that produce lowest test MSE which.min(model$mse) [1] 82 #find RMSE of best model sqrt(model$mse[ which . min (model$mse)]) [1] 17.64392
Из результата мы видим, что модель, которая произвела наименьшую среднеквадратическую ошибку теста (MSE), использовала 82 дерева.
Мы также видим, что среднеквадратическая ошибка этой модели составила 17,64392 . Мы можем думать об этом как о средней разнице между прогнозируемым значением содержания озона и фактическим наблюдаемым значением.
Мы также можем использовать следующий код для создания графика теста MSE на основе количества используемых деревьев:
#plot the MSE test by number of trees
plot(model)
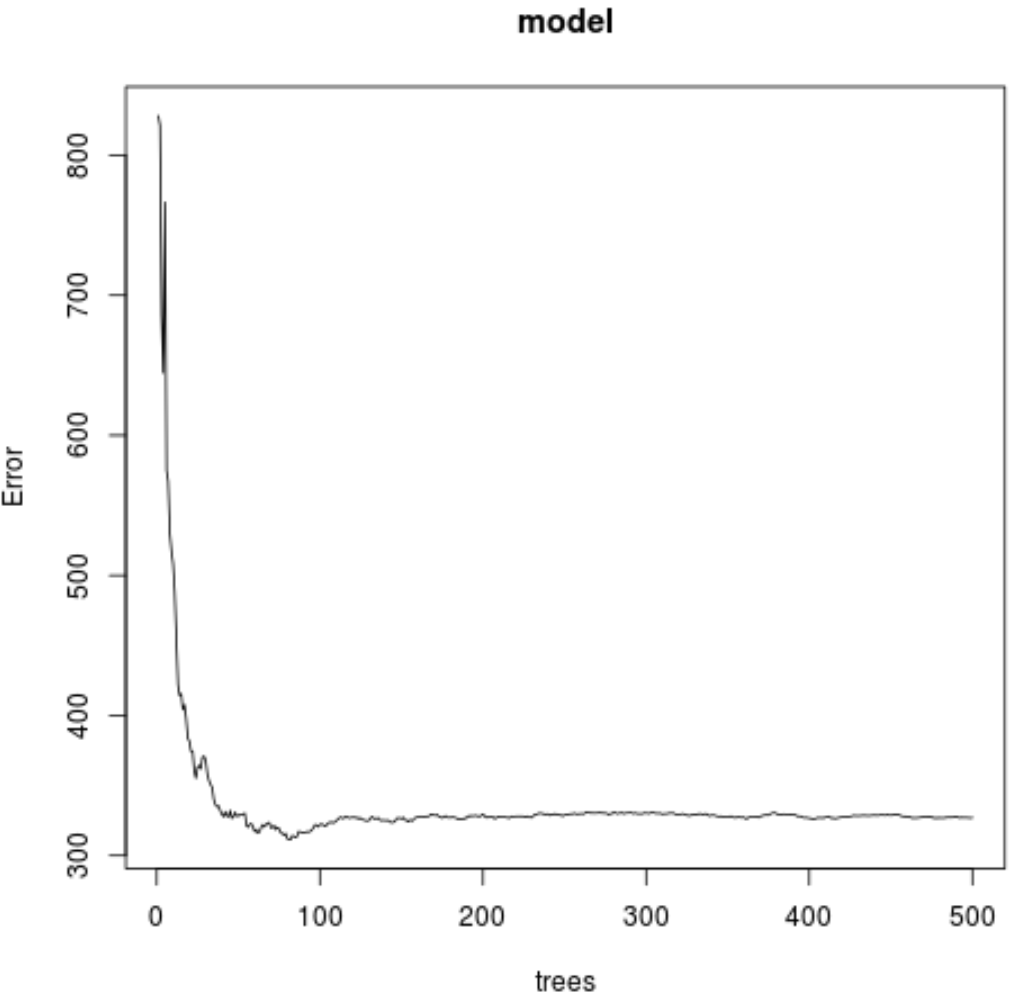
И мы можем использовать функцию varImpPlot() для создания графика, отображающего важность каждой переменной-предиктора в окончательной модели:
#produce variable importance plot
varImpPlot(model)
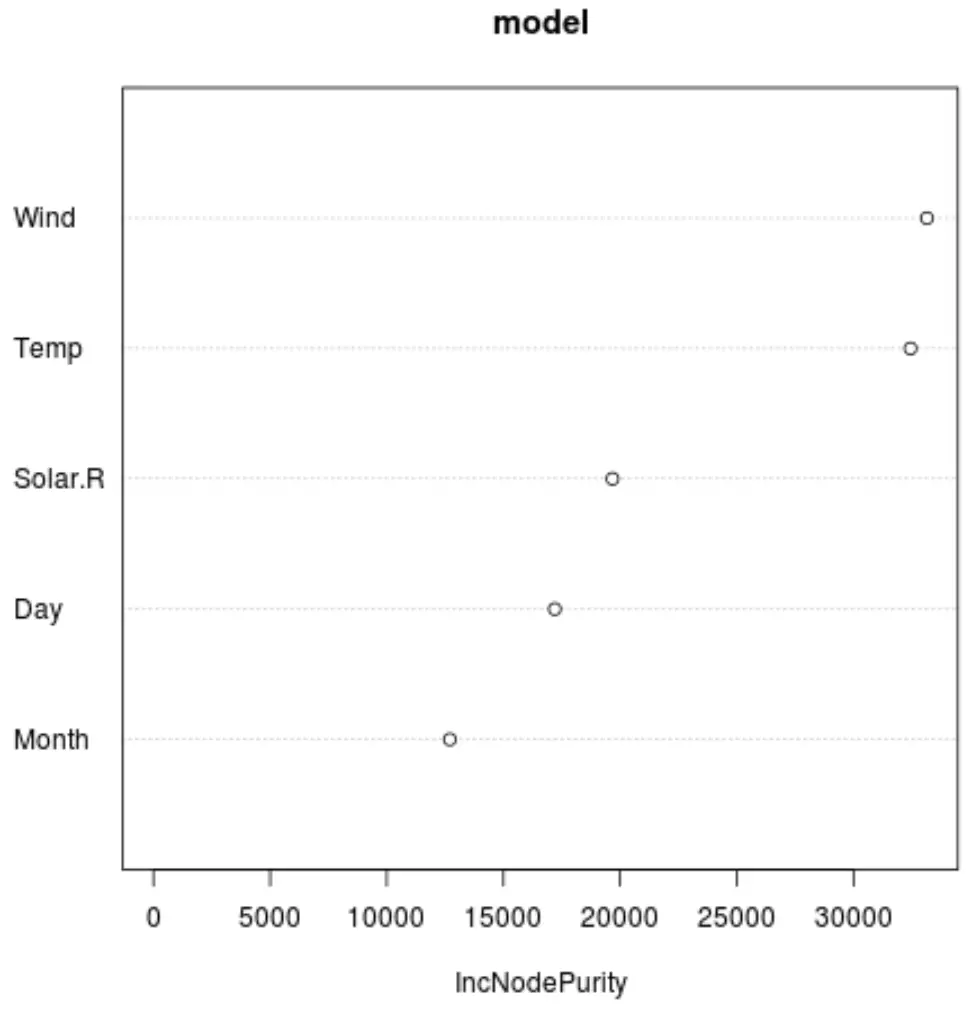
На оси X отображается среднее увеличение чистоты узлов деревьев регрессии как функция разделения по различным предикторам, отображаемым на оси Y.
На графике мы видим, что Wind является наиболее важной переменной-предиктором, за которой следует Temp .
Шаг 3: Настройте модель
По умолчанию функция randomForest() использует 500 деревьев и (всего предикторов/3) случайно выбранных предикторов в качестве потенциальных кандидатов для каждого разделения. Мы можем настроить эти параметры с помощью функции TuningRF() .
Следующий код показывает, как найти оптимальную модель, используя следующие спецификации:
- ntreeTry: количество деревьев, которые нужно построить.
- mtryStart: начальное количество переменных-предсказателей, которые следует учитывать при каждом делении.
- StepFactor: коэффициент, который будет увеличиваться до тех пор, пока расчетная ошибка выхода из сумки не перестанет улучшаться на определенную величину.
- улучшение: степень, на которую необходимо улучшить ошибку выхода мешка, чтобы продолжать увеличивать коэффициент шага.
model_tuned <- tuneRF(
x=airquality[,-1], #define predictor variables
y=airquality$Ozone, #define response variable
ntreeTry= 500 ,
mtryStart= 4 ,
stepFactor= 1.5 ,
improve= 0.01 ,
trace= FALSE #don't show real-time progress
)
Эта функция создает следующий график, который отображает количество предикторов, используемых при каждом разбиении при построении деревьев по оси X, и предполагаемую ошибку выхода из пакета по оси Y:
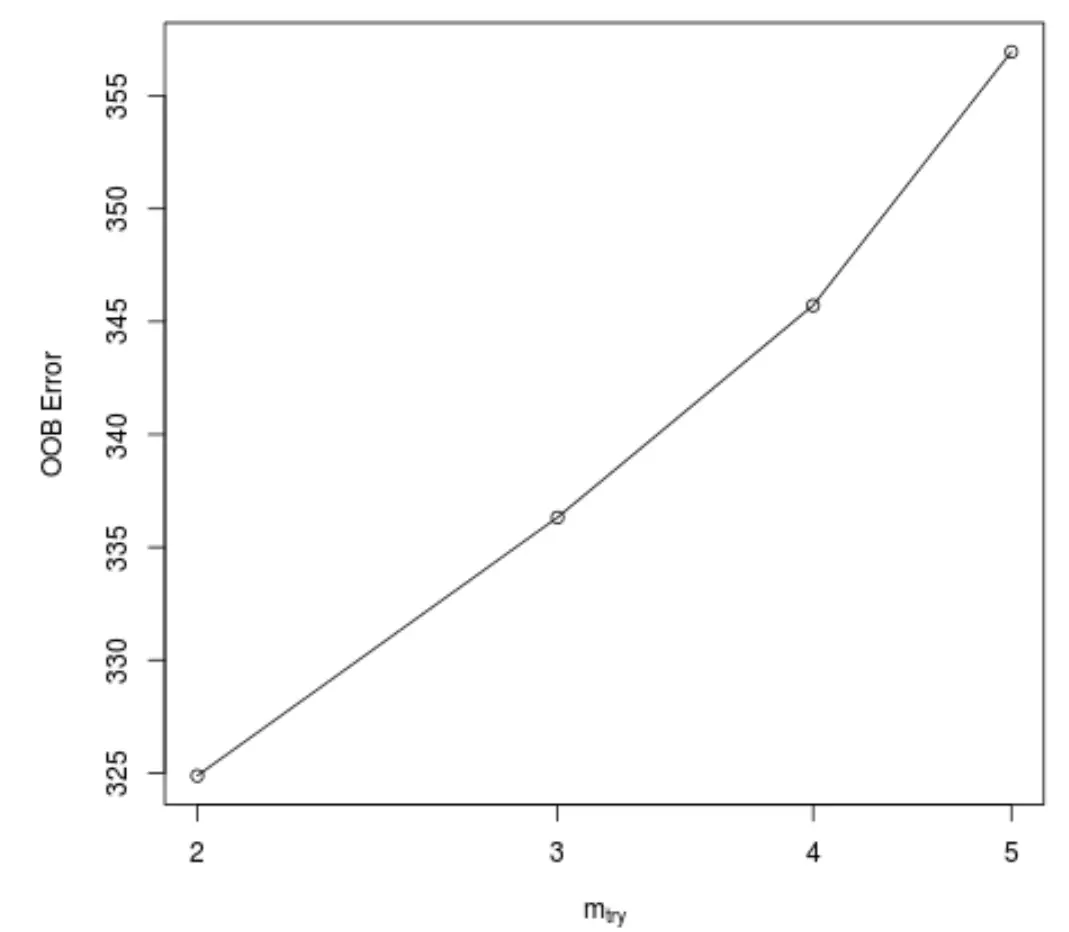
Мы видим, что наименьшая ошибка OOB получается при использовании двух случайно выбранных предикторов при каждом разбиении при построении деревьев.
Фактически это соответствует настройке по умолчанию (всего предикторов/3 = 6/3 = 2), используемой исходной функцией randomForest() .
Шаг 4. Используйте окончательную модель для прогнозирования
Наконец, мы можем использовать скорректированную модель случайного леса, чтобы делать прогнозы относительно новых наблюдений.
#define new observation new <- data.frame(Solar.R=150, Wind=8, Temp=70, Month=5, Day=5) #use fitted bagged model to predict Ozone value of new observation predict(model, newdata=new) 27.19442
На основе значений переменных-предикторов подобранная модель случайного леса предсказывает, что значение озона в этот конкретный день составит 27,19442 .
Полный R-код, использованный в этом примере, можно найти здесь .