Совокупная относительная частота

В этой статье объясняется, что такое совокупная относительная частота в статистике. Итак, вы найдете определение совокупной относительной частоты, способы получения совокупной относительной частоты и два упражнения, решаемые шаг за шагом.

Что такое совокупная относительная частота?

В статистике совокупная относительная частота представляет собой совокупную сумму относительных частот. То есть совокупная относительная частота значения равна относительной частоте этого значения плюс относительные частоты всех значений, меньших его.

Символ совокупной относительной частоты — H _i . Однако в статистике пока нет полного согласия относительно обозначения этого типа частоты, поэтому вы можете встретить его выражение и с помощью другого символа.

Очевидно, что чтобы понять значение совокупной относительной частоты, вы должны сначала иметь четкое представление о концепции относительной частоты, поэтому я рекомендую вам посетить следующую ссылку, прежде чем продолжить объяснение:

Как рассчитать совокупную относительную частоту

Для расчета совокупной относительной частоты необходимо выполнить следующие шаги:

1. Постройте таблицу частот со всеми различными значениями из статистической выборки.
2. Рассчитайте абсолютную частоту каждого значения.
3. По абсолютным частотам определите относительную частоту каждого значения.
4. Найдите совокупную относительную частоту каждого значения, которая рассчитывается путем сложения относительной частоты самого значения плюс относительные частоты всех меньших значений.

Имейте в виду, что если вы хотите рассчитать совокупную относительную частоту в процентах , то есть совокупную относительную частоту, выраженную в процентах, вам просто нужно выполнить те же действия и умножить результаты на 100.

Примеры совокупной относительной частоты

Чтобы вы могли увидеть, как рассчитывается совокупная относительная частота, ниже показаны два примера, решаемые шаг за шагом. В первом примере мы находим совокупную относительную частоту дискретной переменной, а во втором примере — непрерывной переменной, поскольку процесс меняется незначительно.

Пример 1: дискретная переменная

• Оценки, полученные по предмету «Статистика» в классе из 30 учащихся, следующие. Какова совокупная относительная частота каждой ноты?

В данном случае переменная является дискретной, так как не может принимать десятичное значение. Поэтому нет необходимости группировать данные по интервалам, а расчеты можно проводить напрямую.

Итак, составляем таблицу частот и определяем абсолютную частоту каждого отдельного значения:

Далее вычисляем относительную частоту каждого значения (как это делается, можно посмотреть по ссылке в начале поста).

И как только мы рассчитали абсолютную частоту и относительную частоту набора данных, мы можем получить совокупную относительную частоту. Для этого мы должны сложить относительную частоту рассматриваемого значения плюс все предыдущие относительные частоты или, другими словами, предыдущую накопленную относительную частоту:

Короче говоря, таблица частот с абсолютной частотой, относительной частотой и совокупной относительной частотой выглядит следующим образом:

Имейте в виду, что последнее значение совокупной относительной частоты всегда должно быть равно 1. Если вы получили другое число, значит, вы допустили ошибку в расчетах.

Пример 2: непрерывная переменная

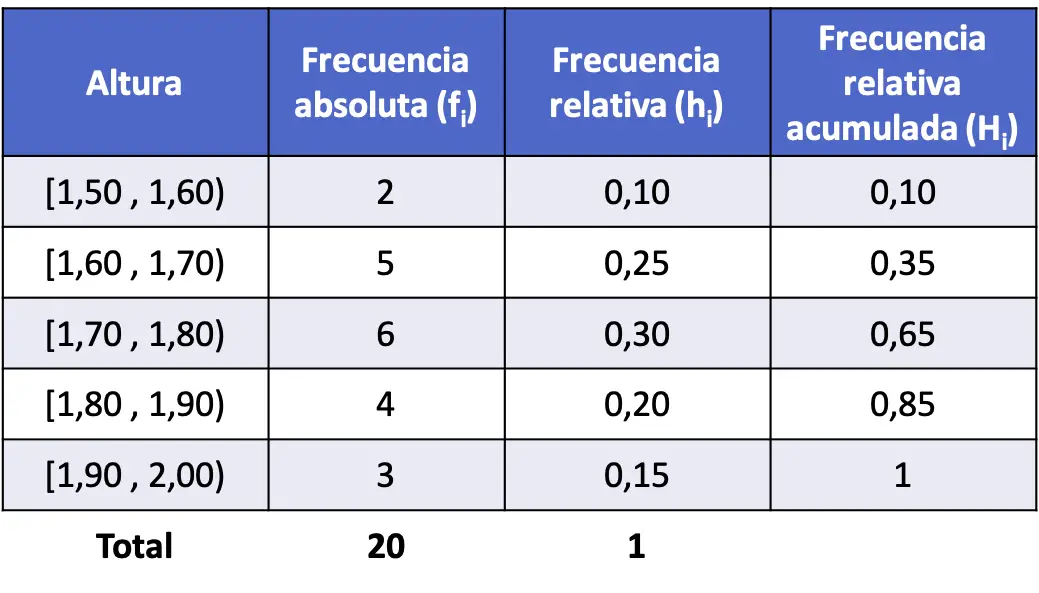
• Был измерен рост 20 человек и получены результаты, указанные ниже. Разделите данные на интервалы и найдите совокупную относительную частоту каждого интервала.

Этот случай отличается от предыдущей задачи тем, что числа десятичные, а это означает, что переменная может принимать любое значение и, следовательно, является непрерывной. Поэтому мы создадим таблицу частот, сгруппировав данные по интервалам.

Поэтому мы строим таблицу и получаем абсолютную частоту каждого интервала:

Теперь мы вычисляем относительные частоты, разделив абсолютную частоту каждого интервала на общее количество точек данных:

И, наконец, находим совокупные относительные частоты всех интервалов. Как и раньше, чтобы определить совокупную относительную частоту интервала, необходимо сложить относительную частоту указанного интервала плюс предыдущие относительные частоты:

Совокупная относительная частота и совокупная абсолютная частота

Мы только что увидели, как совокупная относительная частота получается из относительной частоты. Однако этот тип частоты также можно найти, используя накопленную абсолютную частоту.

Совокупную относительную частоту можно рассчитать путем деления совокупной абсолютной частоты на общее количество данных в выборке.

Следовательно, формула совокупной относительной частоты выглядит следующим образом:

Золото:

• 

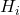
  — совокупная относительная частота.

• 

  — накопленная абсолютная частота .

• 

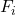
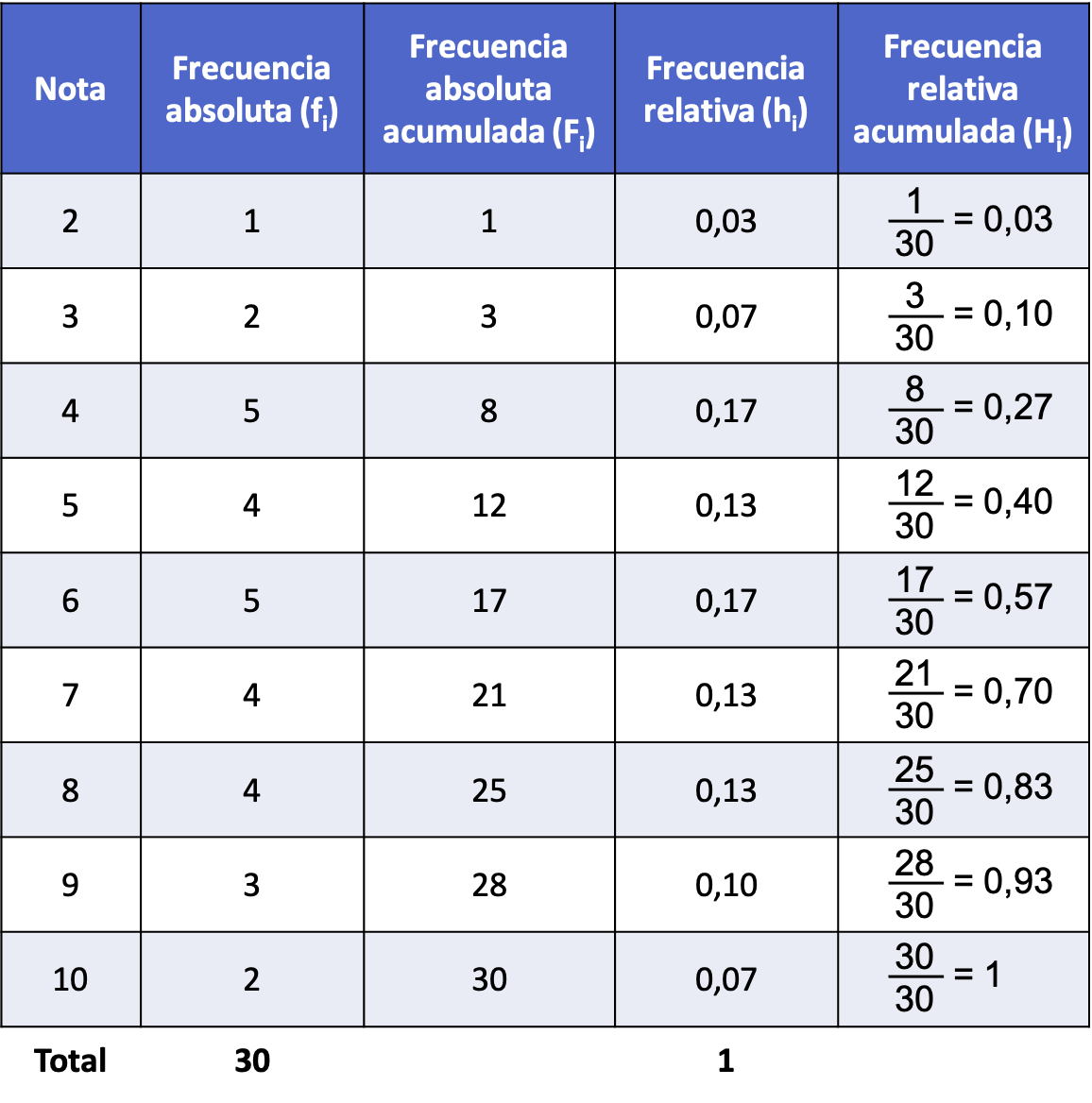
  общее количество данных.

Следуя первому примеру, разработанному выше, вот как накопленная относительная частота находится из накопленной абсолютной частоты:

Приведенная выше таблица, поскольку она содержит все виды статистических частот, называется таблицей частот. Нажмите здесь, чтобы узнать больше: