Как выполнить сплайн-регрессию в r (с примером)
Сплайновая регрессия — это тип регрессии, используемый, когда есть точки или «узлы», где структура данных резко меняется, а линейная регрессия и полиномиальная регрессия недостаточно гибки, чтобы соответствовать данным.
В следующем пошаговом примере показано, как выполнить сплайн-регрессию в R.
Шаг 1. Создайте данные
Во-первых, давайте создадим набор данных в R с двумя переменными и создадим диаграмму рассеяния, чтобы визуализировать связь между переменными:
#create data frame df <- data. frame (x=1:20, y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10, 11, 14, 15, 15, 16, 15, 17, 19, 18, 20)) #view head of data frame head(df) xy 1 1 2 2 2 4 3 3 7 4 4 9 5 5 13 6 6 15 #create scatterplot plot(df$x, df$y, cex= 1.5 , pch= 19 )
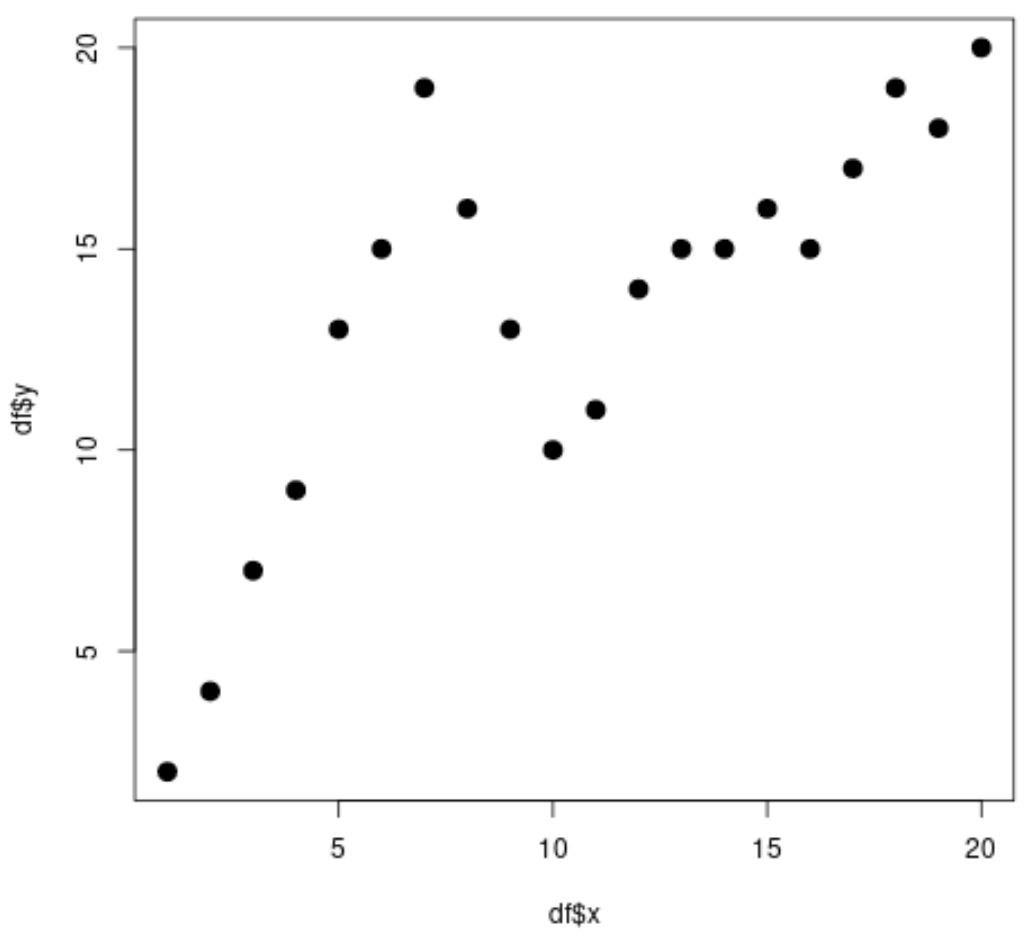
Очевидно, что связь между x и y нелинейна, и существуют две точки или «узла», где структура данных резко меняется при x=7 и x=10.
Шаг 2. Подберите простую модель линейной регрессии.
Затем давайте воспользуемся функцией lm() , чтобы подогнать простую модель линейной регрессии к этому набору данных и построить график, соответствующий линии регрессии на диаграмме рассеяния:
#fit simple linear regression model linear_fit <- lm(df$y ~ df$x) #view model summary summary(linear_fit) Call: lm(formula = df$y ~ df$x) Residuals: Min 1Q Median 3Q Max -5.2143 -1.6327 -0.3534 0.6117 7.8789 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 6.5632 1.4643 4.482 0.000288 *** df$x 0.6511 0.1222 5.327 4.6e-05 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.152 on 18 degrees of freedom Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05 #create scatterplot plot(df$x, df$y, cex= 1.5 , pch= 19 ) #add regression line to scatterplot abline(linear_fit)
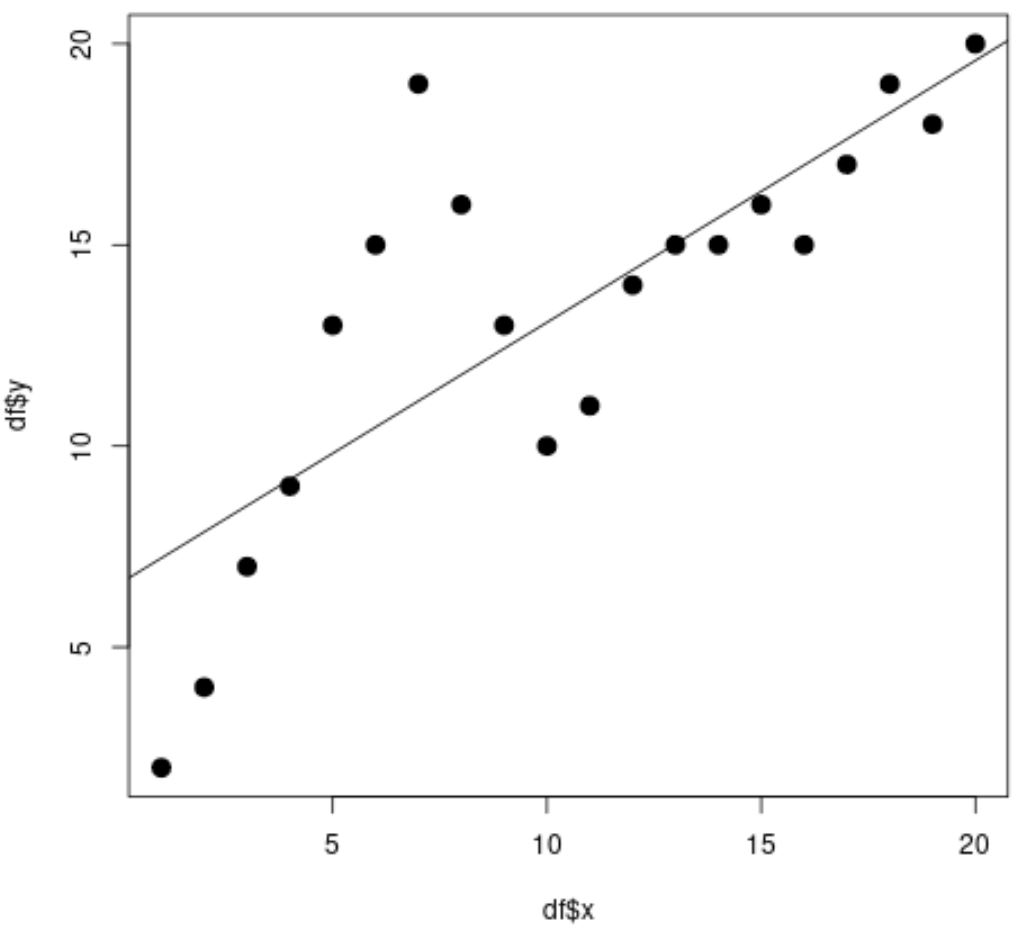
Из диаграммы рассеяния мы видим, что простая линия линейной регрессии плохо соответствует данным.
Из результатов модели мы также видим, что скорректированное значение R-квадрата составляет 0,5903 .
Мы сравним это со скорректированным значением R-квадрата сплайновой модели.
Шаг 3. Подберите модель сплайн-регрессии.
Далее давайте воспользуемся функцией bs() из пакета splines , чтобы подогнать модель сплайновой регрессии с двумя узлами, а затем построим подобранную модель на диаграмме рассеяния:
library (splines) #fit spline regression model spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 ))) #view summary of spline regression model summary(spline_fit) Call: lm(formula = df$y ~ bs(df$x, knots = c(7, 10))) Residuals: Min 1Q Median 3Q Max -2.84883 -0.94928 0.08675 0.78069 2.61073 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.073 1.451 1.429 0.175 bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514 bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 *** bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274 bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 *** bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 1.568 on 14 degrees of freedom Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07 #calculate predictions using spline regression model x_lim <- range(df$x) x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ]) preds <- predict(spline_fit, newdata=list(x=x_grid)) #create scatter plot with spline regression predictions plot(df$x, df$y, cex= 1.5 , pch= 19 ) lines(x_grid, preds)
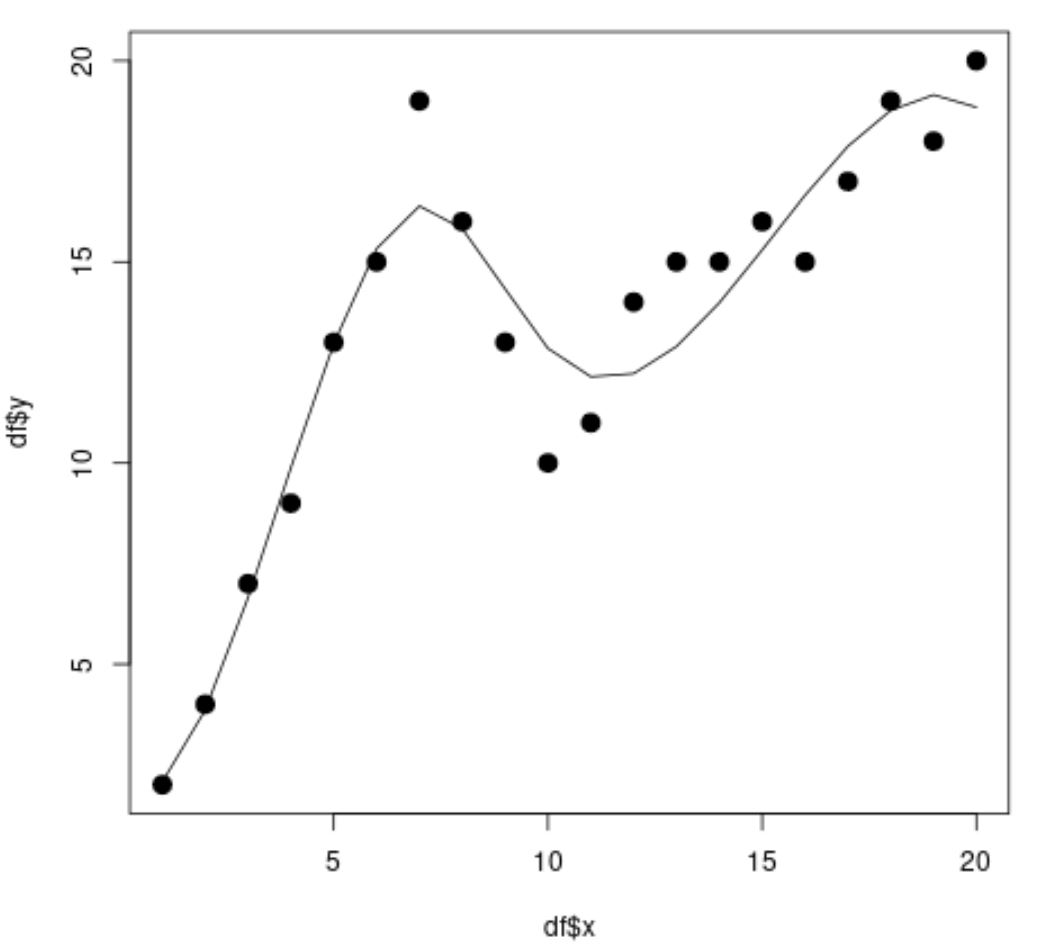
Из диаграммы рассеяния мы видим, что модель сплайновой регрессии вполне хорошо соответствует данным.
Из результатов модели мы также видим, что скорректированное значение R-квадрата составляет 0,8987 .
Скорректированное значение R-квадрата для этой модели намного выше, чем у простой модели линейной регрессии, что говорит нам о том, что модель сплайновой регрессии способна лучше соответствовать данным.
Обратите внимание, что для этого примера мы выбрали узлы, расположенные в точках x=7 и x=10.
На практике вам придется выбирать расположение узлов самостоятельно, исходя из того, где меняются закономерности в данных, и исходя из вашего опыта в предметной области.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в R:
Как выполнить множественную линейную регрессию в R
Как выполнить экспоненциальную регрессию в R
Как выполнить взвешенную регрессию наименьших квадратов в R