Как сравнивать гистограммы (с примерами)
Гистограмма — это тип диаграммы, позволяющий визуализировать распределение значений в наборе данных.
Ось X показывает значения набора данных, а ось Y показывает частоту каждого значения.
Гистограммы полезны, поскольку позволяют нам быстро понять распределение значений в наборе данных. Они также полезны для сравнения двух разных наборов данных.
Сравнивая две или более гистограмм, мы можем ответить на три разных вопроса:
1. Как сравниваются медианные значения?
Мы можем грубо оценить, что медиана находится около середины каждой гистограммы, что позволяет нам сравнивать медианные значения распределений.
2. Как соотносится дисперсия?
Мы можем визуально увидеть, какая гистограмма более разбросана, что дает нам представление о том, какое распределение имеет более разбросанные значения.
3. Чем отличается асимметрия?
Если гистограмма имеет «хвост» в левой части графика, говорят, что она имеет отрицательный перекос. И наоборот, если гистограмма имеет «хвост» на правой стороне графика, говорят, что она имеет положительный перекос. Мы можем визуально проверить каждую гистограмму, чтобы сравнить асимметрию .
В следующем примере показано, как сравнить две разные гистограммы и ответить на эти три вопроса.
Пример: сравнение гистограмм
Предположим, что 200 студентов используют один метод обучения для подготовки к экзамену, а еще 200 студентов используют другой метод обучения для подготовки к тому же экзамену.
Предположим, мы создаем следующие гистограммы для сравнения результатов экзаменов каждой группы студентов:
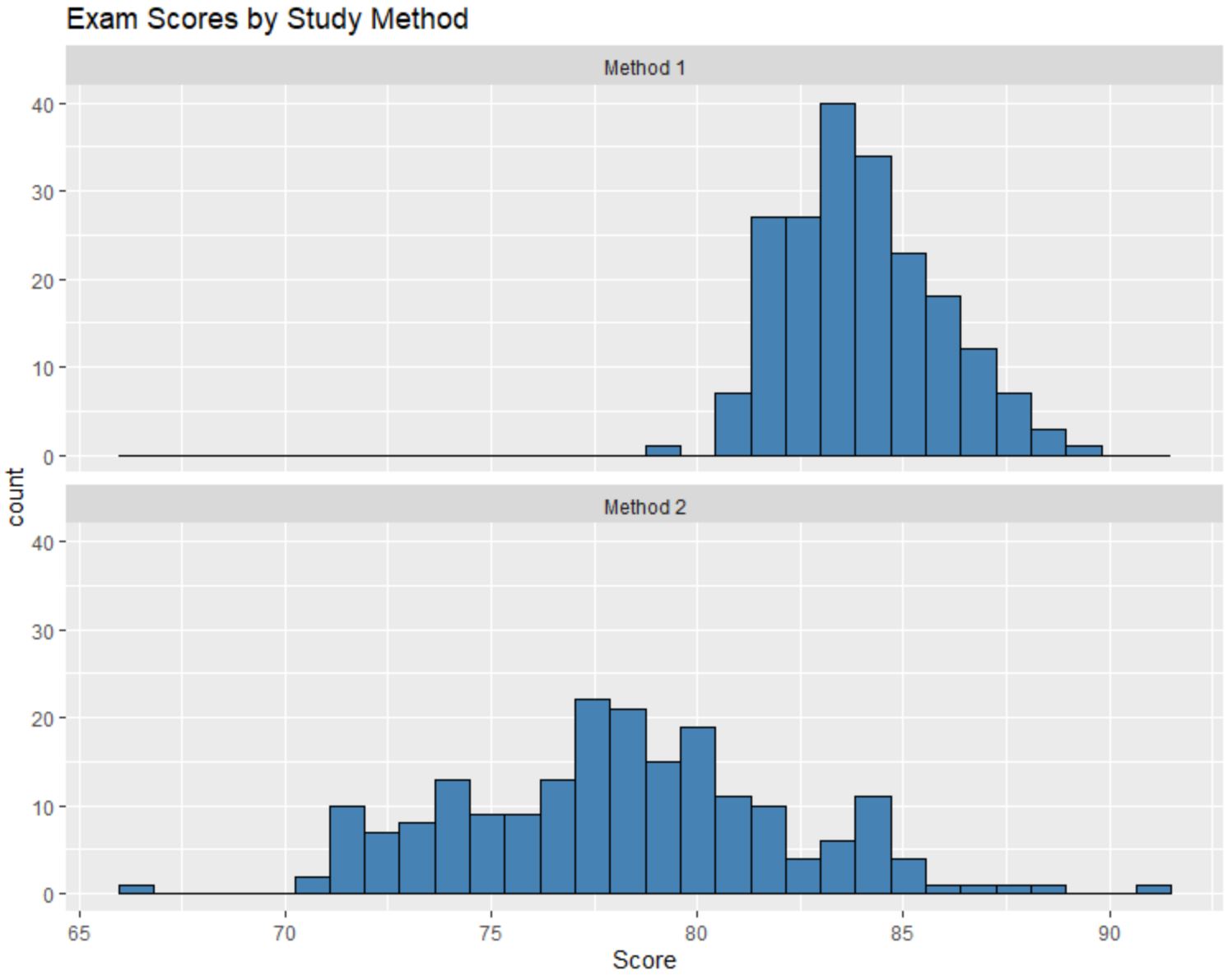
Мы можем сравнить эти гистограммы и ответить на следующие три вопроса:
1. Как сравниваются медианные значения?
Хотя мы не знаем точные медианные значения каждого распределения, просто глядя на гистограммы, очевидно, что средний балл на экзамене студентов, использовавших метод 1, выше, чем средний балл на экзамене студентов, использовавших метод 1. метод 2.
Мы могли бы оценить, что медианное значение для метода 1 составляет около 84, а медианное значение для метода 2 — около 78.
2. Как соотносится дисперсия?
Значения гистограммы для Метода 2 разбросаны гораздо сильнее, чем для Метода 1, что говорит нам о том, что разброс результатов экзамена у студентов, использовавших Метод 2, гораздо больше.
3. Чем отличается асимметрия?
Глядя на гистограммы, становится ясно, что распределение результатов тестов по методу 1 слегка смещено вправо, на что указывает «хвост», идущий справа от гистограммы.
Однако в распределении результатов экзамена по методу 2 не наблюдается «хвоста», что говорит нам о том, что распределение незначительно или не искажено.
Бонус : вот код, который мы использовали в R для создания этих двух гистограмм:
library (ggplot2)
#make this example reproducible
set. seeds (0)
#create data frame
df <- data. frame (method=rep(c(' Method 1 ', ' Method 2 '), each= 200 ),
Score=c(rnorm( 200 , mean= 84 , sd= 2 ),
rnorm( 200 , mean= 78 , sd= 4 )))
#create histogram of scores for each method
ggplot(df, aes(x=Score)) +
geom_histogram(fill=' steelblue ', color=' black ') +
facet_wrap(.~method, nrow= 2 ) +
labs(title=' Exam Scores by Study Method ')
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи с гистограммами:
Как оценить среднее и медиану любой гистограммы
Как оценить стандартное отклонение любой гистограммы
Как описать форму гистограмм