Как сравнивать коробчатые диаграммы: с примерами

Ящичковая диаграмма — это тип графика, на котором отображается пятизначная сводка набора данных, которая включает в себя:

• Минимальное значение
• Первый квартиль (25-й процентиль)
• Медианное значение
• Третий квартиль (75-й процентиль)
• Максимальное значение

Чтобы построить коробчатую диаграмму, мы рисуем прямоугольник от первого до третьего квартиля. Далее проводим вертикальную линию посередине. Наконец, рисуем «усы» квартилей до минимального и максимального значения.

Боксплоты полезны, поскольку позволяют нам быстро понять распределение значений в наборе данных. Они также полезны для сравнения двух разных наборов данных.

Сравнивая два или более коробчатых графика, мы можем ответить на четыре разных вопроса:

1. Как сравниваются медианные значения? Мы можем сравнить вертикальную линию в каждом поле, чтобы определить, какой набор данных имеет более высокое медианное значение.

2. Как соотносится дисперсия? Мы можем сравнить длину каждого прямоугольника (который представляет собой расстояние между Q1 и Q3 – межквартильный диапазон), чтобы определить, какой набор данных больше.

3. Чем отличается асимметрия? Чем ближе вертикальная линия к первому кварталу, тем более положительная асимметрия набора данных. Чем ближе вертикальная линия к третьему кварталу, тем более искажен набор данных.

4. Имеются ли выбросы? На коробчатых диаграммах выбросы обычно представляются крошечными кружками, выходящими за пределы каждого уса. Наблюдение определяется как выброс, если оно соответствует одному из следующих критериев:

• Одно наблюдение меньше Q1 – 1,5*IQR
• Наблюдение превышает Q3 + 1,5*IQR.

В следующем примере показано, как сравнить два разных коробчатых графика и ответить на эти четыре вопроса.

Пример: сравнение коробчатых диаграмм

Следующие наборы данных отображают результаты студентов, которые использовали один из двух методов обучения для подготовки к экзамену:

Метод 1: 78, 78, 79, 80, 80, 82, 82, 83, 83, 86, 86, 86, 86, 87, 87, 87, 88, 88, 88, 91.

Метод 2: 66, 66, 66, 67, 68, 70, 72, 75, 75, 78, 82, 83, 86, 88, 89, 90, 93, 94, 95, 98.

Если мы создадим коробчатые диаграммы для каждого набора данных, они будут выглядеть так:

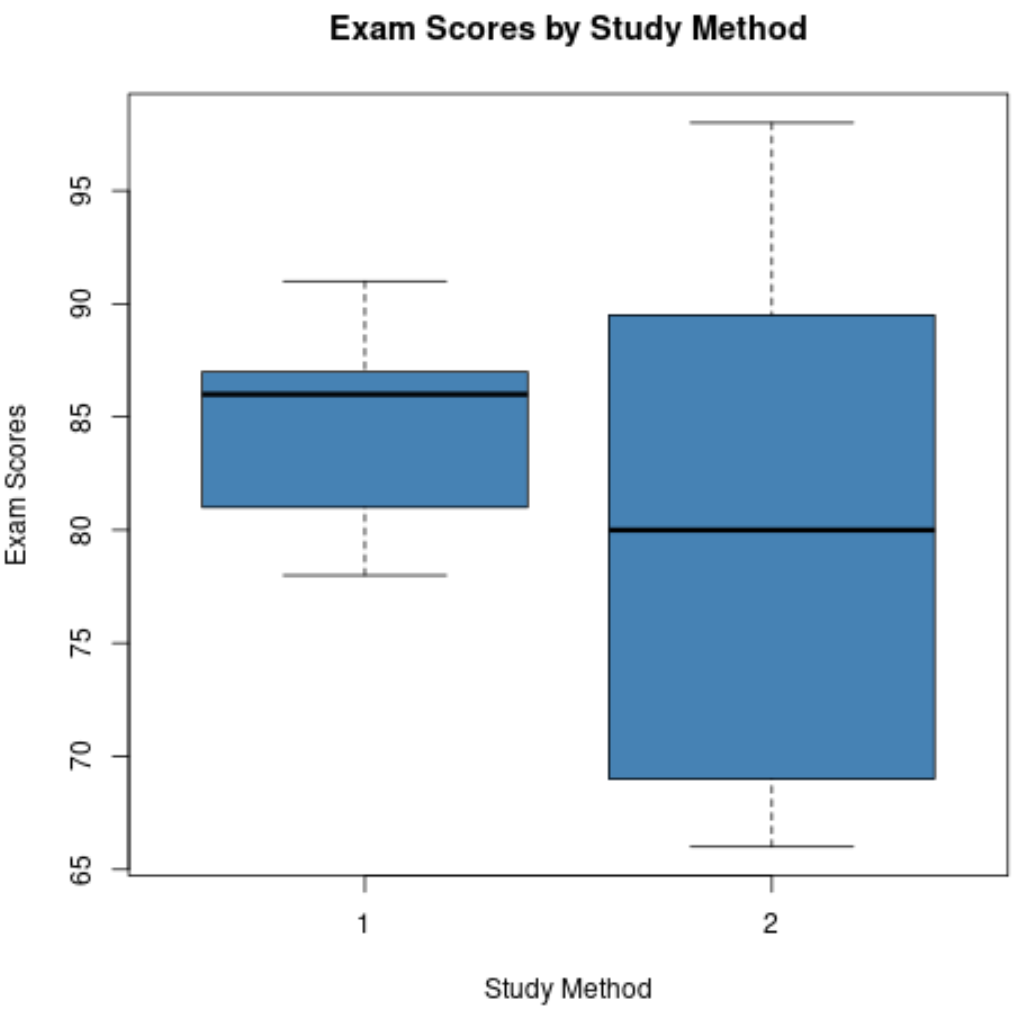
Мы можем сравнить эти два коробчатых графика и ответить на следующие четыре вопроса:

1. Как сравниваются медианные значения? Линия в середине диаграммы для метода обучения 1 выше линии для метода обучения 2, что указывает на то, что учащиеся, использовавшие метод обучения 1, получили среднюю оценку на высшем экзамене.

2. Как соотносится дисперсия? Ящичковая диаграмма для Метода обучения 2 намного длиннее, чем для Метода обучения 1, что указывает на то, что результаты экзаменов гораздо более распределены среди студентов, которые использовали Метод обучения 2.

3. Чем отличается асимметрия? Линия в середине квадратичной диаграммы для метода обучения 1 близка к Q3, что указывает на отрицательный перекос распределения экзаменационных баллов для студентов, использовавших метод обучения 1. И наоборот, линия в середине прямоугольника для метода исследования 2 расположена близко к центру прямоугольника, а это означает, что распределение баллов минимально искажено.

4. Имеются ли выбросы? Ни на одном коробчатом графике нет крошечных кружков, выходящих за верхние или нижние усы, а это означает, что ни один набор данных не имеет явных выбросов.

Дополнительные ресурсы

Как создавать и интерпретировать коробчатые диаграммы в Excel
Как создавать и интерпретировать коробчатые диаграммы в SPSS
Как создать несколько коробчатых диаграмм в R
Как создавать и интерпретировать коробчатые диаграммы в Stata