Средневзвешенное

К бенджамин андерсон 6 августа, 2023 Статистика 0 комментариев

Здесь мы объясним, что такое средневзвешенное значение и как оно рассчитывается. Вы сможете увидеть решенное упражнение о том, как найти средневзвешенное значение. Более того, вы можете вычислить средневзвешенное значение любого набора данных с помощью калькулятора в конце.

Что такое средневзвешенное значение?

Средневзвешенное значение является мерой центральности описательной статистики. Чтобы вычислить средневзвешенное значение, необходимо сначала умножить каждые статистические данные на их вес (или вес), затем сложить все продукты и, наконец, разделить взвешенную сумму на сумму всех весов.

Другими словами, формула средневзвешенного значения выглядит следующим образом:

Где x _i представляет каждую выборку данных, а w _i ее соответствующий вес.

Таким образом, чем больший вес имеет фрагмент данных, тем более важным он становится при расчете средневзвешенного значения. Другими словами, чем выше вес фрагмента данных, тем больше он повлияет на результат средневзвешенного значения.

Средневзвешенное значение особенно полезно для расчета оценок, поскольку оно позволяет с разной степенью важности оценивать упражнения или экзамены, сдаваемые во время курса. Средневзвешенное значение также используется для расчета ИПЦ (индекса потребительских цен), который является индикатором для измерения цен населения.

Помимо средневзвешенного, существуют и другие типы средних, такие как среднее геометрическое, среднее арифметическое, среднее квадратическое и среднее гармоническое.

Как рассчитать средневзвешенное значение

Для расчета средневзвешенного значения необходимо выполнить следующие шаги:

Умножьте каждые статистические данные на соответствующий вес.
Сложите все продукты, рассчитанные на предыдущем шаге.
Разделите взвешенную сумму, указанную выше, на сумму всех весов.
Полученный результат представляет собой средневзвешенное значение статистической выборки.

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать средневзвешенное значение любого набора данных.

Пример средневзвешенного значения

Что касается определения средневзвешенного значения, теперь мы решим упражнение, чтобы полностью понять, как средневзвешенное значение получается из набора данных.

Учащийся 1-го курса средней школы получил следующие оценки по предмету математика: 7 за частичный экзамен, что составляет 30%, 9 за групповую работу, что дает 20%, 6 за упражнения, данные на уроке с весом. 10% и 8 на выпускном экзамене, что имеет вес 40%. Какая у вас итоговая оценка по предмету?

Для определения оценки учащегося необходимо найти средневзвешенное значение, заданное в утверждении. Для этого применим формулу средневзвешенного значения:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

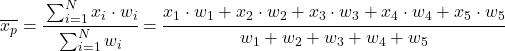
Оценка каждого результата представляет собой статистическое значение, а его процент соответствует весу указанного значения. Поэтому подставляем значения и веса в формулу и выполняем расчет средневзвешенного:

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

Таким образом, итоговая оценка этого ученика по математике будет 7,7, поскольку это результат, полученный на основе средневзвешенного значения.

Калькулятор средневзвешенного значения

Введите данные из любой статистической выборки и их соответствующие веса в калькулятор ниже, чтобы рассчитать средневзвешенное значение.

Введите статистические данные в первое поле и их соответствующие веса во второе поле. Вы должны записать веса в том же порядке, что и данные, и в десятичном формате. Все числа должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Стандартизированные веса

Как мы видели, в средневзвешенном значении вес — это значение, которое придается каждой части данных, чтобы придать ей большую или меньшую важность. Итак, если информация очень важна, она будет иметь очень высокий вес, но если информация не очень актуальна, она будет иметь очень низкий вес.

Итак, нормализованный вес — это тип взвешивания, используемый для получения средневзвешенного значения без какого-либо деления.

Нормализованный вес — это вес элемента данных, разделенный на сумму всех весов.

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

Таким образом, сумма всех нормализованных весов равна единице:

$\sum_{i=1}^N w_i'=1$

Итак, чтобы вычислить средневзвешенное значение с нормализованными весами , просто умножьте каждый элемент данных на его нормализованный вес:

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

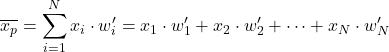
Например, у нас есть статистическая выборка, данные которой равны 24, 35, 17, 41, а их соответствующие веса равны 4, 9, 6, 3. Чтобы найти средневзвешенное значение этого набора данных, мы можем сначала вычислить нормализованные веса, разделив каждый вес по сумме всех весов:

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

А теперь просто умножьте каждые данные на их нормализованный вес, и результатом будет средневзвешенное значение:

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

Разница между средневзвешенным и средним арифметическим

Вычисление средневзвешенной и средней арифметической производится одинаково, так как операции должны быть выполнены схожие. При взвешенном усреднении каждая точка данных умножается на ее вес и делится на сумму весов, но при усреднении арифметики все данные складываются и делятся на общее количество точек данных.

Разница между средневзвешенным и средним арифметическим заключается в его понятии, поскольку в среднем арифметическом считается, что все данные имеют одинаковое значение, однако в средневзвешенном каждые данные имеют разный вес.

Обратите внимание: если все веса равны, средневзвешенное значение эквивалентно среднему арифметическому. Вы можете увидеть математическое доказательство ниже:

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше