Абсолютное среднее отклонение и стандартное отклонение: в чем разница?
Стандартное отклонение — один из наиболее распространенных способов измерения разброса набора данных.
Он рассчитывается следующим образом:
Стандартное отклонение = √( Σ(x i – x ) 2 / n)
Другой способ измерения распределения наблюдений в наборе данных — это среднее абсолютное отклонение .
Он рассчитывается следующим образом:
Среднее абсолютное отклонение = Σ|x i – x | /нет
В этом руководстве объясняются различия между этими двумя показателями, а также приводятся примеры расчета каждого из них.
Сходства и различия
Как следует из названия, стандартное отклонение и среднее абсолютное отклонение пытаются количественно оценить типичное отклонение наблюдений от среднего значения в данном наборе данных.
Однако метод , используемый для каждой метрики, различен.
Среднеквадратичное отклонение
Стандартное отклонение определяет квадрат разницы между каждым наблюдением и средним значением набора данных. Затем он усредняет эти квадраты разностей и извлекает квадратный корень.
В результате у нас остается число, которое представляет собой «стандартное» или типичное отклонение наблюдения от среднего значения.
Означает абсолютное отклонение
И наоборот, среднее абсолютное отклонение определяет абсолютное отклонение между каждым наблюдением и средним значением набора данных. Затем он находит среднее значение этих отклонений.
В результате у нас остается число, которое представляет собой среднее отклонение наблюдений от среднего значения.
Поскольку стандартное отклонение находит квадратичные различия, оно всегда будет равно или больше среднего абсолютного отклонения.
При наличии экстремальных выбросов стандартное отклонение будет значительно больше среднего абсолютного отклонения. Следующий пример иллюстрирует этот момент.
Пример: среднее абсолютное отклонение от стандартного отклонения.
Предположим, у нас есть следующий набор данных из 8 значений:
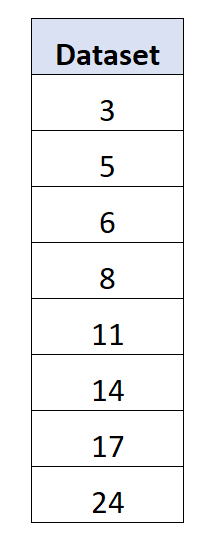
В среднем получается 11 .
Итак, мы рассчитаем среднее абсолютное отклонение следующим образом:
Среднее абсолютное отклонение = (|3-11| + |5-11| + |6-11| + |8-11| + |11-11| + |14-11| + |17-11| + |24- 11|)/8 = 5,5 .
И мы рассчитаем стандартное отклонение следующим образом:
Стандартное отклонение = √((3-11) 2 + (5-11) 2 + (6-11) 2 + (8-11) 2 + (11-11) 2 + (14-11) 2 + (17- 11) 2 + (24-11) 2 )/8) = 6,595 .
Как упоминалось ранее, стандартное отклонение всегда будет равно или больше среднего абсолютного отклонения.
Однако разница между стандартным отклонением и средним абсолютным отклонением будет особенно велика, если в наборе данных имеются экстремальные выбросы.
Например, рассмотрим следующий набор данных с экстремальным выбросом для последнего значения:
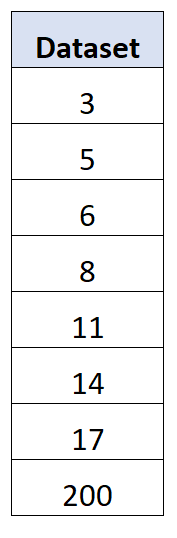
Оказывается, стандартное отклонение для этого набора данных составляет 63,27 , а среднее абсолютное отклонение — 41,75 .
Экстремальный выброс приводит к тому, что стандартное отклонение намного превышает среднее абсолютное отклонение.
Об авторе
бенджамин андерсон
Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше