Среднее арифметическое
Здесь мы объясним, что такое среднее арифметическое и как оно рассчитывается. Вы найдете примеры среднего арифметического значения и даже калькулятор, позволяющий найти среднее арифметическое любой статистической выборки. Наконец, вы сможете увидеть, каковы свойства этого типа среднего и как получается среднее арифметическое с данными, сгруппированными по интервалам.
Что такое среднее арифметическое?
Среднее арифметическое является центральной величиной, характеризующей набор статистических данных. Для расчета среднего арифметического все значения складываются и делятся на общее количество данных.
Кроме того, среднее арифметическое является одним из основных показателей, используемых при проведении статистического исследования выборки.
Таким образом, формула среднего арифметического выглядит следующим образом:
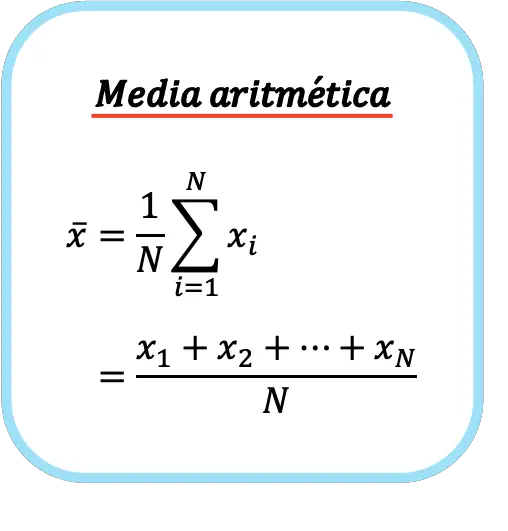
Символ среднего арифметического представляет собой горизонтальную полосу над буквой х.
![]()
Вы также можете отличить выборочное среднее от среднего с помощью символа среднего: среднее значение выборки выражается символом
![]()
, с другой стороны, для обозначения средней численности населения мы используем греческую букву
![]()
Следует отметить, что среднее арифметическое генеральной совокупности эквивалентно ожидаемому значению статистической переменной.
Среднее арифметическое, также называемое средним арифметическим, не является единственным существующим типом среднего. Среди прочих существуют также средневзвешенное, среднее квадратическое, среднее геометрическое и среднее гармоническое. Посмотреть, как рассчитывается каждый из них, можно в поисковике нашего сайта.
Как посчитать среднее арифметическое
Для расчета среднего арифметического необходимо выполнить следующие действия:
- Добавьте все статистические данные из выборки.
- Разделите предыдущую сумму на общее количество данных.
- Полученный результат представляет собой среднее арифметическое статистической выборки.
👉 Вы можете использовать калькулятор ниже, чтобы вычислить среднее арифметическое любого набора данных.
Пример расчета среднего арифметического
Учитывая определение среднего арифметического, мы увидим, как получить среднее арифметическое набора данных, шаг за шагом решая пример.
- За учебный год учащийся получил следующие оценки: по математике — 9, по языку — 7, по истории — 6, по экономике — 8 и по естественным наукам — 7,5. Каково среднее арифметическое всех ваших оценок?
Чтобы найти среднее арифметическое, нам нужно сложить все оценки, а затем разделить на общее количество предметов в курсе, которое равно 5. Поэтому применим формулу среднего арифметического:
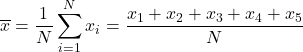
Подставляем данные в формулу и вычисляем среднее арифметическое:
![]()
Как видите, в среднем арифметическом каждому значению присваивается одинаковый вес, то есть каждый фрагмент данных имеет одинаковый вес в целом.
Калькулятор среднего арифметического значения
Введите данные из любой статистической выборки в следующий калькулятор, чтобы вычислить ее среднее арифметическое. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.
Среднее арифметическое для сгруппированных данных
Под сгруппированными данными мы подразумеваем, что данные структурированы в виде групп или интервалов. Обычно это происходит, когда размер статистической выборки очень велик.
Таким образом, вычисление среднего арифметического немного меняется, когда данные сгруппированы вместе, хотя концепция та же самая.
Чтобы вычислить среднее арифметическое данных, сгруппированных в интервалы, балл класса каждой группы необходимо умножить на ее абсолютную частоту, а затем разделить на сумму всех абсолютных частот.
![]()
Примечание. Оценка класса интервала рассчитывается путем деления суммы конечных точек интервала на два. Например, классная заметка интервала [3,7) будет такой:
![]()
Чтобы вы могли увидеть, как это делается, ниже приведено решенное упражнение на среднее арифметическое данных, сгруппированных по интервалам:
- Мы хотим статистически изучить вес группы, для этого мы опросили репрезентативную группу из 81 человека и получили следующие данные:
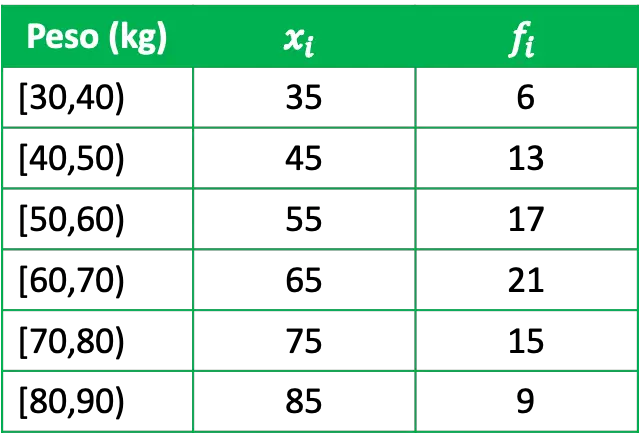
Где x i — классный балл каждой группы, а f i — ее абсолютная частота, то есть количество людей, имеющих вес в этом интервале.
Чтобы определить среднее арифметическое, необходимо добавить в таблицу частот столбец, который представляет собой произведение примечаний к классу на соответствующие абсолютные частоты:
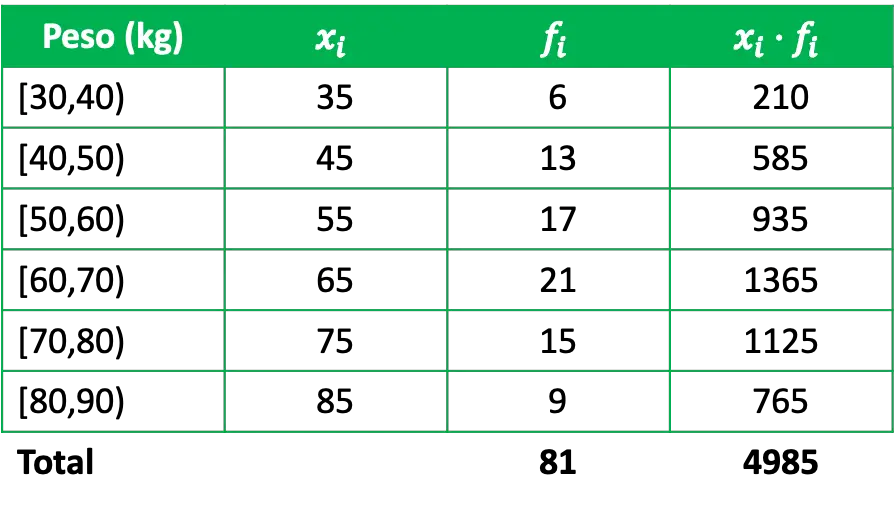
Таким образом, чтобы вычислить среднее арифметическое сгруппированных данных, просто разделите сумму произведений классных примечаний на их частоты на общее количество данных:
![]()
Свойства среднего арифметического
Среднее арифметическое имеет следующие характеристики:
- Сумма отклонений всех данных в распределении от среднего значения равна нулю.
![]()
- Если мы добавим одинаковую сумму ко всем данным в выборке, среднее значение выборки увеличится на эту сумму.
- То же самое происходит и с умножением: если все значения выборки умножить на число, среднее значение выборки умножится на это число.
- Среднее арифметическое можно вычислить только в количественных переменных . Другими словами, вы не можете взять среднее значение качественных переменных.
- Среднее арифметическое всегда будет значением между минимумом и максимумом распределения.
![]()
- Этот тип среднего значения очень чувствителен к очень высоким или очень низким значениям, в результате чего выброс существенно меняет результат среднего арифметического.
- Среднее арифметическое набора данных всегда равно или больше среднего геометрического того же набора данных.
![]()
Вычислить среднее арифметическое с помощью Excel
Вычислить среднее арифметическое в Excel очень просто, так как вам достаточно ввести данные на лист и воспользоваться функцией СРЗНАЧ .
Например, чтобы определить среднее арифметическое данных из первого решенного упражнения, которое мы объяснили, просто скопируйте все данные в документ Excel и напишите в ячейке следующую формулу: =СРЗНАЧ(9;7;5; 8;7 ,5) . Функция вернет среднее арифметическое значение данных, равное 7,3.
Очевидно, что найти среднее арифметическое некоторых чисел с помощью программы Excel гораздо быстрее, чем вычислять его вручную, особенно когда размер выборки очень велик.