Как рассчитать среднеквадратическую ошибку (rmse) в excel
В статистике регрессионный анализ — это метод, который мы используем, чтобы понять взаимосвязь между переменной-предиктором x и переменной отклика y.
Когда мы выполняем регрессионный анализ, мы получаем модель, которая сообщает нам прогнозируемое значение переменной ответа на основе значения переменной-предиктора.
Один из способов оценить, насколько хорошо наша модель соответствует заданному набору данных, — это вычислить среднеквадратическую ошибку , которая является показателем, который говорит нам, насколько в среднем далеки наши прогнозируемые значения от наблюдаемых значений.
Формула для нахождения среднеквадратической ошибки, более известная как RMSE , выглядит следующим образом:
RMSE знак равно √[ Σ(P i – O i ) 2 / n ]
Золото:
- Σ — причудливый символ, означающий «сумма».
- Pi — прогнозируемое значение для i-го наблюдения в наборе данных.
- O i — наблюдаемое значение для i-го наблюдения в наборе данных.
- n — размер выборки
Технические примечания :
- Среднеквадратическую ошибку можно рассчитать для любого типа модели, дающей прогнозируемые значения, которые затем можно сравнить с наблюдаемыми значениями набора данных.
- Среднеквадратическую ошибку также иногда называют среднеквадратичным отклонением, которое часто называют RMSD.
Далее давайте рассмотрим пример того, как рассчитать среднеквадратическую ошибку в Excel.
Как рассчитать среднеквадратическую ошибку в Excel
В Excel нет встроенной функции для расчета RMSE, но мы можем легко вычислить ее с помощью одной формулы. Мы покажем, как рассчитать RMSE для двух разных сценариев.
Сценарий 1
В сценарии у вас может быть один столбец, содержащий прогнозируемые значения из вашей модели, и другой столбец, содержащий наблюдаемые значения. На изображении ниже показан пример этого сценария:
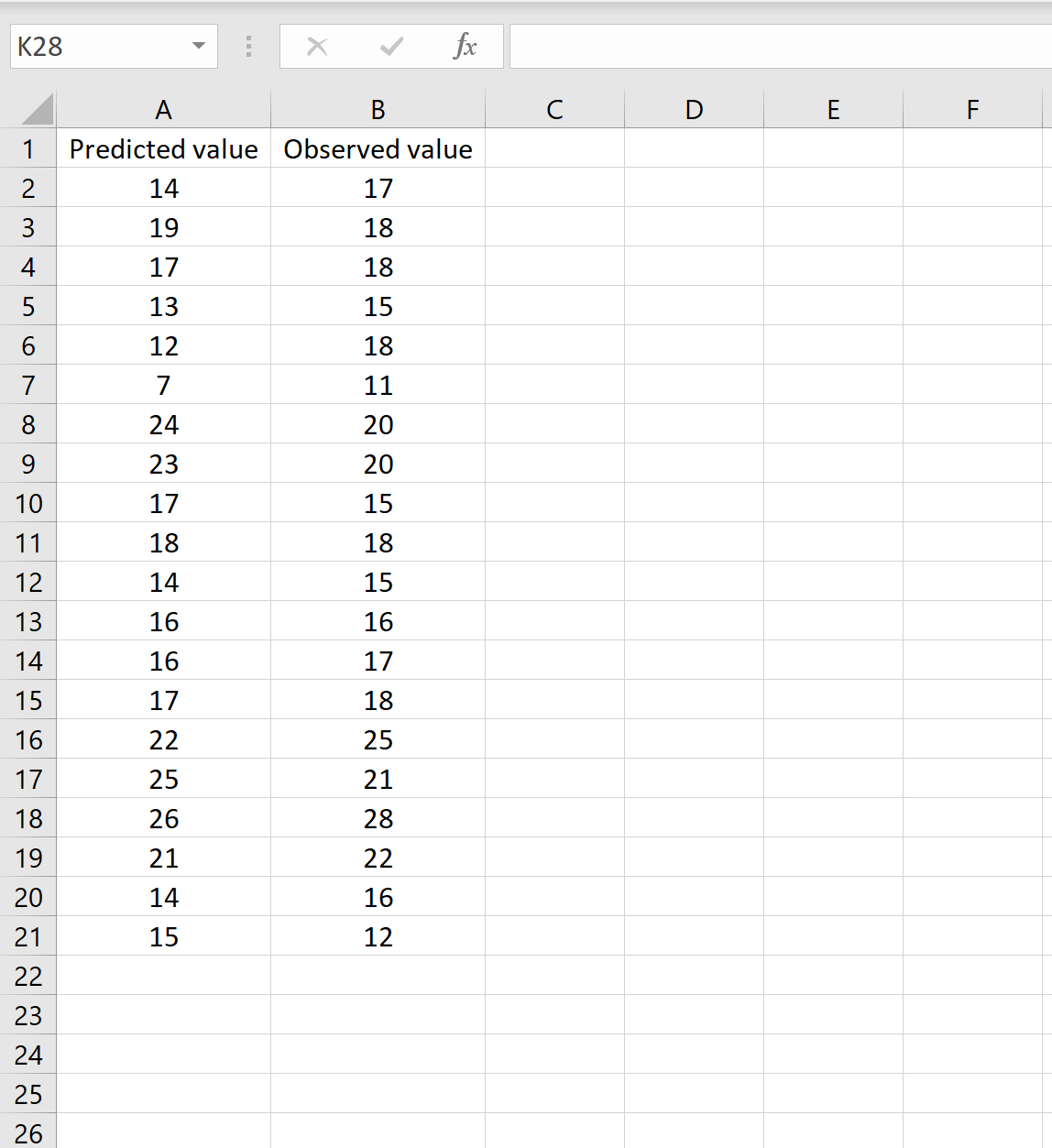
Если это так, вы можете вычислить RMSE, введя следующую формулу в любую ячейку и нажав CTRL+SHIFT+ВВОД:
=КОРЕНЬ(СУММQ(A2:A21-B2:B21) / СЧЁТ(A2:A21))
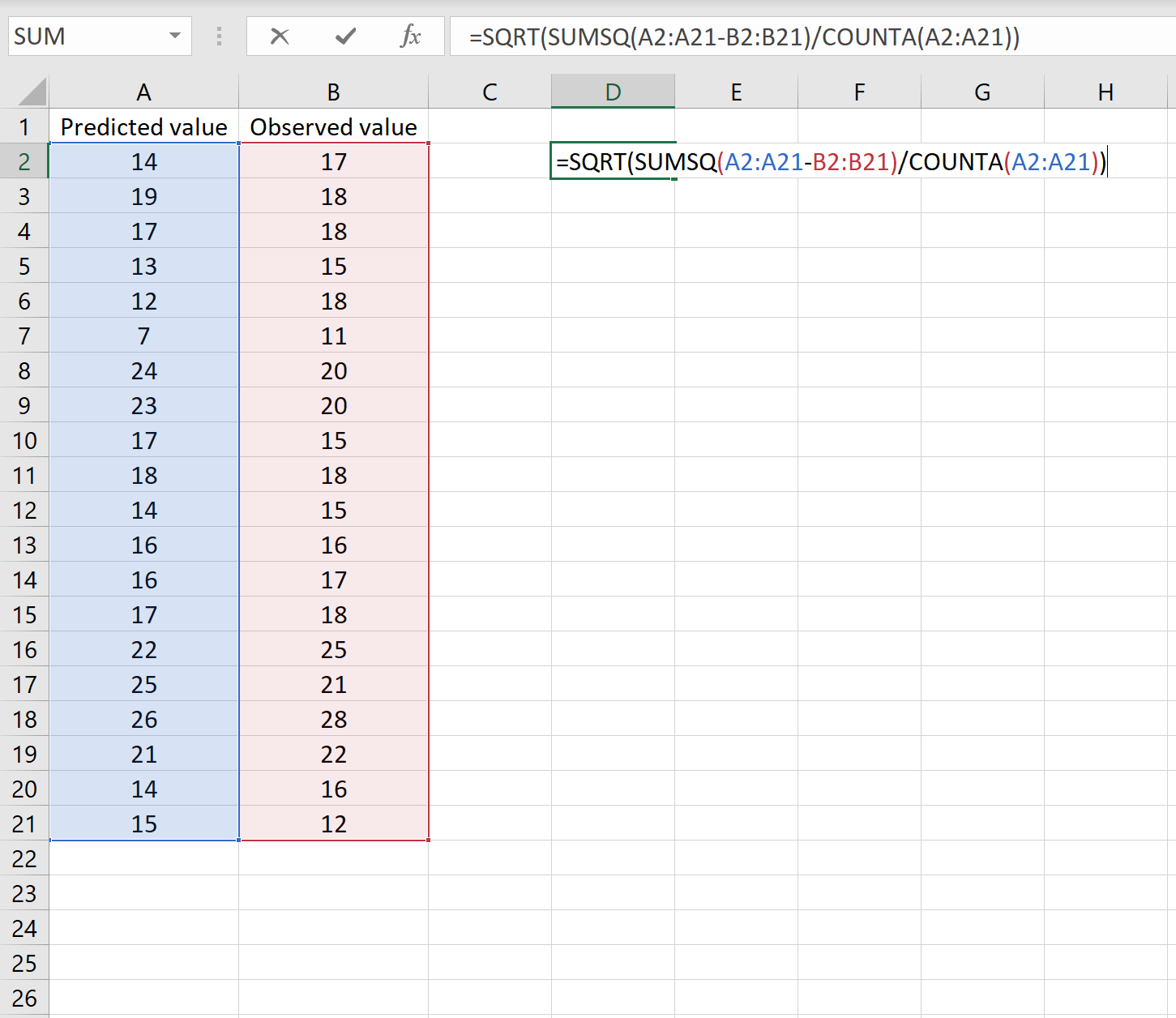
Это говорит нам о том, что среднеквадратическая ошибка равна 2,6646 .
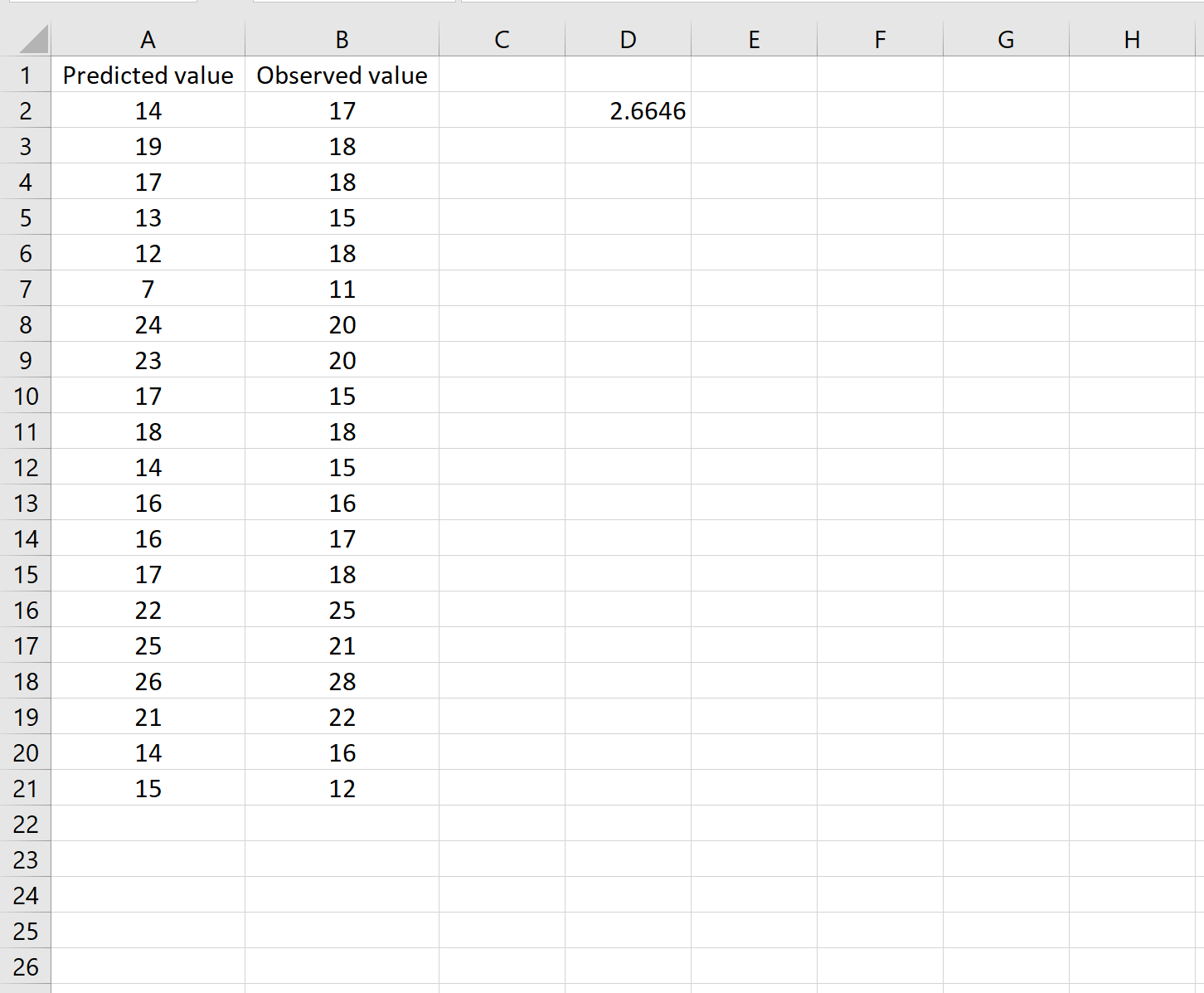
Формула может показаться немного сложной, но она обретет смысл, если разобраться:
= КОРЕНЬ( СУММQ(A2:A21-B2:B21) / СЧЁТ(A2:A21) )
- Сначала мы вычисляем сумму квадратов разностей между прогнозируемыми и наблюдаемыми значениями с помощью функции SUMSQ() .
- Затем мы делим набор данных на размер выборки с помощью COUNTA() , который подсчитывает количество непустых ячеек в диапазоне.
- Наконец, мы извлекаем квадратный корень из всего расчета с помощью функции КОРЕНЬ() .
Сценарий 2
В другом сценарии вы, возможно, уже рассчитали разницу между прогнозируемыми и наблюдаемыми значениями. В этом случае у вас будет только один столбец, показывающий различия.
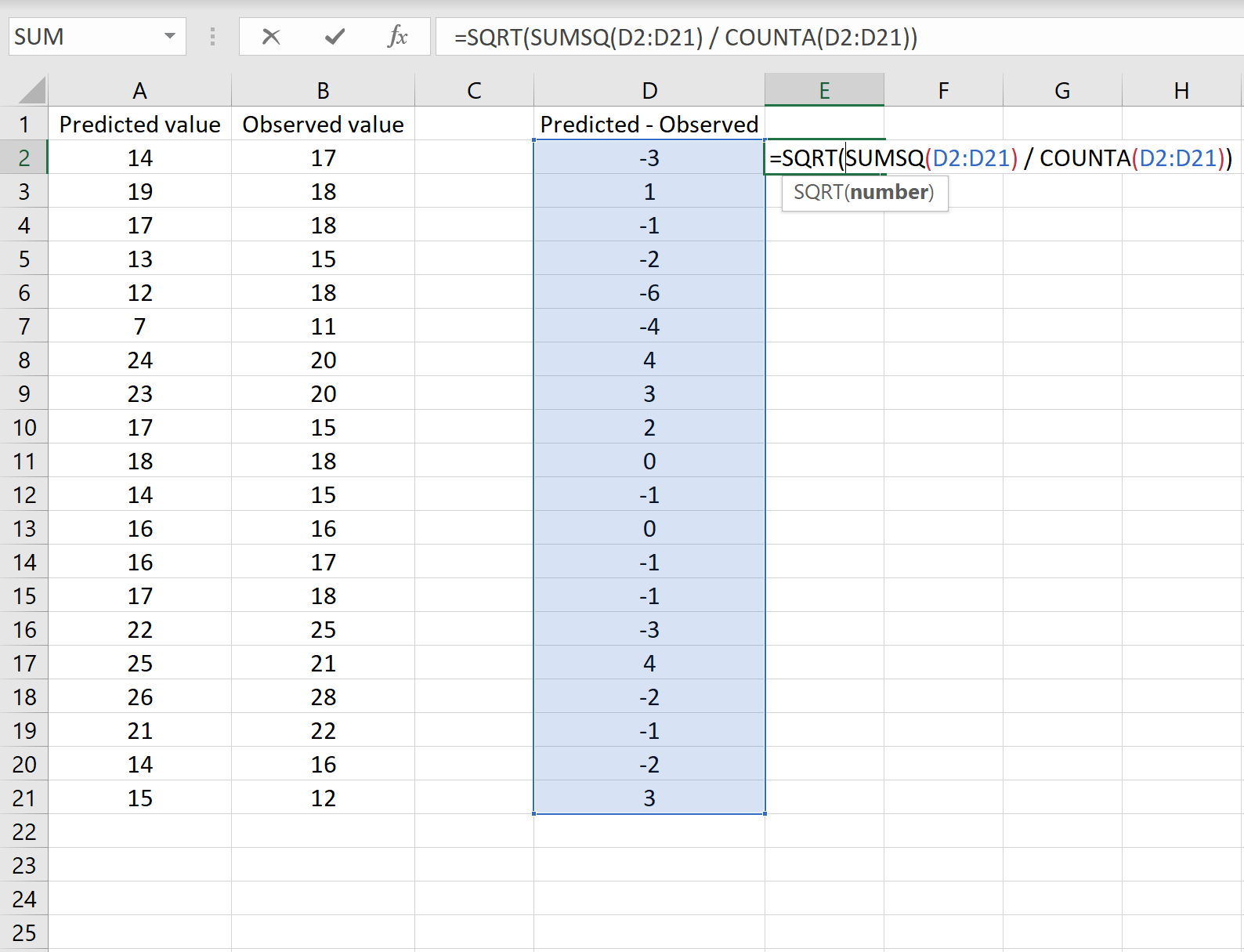
На изображении ниже показан пример этого сценария. Прогнозируемые значения показаны в столбце A, наблюдаемые значения — в столбце B, а разница между прогнозируемыми и наблюдаемыми значениями — в столбце D:
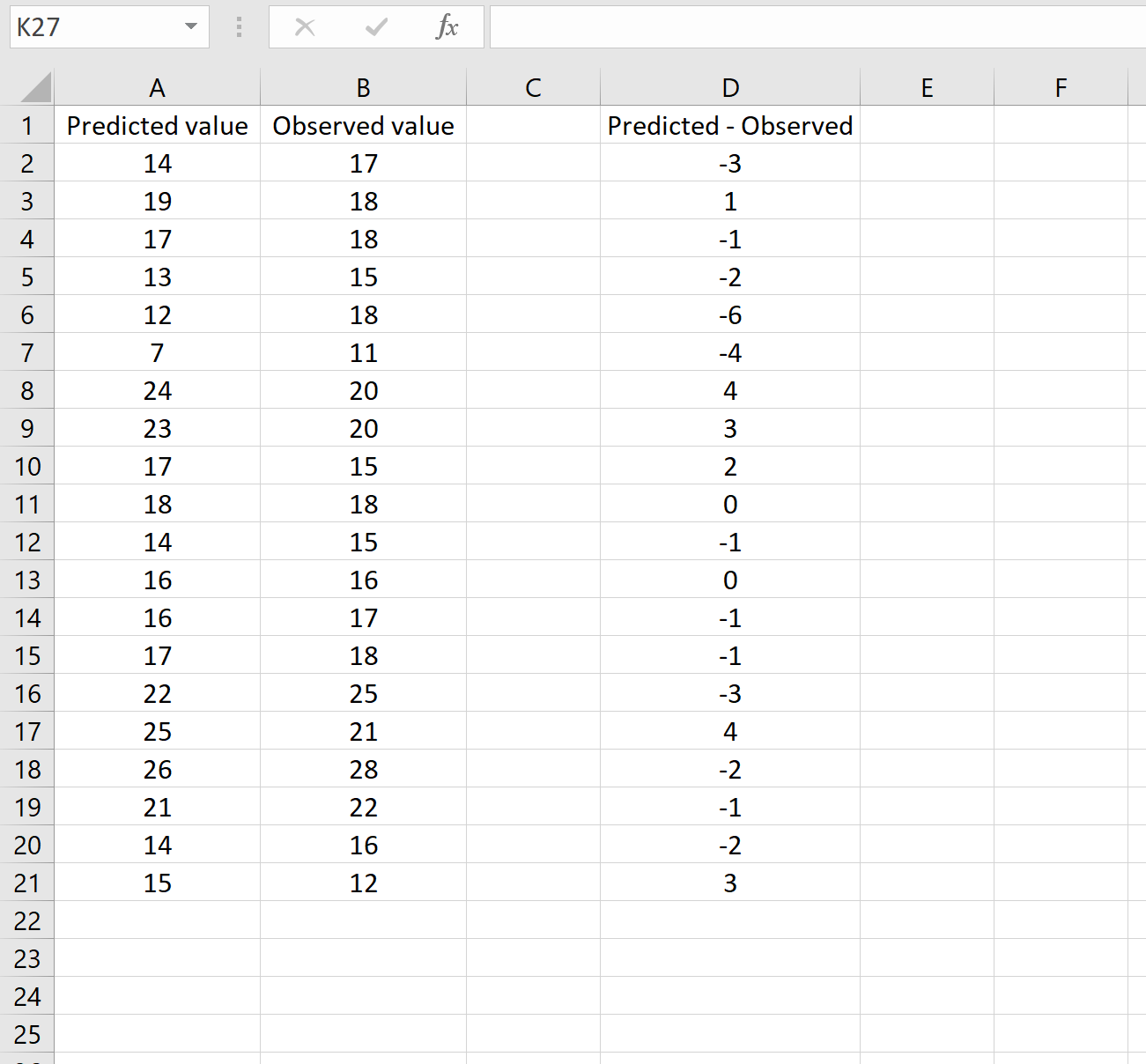
Если это так, вы можете вычислить RMSE, введя следующую формулу в любую ячейку и нажав CTRL+SHIFT+ВВОД:
=КОРЕНЬ(СУММQ(D2:D21) / СЧЁТ(D2:D21))
Это говорит нам о том, что среднеквадратическая ошибка равна 2,6646 , что соответствует результату, полученному в первом сценарии. Это подтверждает, что эти два подхода к расчету RMSE эквивалентны.
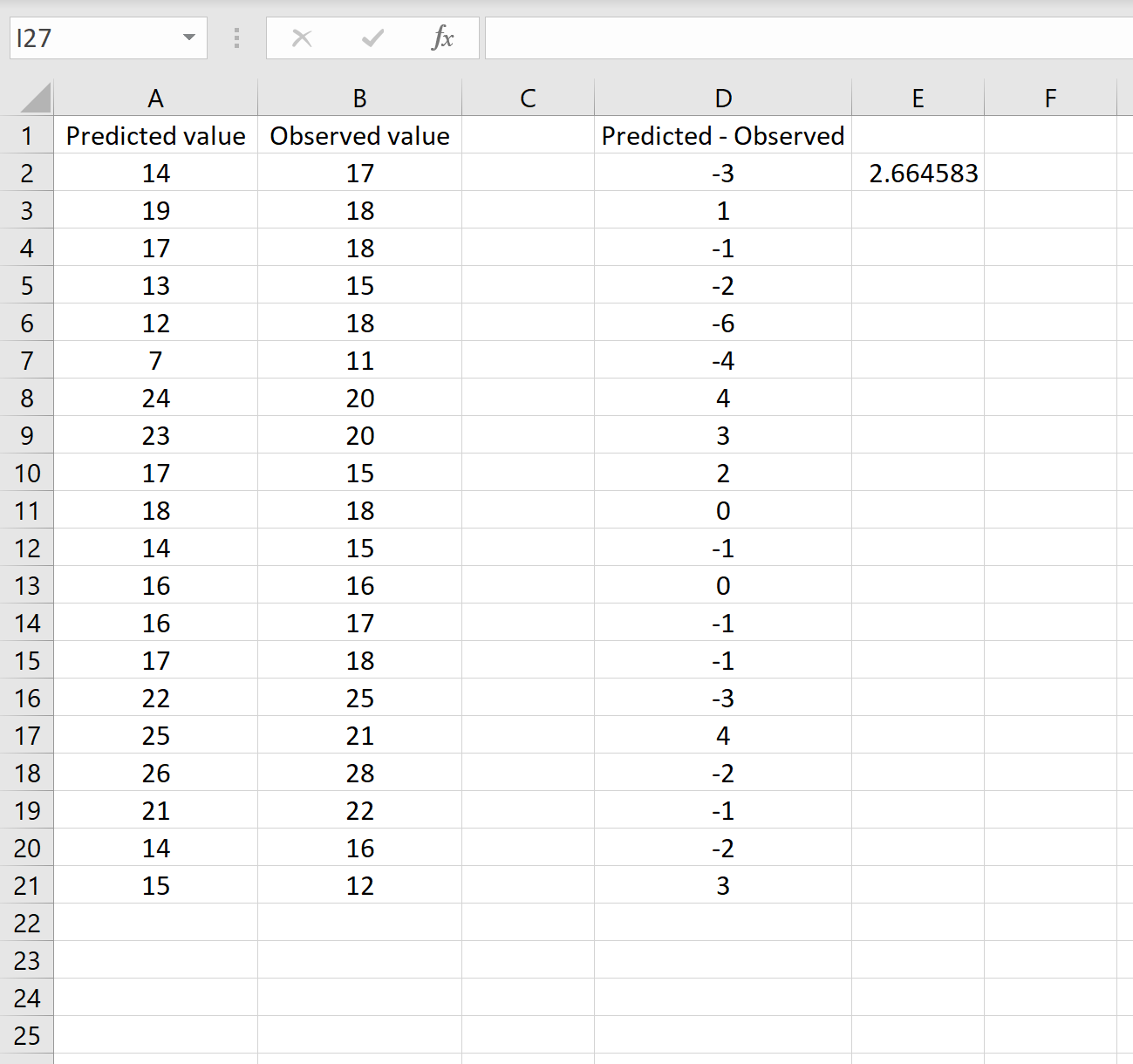
Формула, которую мы использовали в этом сценарии, лишь немного отличается от той, которую мы использовали в предыдущем сценарии:
= КОРЕНЬ( СУММQ(D2:D21) / СЧЁТ(D2:D21) )
- Поскольку мы уже вычислили разницу между прогнозируемыми и наблюдаемыми значениями в столбце D, мы можем вычислить сумму квадратов разностей с помощью функции SUMSQ(). функция только со значениями из столбца D.
- Затем мы делим набор данных на размер выборки с помощью COUNTA() , который подсчитывает количество непустых ячеек в диапазоне.
- Наконец, мы извлекаем квадратный корень из всего расчета с помощью функции КОРЕНЬ() .
Как интерпретировать RMSE
Как упоминалось ранее, RMSE — это полезный способ увидеть, насколько хорошо модель регрессии (или любая модель, производящая прогнозируемые значения) способна «подогнать» набор данных.
Чем больше RMSE, тем больше разница между прогнозируемыми и наблюдаемыми значениями, а это означает, что регрессионная модель хуже соответствует данным. И наоборот, чем меньше RMSE, тем лучше модель соответствует данным.
Может быть особенно полезно сравнить RMSE двух разных моделей, чтобы увидеть, какая модель лучше всего соответствует данным.
Дополнительные руководства по Excel можно найти на нашей странице «Руководства по Excel» , где перечислены все руководства по статистике в Excel.