Среднеквадратичное значение

К бенджамин андерсон 6 августа, 2023 Статистика 0 комментариев

Здесь мы объясним, что такое среднеквадратическое значение и как оно рассчитывается. Кроме того, вы узнаете преимущества и недостатки использования среднего и пошагово решаемого упражнения. Наконец, вы сможете вычислить среднеквадратическое значение любого набора данных с помощью калькулятора в конце статьи.

Что такое средний квадрат?

Среднеквадратичное значение является мерой центральности описательной статистики. Среднеквадратичное значение равно квадратному корню из среднего арифметического квадратов данных.

Среднеквадратическое значение также называют среднеквадратическим или RMS .

Таким образом, формула для среднего квадратичного значения выглядит следующим образом:

Среднее квадратическое особенно полезно, когда статистическая переменная принимает положительные и отрицательные значения, поскольку при возведении в квадрат каждого фрагмента данных все значения становятся положительными. Поэтому среднеквадратическое значение используют для анализа переменных, в которых важен не знак, а его абсолютное значение.

Например, среднеквадратичный метод используется для изучения ошибок измерения, поскольку в этих случаях мы не смотрим, является ли ошибка положительной или отрицательной, а анализируем величину ошибки при измерении.

Кроме того, квадраты больших чисел имеют гораздо более высокие значения, чем квадраты маленьких чисел, поэтому в среднем квадрате большие числа важнее маленьких.

Среднее квадратичное — это тип статистического среднего значения, наряду со средним арифметическим, средневзвешенным, средним геометрическим и средним гармоническим.

Преимущества и недостатки среднеквадратического метода

Среднее квадратичное имеет преимущества и недостатки по сравнению с другими типами средних.

Основное преимущество квадратичного среднего состоит в том, что оно позволяет получить очень хорошее приближение среднего значения дискретной переменной. С другой стороны, большим недостатком среднего квадрата является то, что его расчет достаточно сложен, поскольку необходимо выполнить несколько операций.

Напротив, среднеквадратическое значение очень полезно для анализа измерений ошибок. Это также придает гораздо большее значение высоким значениям, хотя это свойство подразумевает, что неправильное измерение значительно изменит среднеквадратичный результат.

Как вычислить среднеквадратичный корень

Для расчета среднеквадратического значения необходимо выполнить следующие действия:

Вычислите квадрат каждого статистического данных.
Сложите все квадраты, рассчитанные на предыдущем шаге.
Разделите результат на количество элементов данных в выборке.
Найдите квадратный корень из предыдущего значения.
Полученный результат представляет собой среднее квадратическое статистической выборки.

👉 Вы можете использовать калькулятор ниже, чтобы вычислить среднеквадратическое значение любого набора данных.

Среднеквадратичный пример

Как только мы узнаем, как получить среднеквадратическое значение, мы в качестве примера определим среднеквадратическое значение набора данных.

На занятиях в университетской лаборатории профессор просит своих студентов провести эксперимент с химическими веществами. Цель химического эксперимента – получить в общей сложности раствор объемом 3 л. Студенческие группы получили следующие данные:

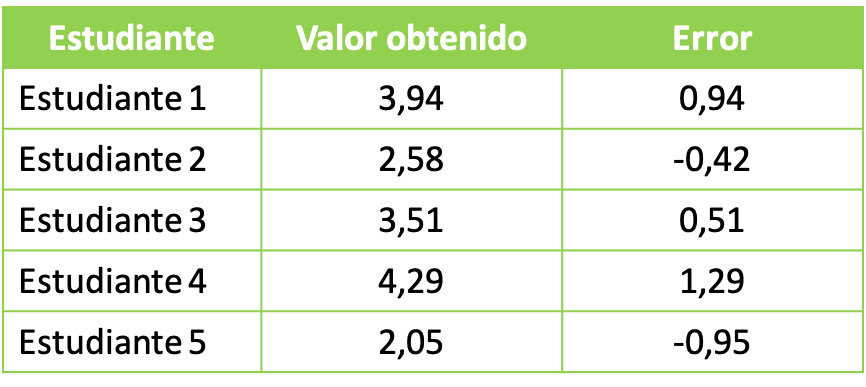
С целью изучения полученных статистических данных приступим к расчету значения среднего квадрата с погрешностью, полученной каждой группой. Поэтому мы применяем формулу среднего квадратичного:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

И подставляем данные в формулу и вычисляем среднеквадратическое значение:

$\displaystyle RMS=\sqrt{\frac{0,94^2+(-0,42)^2+0,51^2+1,29^2+(-0,95)^2}{5}}=0,88$

Таким образом, средняя ошибка, полученная в эксперименте, по среднеквадратичному значению составляет 0,88 литра.

Среднеквадратичный калькулятор

Введите данные из любой статистической выборки в следующий калькулятор, чтобы вычислить ее среднеквадратическое значение. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше