Среднее, медиана и мода
В этой статье объясняется, что такое среднее значение, медиана и мода. Вы узнаете, как получить среднее значение, медиану и моду, для чего они используются и в чем разница между этими тремя статистическими показателями. Кроме того, вы сможете рассчитать среднее значение, медиану и моду любой статистической выборки с помощью онлайн-калькулятора в конце.
Что такое среднее, медиана и мода?
Среднее значение, медиана и мода являются статистическими мерами центрального положения. Другими словами, среднее значение, медиана и мода — это значения, которые помогают определить статистическую выборку, в частности, они указывают, каковы ее центральные значения.
Среднее значение, медиана и мода определяются следующим образом:
- Среднее : среднее значение всех данных в выборке.
- Медиана : это среднее значение всех данных, упорядоченных от наименьшего к наибольшему.
- Режим : это наиболее повторяющееся значение в наборе данных.
Эти три статистических показателя более подробно объяснены ниже.
Половина
Чтобы вычислить среднее значение, сложите все значения, а затем разделите их на общее количество данных. Таким образом, формула среднего значения выглядит следующим образом:

👉 Вы можете использовать калькулятор ниже, чтобы рассчитать среднее, медиану и моду любого набора данных.
Средний символ — горизонтальная полоса над буквой х.
![]()
Вы также можете отличить среднее значение выборки от среднего значения генеральной совокупности с помощью символа среднего: среднее значение выборки выражается символом
![]()
, тогда как в среднем население использует греческую букву
![]()
Среднее значение также известно как среднее арифметическое или среднее значение . Более того, среднее значение статистического распределения эквивалентно его математическому ожиданию.
Средний пример
- За учебный год учащийся получил следующие оценки: по математике — 9, по языку — 7, по истории — 6, по экономике — 8 и по естественным наукам — 7,5. Каково среднее значение всех ваших оценок?
Чтобы найти среднее арифметическое, нам нужно сложить все оценки, а затем разделить на общее количество предметов в курсе, которое равно 5. Поэтому применим формулу среднего арифметического:

Подставляем данные в формулу и вычисляем среднее арифметическое:
![]()
Как видите, в среднем арифметическом каждому значению присваивается одинаковый вес, то есть каждый фрагмент данных имеет одинаковый вес в целом.
медиана
Медиана — это среднее значение всех данных, упорядоченных от наименьшего к наибольшему. Другими словами, медиана делит упорядоченный набор данных на две равные части.
Расчет медианы зависит от того, является ли общее количество данных четным или нечетным:
- Если общее количество данных нечетное , медианой будет значение, попадающее прямо в середину данных. То есть значение, которое находится в позиции (n+1)/2 отсортированных данных.
- Если общее количество точек данных четное , медиана будет средним значением двух точек данных, расположенных в центре. То есть среднее арифметическое значений, которые находятся в позициях n/2 и n/2+1 упорядоченных данных.
![]()
![]()
Золото
![]()
— общее количество элементов данных в выборке.
Термин Me часто используется как символ, обозначающий, что значение является медианным всех наблюдений.
👉 Вы можете использовать калькулятор ниже, чтобы рассчитать среднее, медиану и моду любого набора данных.
Медианный пример
- Найдите медиану следующих данных: 3, 4, 1, 6, 7, 4, 8, 2, 8, 4, 5.
Первое, что нужно сделать, прежде чем приступить к расчетам, это классифицировать данные, то есть расставить числа от меньшего к большему.
![]()
В данном случае у нас 11 наблюдений, поэтому общее количество данных нечетное. Поэтому мы применяем следующую формулу для расчета положения медианы:
![]()
Таким образом, медианой будут данные, расположенные на шестой позиции, что в данном случае соответствует значению 4.
![]()
Мода
В статистике мода — это значение в наборе данных, имеющее наибольшую абсолютную частоту, то есть мода — это наиболее повторяющееся значение в наборе данных.
Поэтому, чтобы вычислить моду набора статистических данных, просто подсчитайте, сколько раз каждый элемент данных появляется в выборке, и наиболее повторяющиеся данные будут модой.
Этот режим также можно назвать статистическим режимом или модальным значением . Аналогичным образом, когда данные группируются по интервалам, наиболее повторяющийся интервал — это модальный интервал или модальный класс .
В общем, термин Mo используется как символ статистического режима, например, режим распределения X представляет собой Mo(X).
По количеству наиболее повторяющихся значений можно выделить три типа режимов:
- Унимодальный режим : имеется только одно значение с максимальным количеством повторений. Например, [1, 4, 2, 4, 5, 3].
- Бимодальный режим : максимальное количество повторов происходит при двух разных значениях, и оба значения повторяются одинаковое количество раз. Например, [2, 6, 7, 2, 3, 6, 9].
- Мультимодальный режим : три и более значений имеют одинаковое максимальное количество повторений. Например, [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1].
👉 Вы можете использовать калькулятор ниже, чтобы рассчитать среднее, медиану и моду любого набора данных.
пример моды
- Каков режим следующего набора данных?
![]()
Числа не в порядке, поэтому первое, что мы сделаем, это отсортируем их. Этот шаг не является обязательным, но он поможет вам легче находить моду.
![]()
Цифры 2 и 9 встречаются дважды, а цифра 5 повторяется три раза. Следовательно, мода ряда данных имеет номер 5.
![]()
Решенное упражнение для среднего, медианы и моды
Теперь, когда вы знаете, что такое среднее значение, медиана и мода, ниже приведено подробное упражнение по этим статистическим показателям, чтобы вы могли точно увидеть, как они рассчитываются.
- Найдите среднее значение, медиану и моду следующего набора статистических данных:
![]()
![]()
Чтобы найти среднее значение данных, нам нужно все это сложить, а затем разделить на общее количество данных, равное 30:
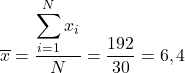
Во-вторых, давайте выясним выборочную медиану. Итак, расположим все числа в порядке возрастания:
![]()
![]()
В этом случае общее количество данных четное, поэтому необходимо вычислить две центральные позиции, между которыми будет найдена медиана. Для этого воспользуемся следующими двумя формулами:
![]()
![]()
Таким образом, медиана будет находиться между пятнадцатой и шестнадцатой позицией, что соответствует значениям 6 и 7 соответственно. Точнее, медиана эквивалентна среднему значению этих значений:
![]()
Наконец, чтобы найти режим, вам просто нужно посчитать, сколько раз появляется каждое число. Как видите, всего цифры 6 и 8 встречаются четыре раза, что является максимальным количеством повторений. Следовательно, в данном случае это бимодальный режим, а два числа — это режим набора данных:
![]()
Калькулятор среднего, медианного значения и режима
Введите данные из любой статистической выборки в следующий онлайн-калькулятор, чтобы рассчитать ее среднее значение, медиану и моду. Данные должны быть разделены пробелом и введены с использованием точки в качестве десятичного разделителя.