Как рассчитать sst, ssr и sse в excel
Мы часто используем три разные суммы квадратов , чтобы измерить, насколько хорошо линия регрессии соответствует набору данных:
1. Сумма общих квадратов (SST) – сумма квадратов разностей между отдельными точками данных (y i ) и средним значением переменной ответа ( y ).
- SST = Σ(y i – y ) 2
2. Регрессия суммы квадратов (SSR) – сумма квадратов разностей между прогнозируемыми точками данных (ŷ i ) и средним значением переменной ответа ( y ).
- ССР = Σ(ŷ i – y ) 2
3. Ошибка суммы квадратов (SSE) – сумма квадратов разностей между прогнозируемыми точками данных (ŷ i ) и наблюдаемыми точками данных (y i ).
- SSE = Σ(ŷ i – y i ) 2
В следующем пошаговом примере показано, как вычислить каждую из этих метрик для заданной модели регрессии в Excel.
Шаг 1. Создайте данные
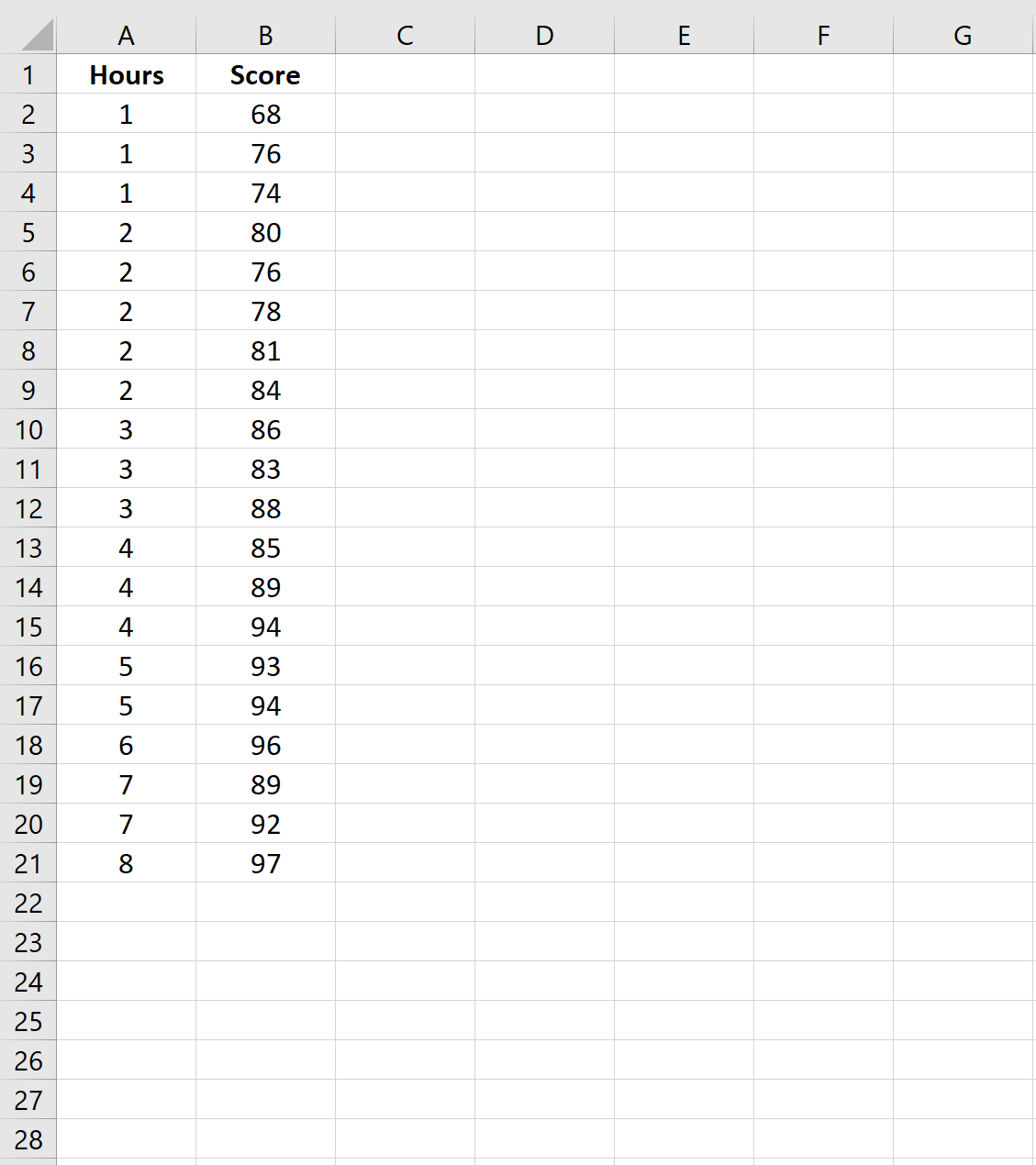
Сначала давайте создадим набор данных, содержащий количество учебных часов и результаты экзаменов, полученные 20 разными учениками в данной школе:
Шаг 2. Подберите регрессионную модель
На верхней ленте Excel перейдите на вкладку «Данные» и нажмите «Анализ данных» . Если вы не видите эту опцию, вам необходимо сначала установить бесплатное программное обеспечение Analysis ToolPak .

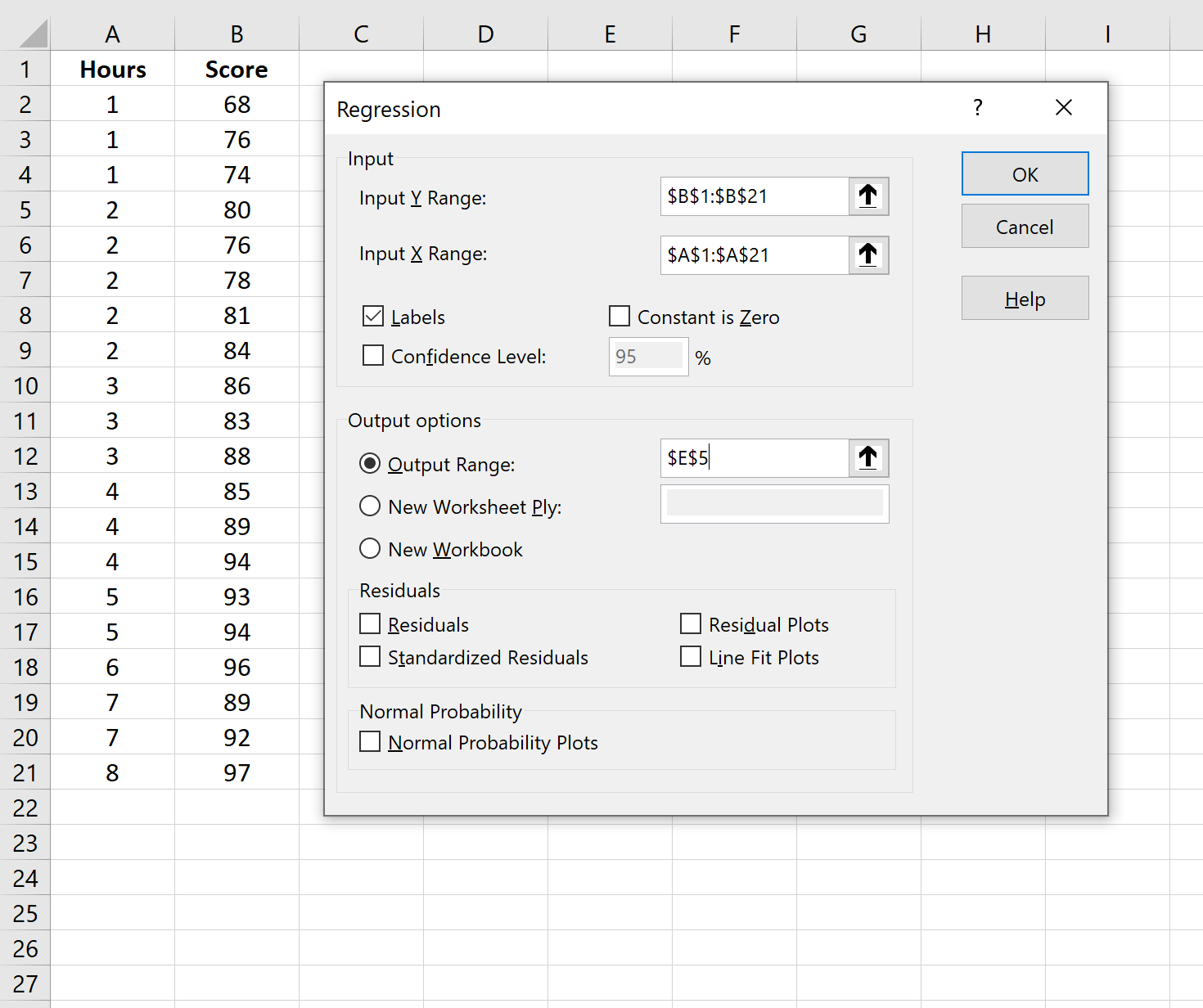
После того, как вы нажмете «Анализ данных», появится новое окно. Выберите «Регрессия» и нажмите «ОК».
В появившемся новом окне укажите следующую информацию:
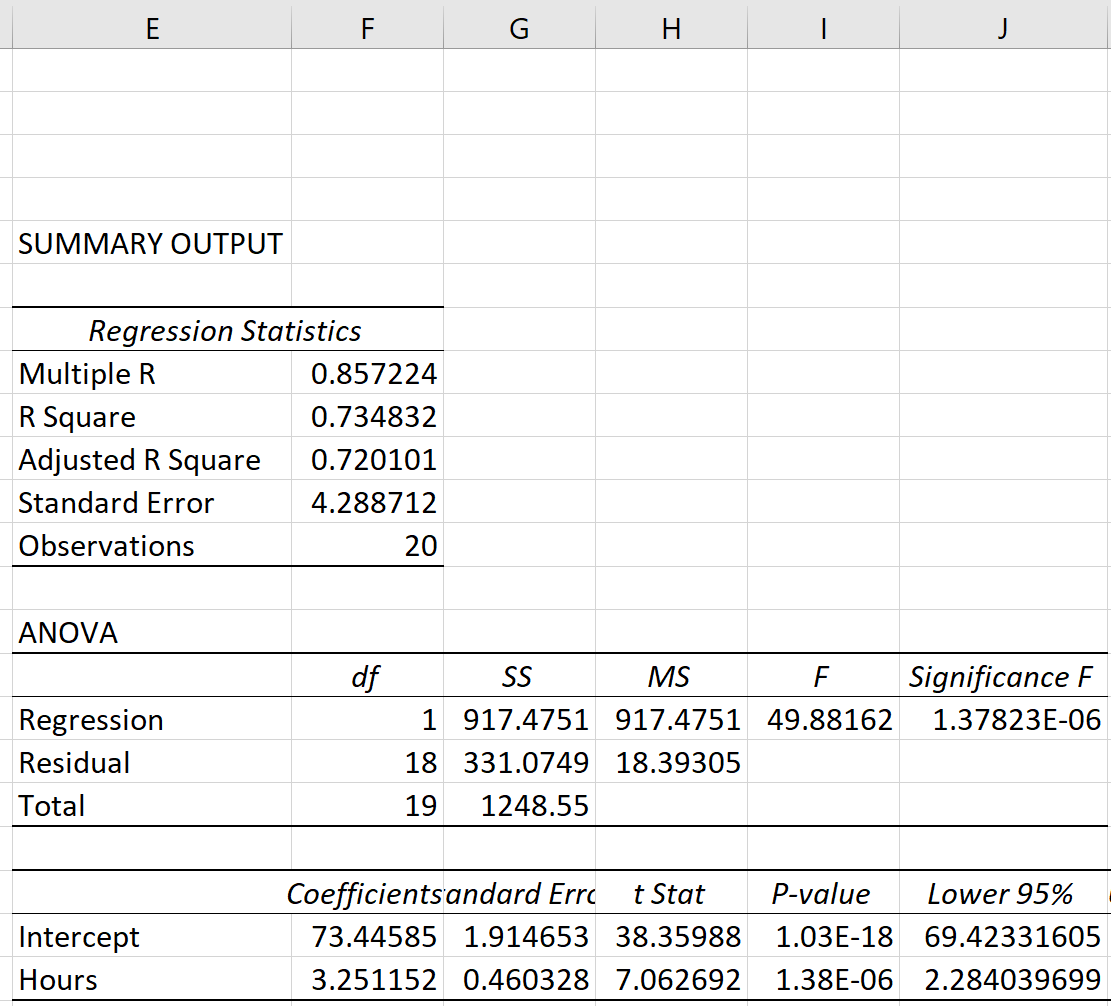
Как только вы нажмете «ОК» , появятся выходные данные регрессии.
Шаг 3: Проанализируйте результат
Три показателя суммы квадратов — SST, SSR и SSE — можно увидеть в столбце SS таблицы ANOVA :
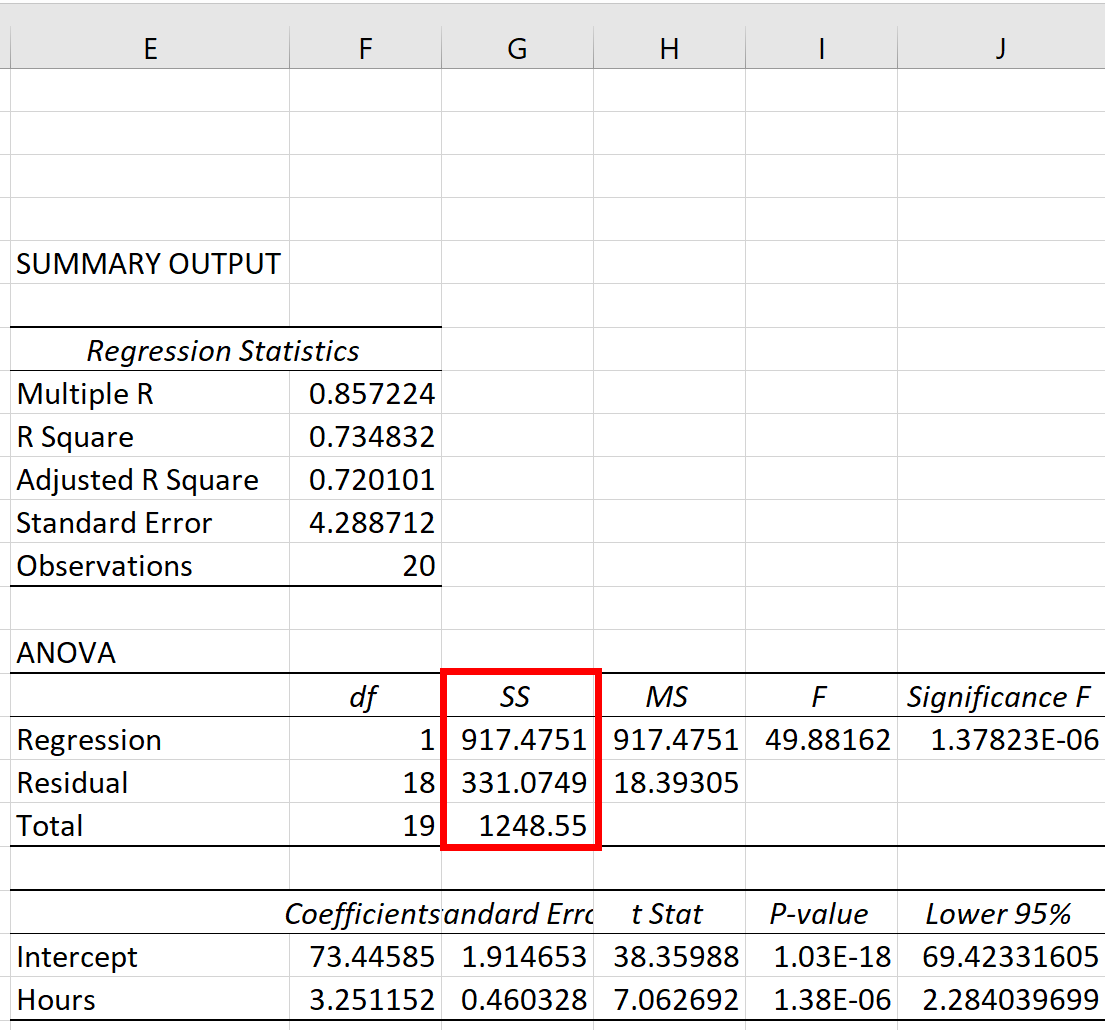
Метрики оказываются такими:
- Общая сумма квадратов (SST): 1248,55
- Регрессия суммы квадратов (SSR): 917,4751
- Ошибка суммы квадратов (SSE): 331,0749.
Мы можем проверить, что SST = SSR + SSE:
- ССТ = ССР + ССЕ
- 1248,55 = 917,4751 + 331,0749
Мы также можем вручную рассчитать R-квадрат регрессионной модели:
- R в квадрате = ССР/ССТ
- R в квадрате = 917,4751/1248,55
- R в квадрате = 0,7348
Это говорит нам о том, что 73,48% различий в результатах экзаменов можно объяснить количеством изученных часов.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Excel
Как выполнить множественную линейную регрессию в Excel
Как выполнить полиномиальную регрессию в Excel
Как выполнить экспоненциальную регрессию в Excel