Нежный путеводитель по сумме квадратов: sst, ssr, sse
Линейная регрессия используется для поиска линии, которая лучше всего «соответствует» набору данных.
Мы часто используем три разные суммы квадратов , чтобы измерить, насколько хорошо линия регрессии соответствует данным:
1. Сумма общих квадратов (SST) – сумма квадратов разностей между отдельными точками данных (y i ) и средним значением переменной ответа ( y ).
- SST = Σ(y i – y ) 2
2. Регрессия суммы квадратов (SSR) – сумма квадратов разностей между прогнозируемыми точками данных (ŷ i ) и средним значением переменной ответа ( y ).
- ССР = Σ(ŷ i – y ) 2
3. Ошибка суммы квадратов (SSE) – сумма квадратов разностей между прогнозируемыми точками данных (ŷ i ) и наблюдаемыми точками данных (y i ).
- SSE = Σ(ŷ i – y i ) 2
Между этими тремя показателями существует следующая связь:
ССТ = ССР + ССЕ
Итак, если мы знаем два из этих измерений, мы можем использовать простую алгебру для вычисления третьего.
ССР, ССТ и R-площадь
R-квадрат , иногда называемый коэффициентом детерминации, является мерой того, насколько хорошо модель линейной регрессии соответствует набору данных. Он представляет собой долю дисперсии переменной ответа , которую можно объяснить переменной-предиктором.
Значение R-квадрата может находиться в диапазоне от 0 до 1. Значение 0 указывает на то, что переменная ответа вообще не может быть объяснена переменной-предиктором. Значение 1 указывает на то, что переменная ответа может быть полностью без ошибок объяснена переменной-предиктором.
Используя SSR и SST, мы можем вычислить R в квадрате следующим образом:
R в квадрате = ССР/ССТ
Например, если SSR для данной регрессионной модели равен 137,5, а SST — 156, мы бы вычислили R в квадрате следующим образом:
R в квадрате = 137,5/156 = 0,8814
Это говорит нам о том, что 88,14% вариаций переменной ответа можно объяснить переменной-предиктором.
Рассчитать SST, SSR, SSE: пошаговый пример
Предположим, у нас есть следующий набор данных, который показывает количество часов, изученных шестью разными студентами, а также их итоговые оценки на экзамене:
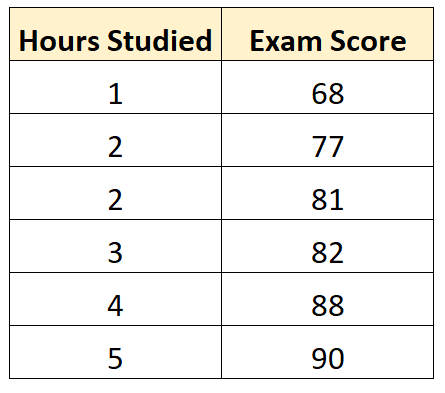
Используя какое-нибудь статистическое программное обеспечение (например, R , Excel , Python ) или даже вручную, мы видим, что наиболее подходящая линия:
Оценка = 66,615 + 5,0769*(Часы)
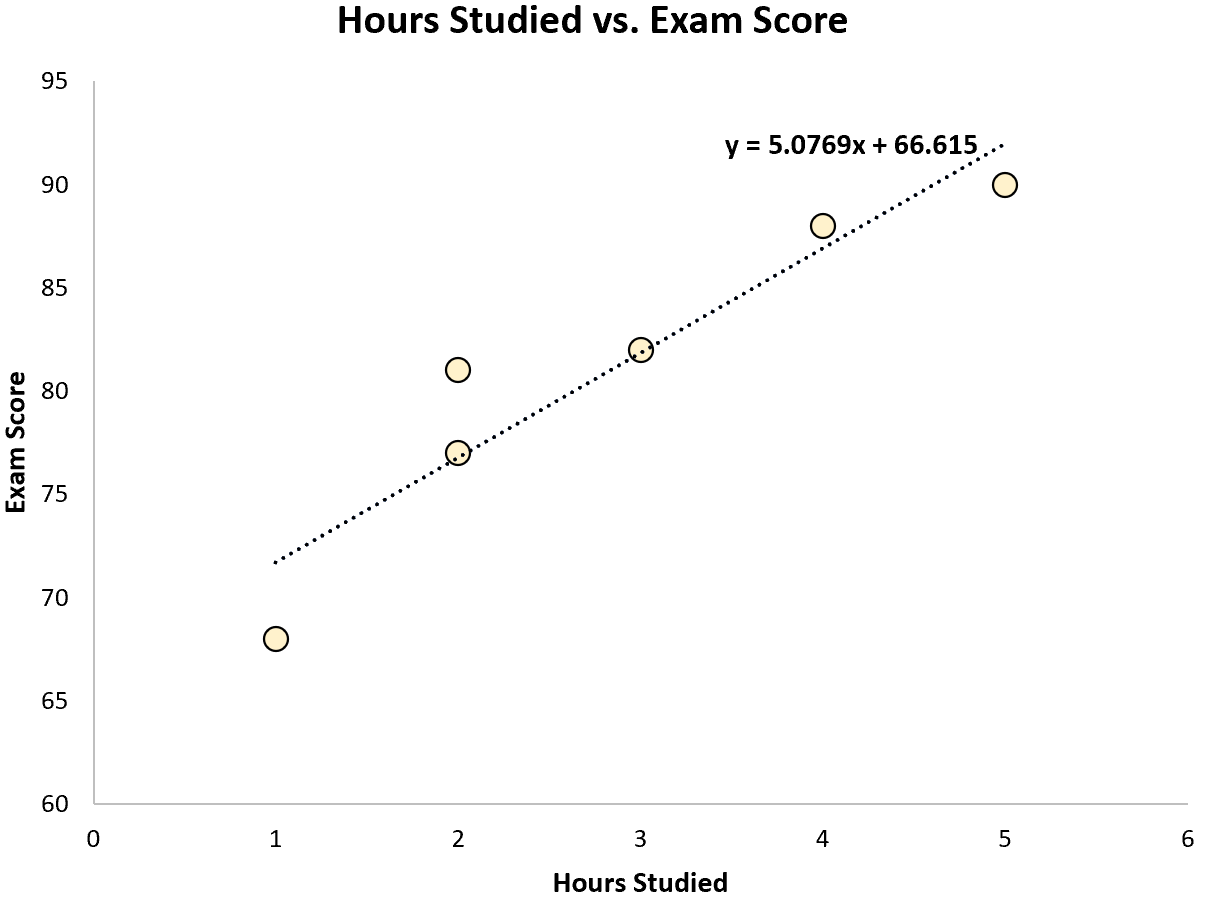
Как только мы узнаем линию наилучшего уравнения, мы можем использовать следующие шаги для расчета SST, SSR и SSE:
Шаг 1: Рассчитайте среднее значение переменной ответа.
Среднее значение переменной ответа ( y ) оказывается равным 81 .
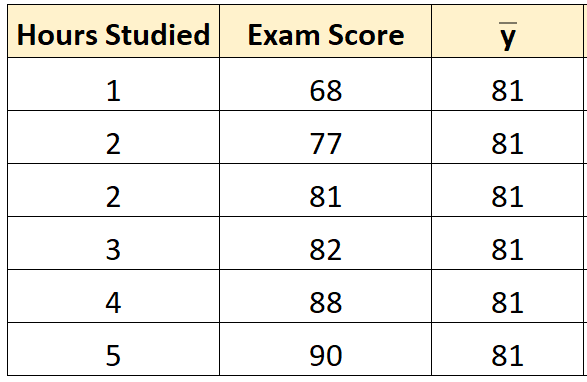
Шаг 2: Рассчитайте прогнозируемое значение для каждого наблюдения.
Затем мы можем использовать строку уравнения наилучшего соответствия для расчета прогнозируемого результата экзамена () для каждого студента.
Например, прогнозируемая оценка на экзамене для студента, проучившегося один час:
Оценка = 66,615 + 5,0769*(1) = 71,69 .
Мы можем использовать тот же подход, чтобы найти прогнозируемый балл для каждого учащегося:
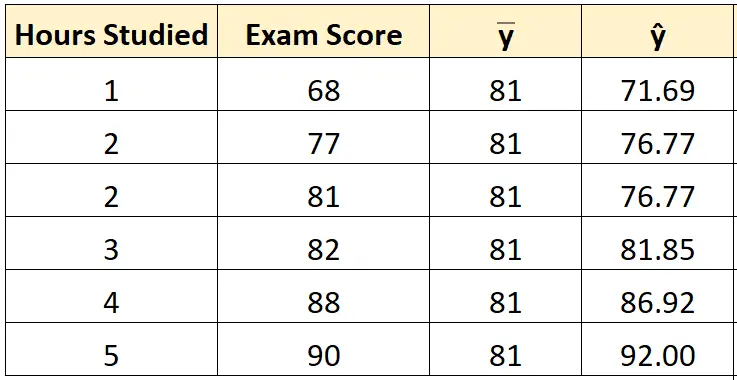
Шаг 3: Рассчитайте общую сумму квадратов (SST).
Тогда мы можем вычислить сумму квадратов в целом.
Например, общая сумма квадратов для первого ученика равна:
(y i – y ) 2 = (68 – 81) 2 = 169 .
Мы можем использовать тот же подход, чтобы найти общую сумму квадратов для каждого ученика:
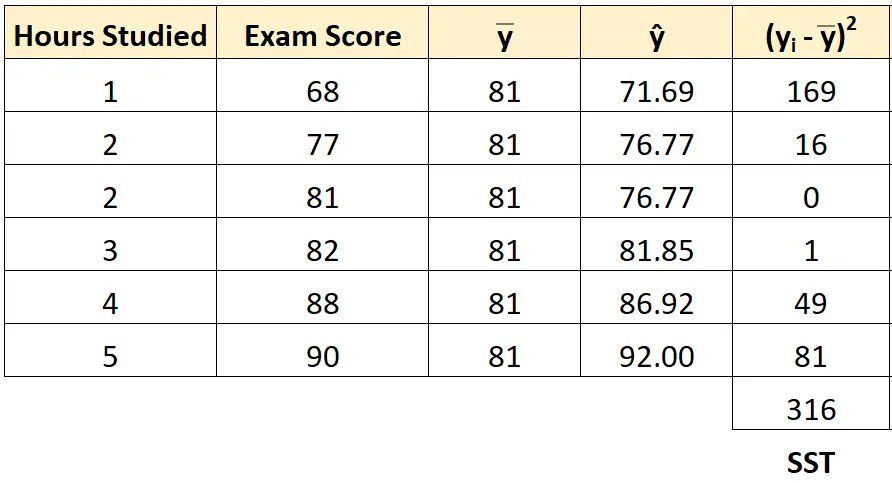
Общая сумма квадратов оказывается 316 .
Шаг 4: Рассчитайте регрессию суммы квадратов (SSR).
Затем мы можем рассчитать регрессию суммы квадратов.
Например, регрессия суммы квадратов для первого студента:
( ŷi – y ) 2 = (71,69 – 81) 2 = 86,64 .
Мы можем использовать тот же подход, чтобы найти регрессию суммы квадратов для каждого ученика:
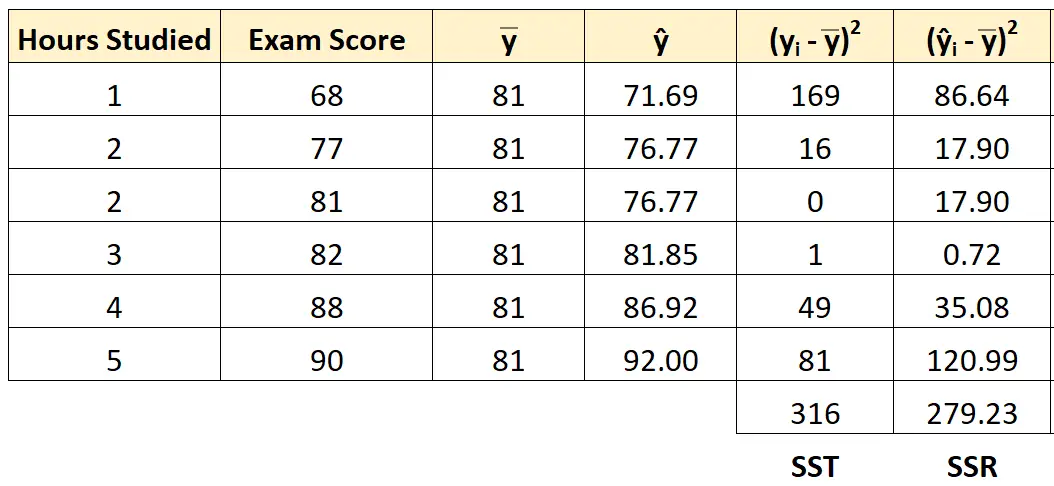
Сумма квадратов регрессии оказывается равной 279,23 .
Шаг 5: Рассчитайте ошибку суммы квадратов (SSE).
Тогда мы сможем вычислить погрешность суммы квадратов.
Например, ошибка суммы квадратов для первого ученика равна:
(ŷ i – y i ) 2 = (71,69 – 68) 2 = 13,63 .
Мы можем использовать тот же подход, чтобы найти сумму ошибок квадратов для каждого ученика:
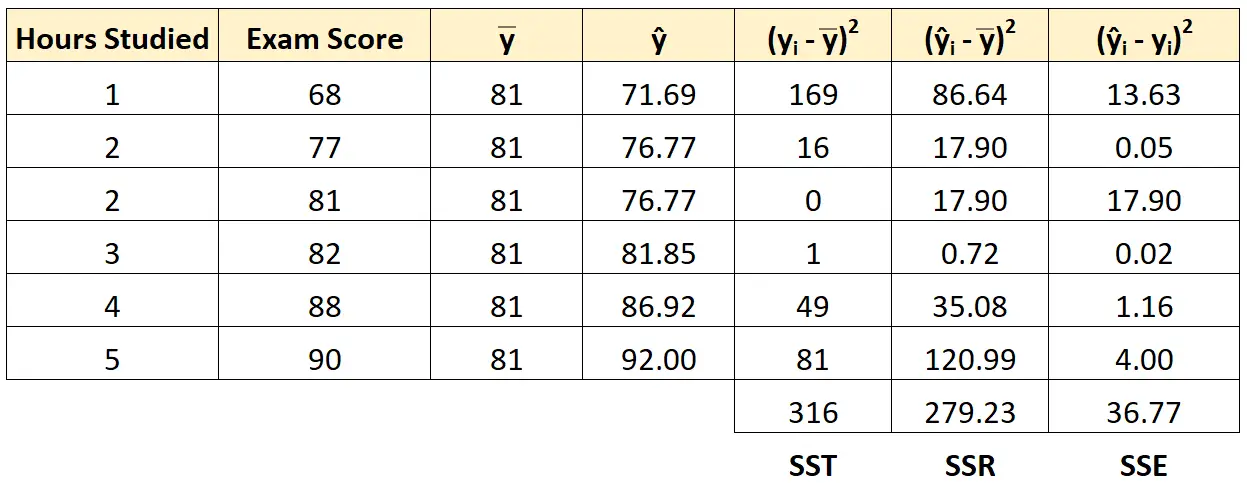
Мы можем проверить, что SST = SSR + SSE.
- ССТ = ССР + ССЕ
- 316 = 279,23 + 36,77
Мы также можем рассчитать R-квадрат регрессионной модели, используя следующее уравнение:
- R в квадрате = ССР/ССТ
- R в квадрате = 279,23/316
- R в квадрате = 0,8836
Это говорит нам о том, что 88,36% различий в результатах экзаменов можно объяснить количеством изученных часов.
Дополнительные ресурсы
Вы можете использовать следующие калькуляторы для автоматического расчета SST, SSR и SSE для любой простой линии линейной регрессии:
Калькулятор ССТ
RSS-калькулятор
Калькулятор ЕСС