Стандартизация или нормализация: в чем разница?

Стандартизация и нормализация — это два способа изменения размера данных.

Нормализация масштабирует набор данных так, чтобы оно имело среднее значение 0 и стандартное отклонение 1. Для этого используется следующая формула:

x _новый = (x _i – x ) / с

Золото:

• x _i : ^i-е значение набора данных
• x : Образец означает
• s : стандартное отклонение выборки

Нормализация изменяет размер набора данных так, чтобы каждое значение было в диапазоне от 0 до 1. Это делается с помощью следующей формулы:

x _новый = (x _i – x _min ) / (x _max – x _min )

Золото:

• x _i : ^i-е значение набора данных
• x _min : минимальное значение в наборе данных.
• x _max : максимальное значение в наборе данных.

Следующие примеры показывают, как на практике стандартизировать и нормализовать набор данных.

Пример: Как стандартизировать данные

Предположим, у нас есть следующий набор данных:

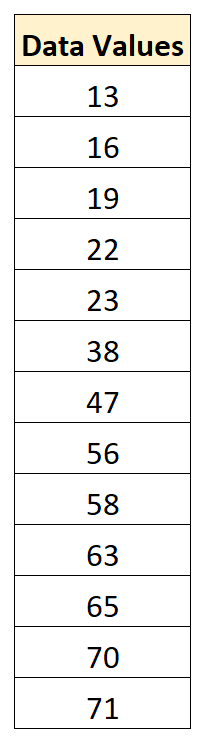
Среднее значение в наборе данных составляет 43,15, а стандартное отклонение — 22,13.

Чтобы нормализовать первое значение 13 , мы бы применили ранее использованную формулу:

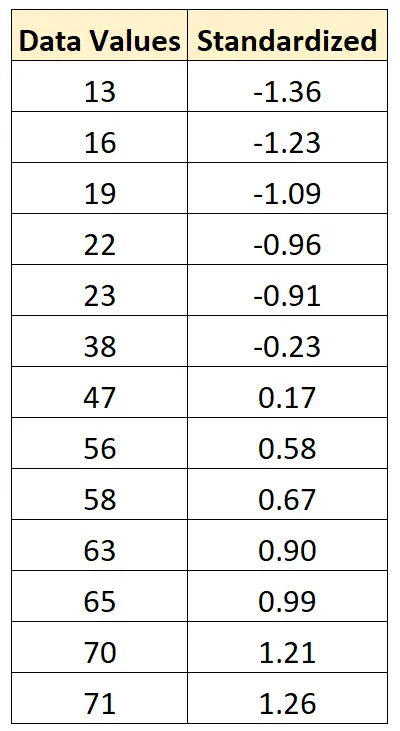
• x _новый = (x _i – x )/s = (13 – 43,15)/22,13 = -1,36

Чтобы нормализовать второе значение 16 , мы будем использовать ту же формулу:

• x _новый = (x _i – x )/s = (16 – 43,15)/22,13 = -1,23

Чтобы нормализовать третье значение 19 , мы будем использовать ту же формулу:

• x _новый = (x _i – x )/s = (19 – 43,15)/22,13 = -1,09

Мы можем использовать ту же самую формулу для стандартизации каждого значения в исходном наборе данных:

Пример: Как нормализовать данные

Опять же, предположим, что у нас есть следующий набор данных:

Минимальное значение в наборе данных — 13, а максимальное — 71.

Чтобы нормализовать первое значение 13 , мы бы применили ранее использованную формулу:

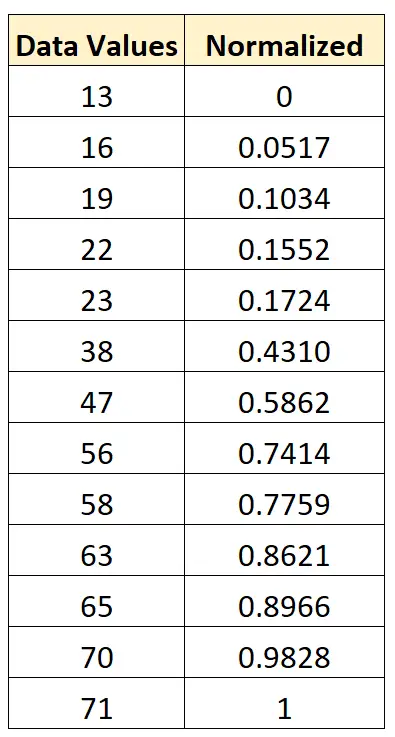
• x _new = (x _i – x _min ) / (x _max – x _min ) = (13 – 13) / (71 – 13) = 0

Чтобы нормализовать второе значение 16 , мы будем использовать ту же формулу:

• x _new = (x _i – x _min ) / (x _max – x _min ) = (16 – 13) / (71 – 13) = 0,0517

Чтобы нормализовать третье значение 19 , мы будем использовать ту же формулу:

• x _new = (x _i – x _min ) / (x _max – x _min ) = (19 – 13) / (71 – 13) = 0,1034

Мы можем использовать ту же самую формулу для нормализации каждого значения в исходном наборе данных между 0 и 1:

Стандартизация или нормализация: когда их использовать?

Обычно мы нормализуем данные, когда проводим какой-либо анализ, в котором у нас есть несколько переменных, измеренных в разных масштабах, и мы хотим, чтобы каждая из переменных имела один и тот же диапазон.

Это предотвращает неправомерное влияние одной переменной, особенно если она измеряется в разных единицах измерения (т. е. если одна переменная измеряется в дюймах, а другая в ярдах).

С другой стороны, мы обычно нормализуем данные, когда хотим узнать, на сколько стандартных отклонений каждое значение в наборе данных отличается от среднего.

Например, у нас может быть список результатов экзаменов для 500 учащихся определенной школы, и мы хотели бы знать, сколько стандартных отклонений каждый результат экзамена составляет от среднего балла.

В этом случае мы могли бы нормализовать необработанные данные, чтобы узнать эту информацию. Тогда стандартизированный балл 1,26 будет говорить нам, что экзаменационный балл этого конкретного студента на 1,26 стандартного отклонения выше среднего экзаменационного балла.

Если вы решите нормализовать или стандартизировать свои данные, имейте в виду следующие моменты:

• Нормализованный набор данных всегда будет иметь значения от 0 до 1.
• Стандартизированный набор данных будет иметь среднее значение 0 и стандартное отклонение 1, но не существует конкретного верхнего или нижнего предела для максимального и минимального значений.

В зависимости от вашего конкретного сценария может иметь смысл нормализовать или стандартизировать данные.

Дополнительные ресурсы

В следующих руководствах объясняется, как стандартизировать и нормализовать данные в различных статистических программах:

Как нормализовать данные в R
Как нормализовать данные в Excel
Как нормализовать данные в Python
Как стандартизировать данные в R