Как рассчитать стандартную ошибку среднего значения в excel
Стандартная ошибка среднего — это способ измерения распределения значений в наборе данных. Он рассчитывается следующим образом:
Стандартная ошибка = s / √n
Золото:
- s : выборочное стандартное отклонение
- n : размер выборки
Вы можете рассчитать стандартную ошибку среднего значения любого набора данных в Excel, используя следующую формулу:
= STDEV (диапазон значений) / SQRT ( COUNT (диапазон значений))
В следующем примере показано, как использовать эту формулу.
Пример: стандартная ошибка в Excel
Предположим, у нас есть следующий набор данных:
На следующем снимке экрана показано, как рассчитать стандартную ошибку среднего значения для этого набора данных:
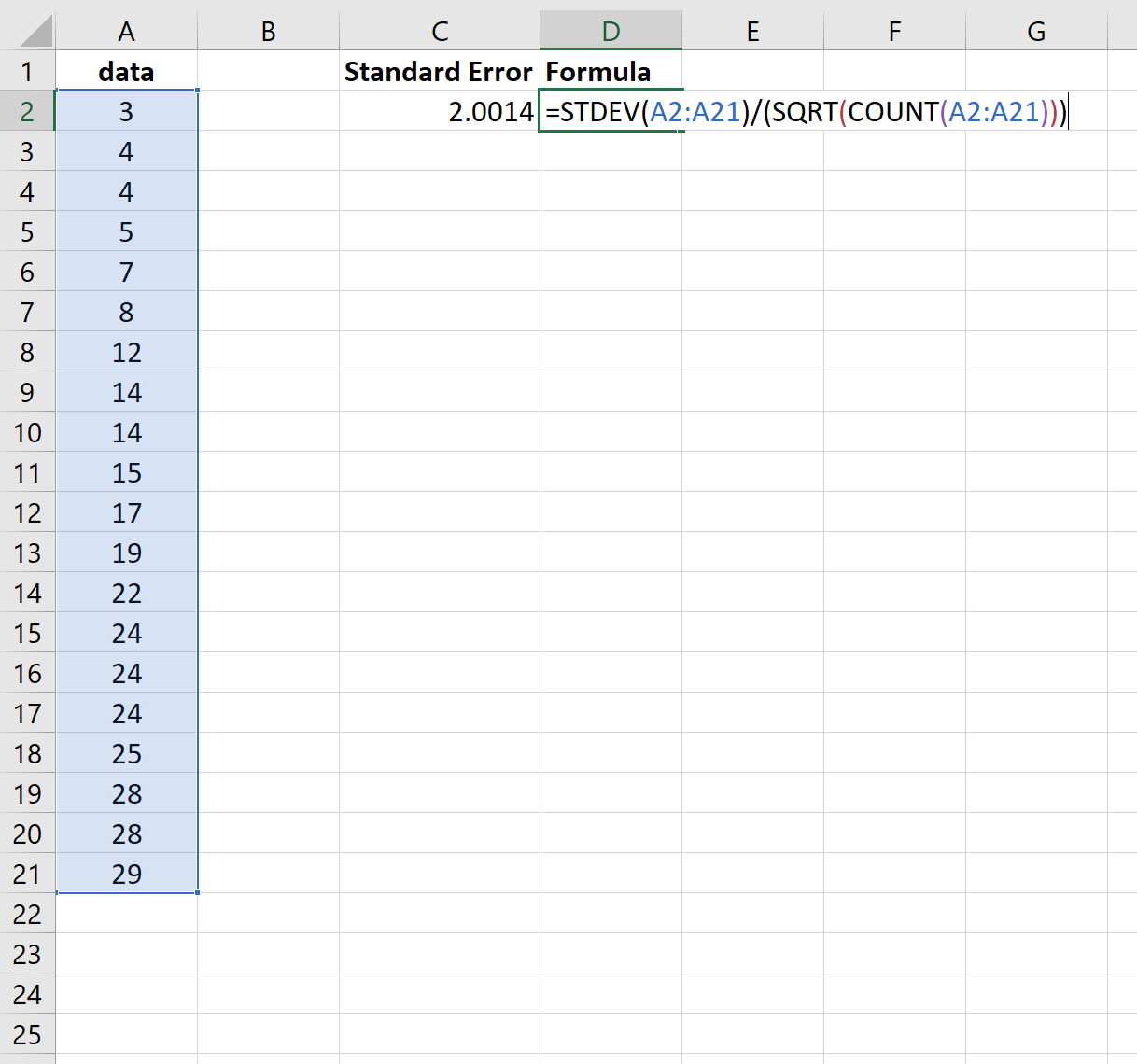
Стандартная ошибка оказывается 2,0014 .
Обратите внимание, что функция =STDEV() вычисляет выборочное среднее значение, что эквивалентно функции =STDEV.S() в Excel.
Итак, мы могли бы использовать следующую формулу для получения тех же результатов:
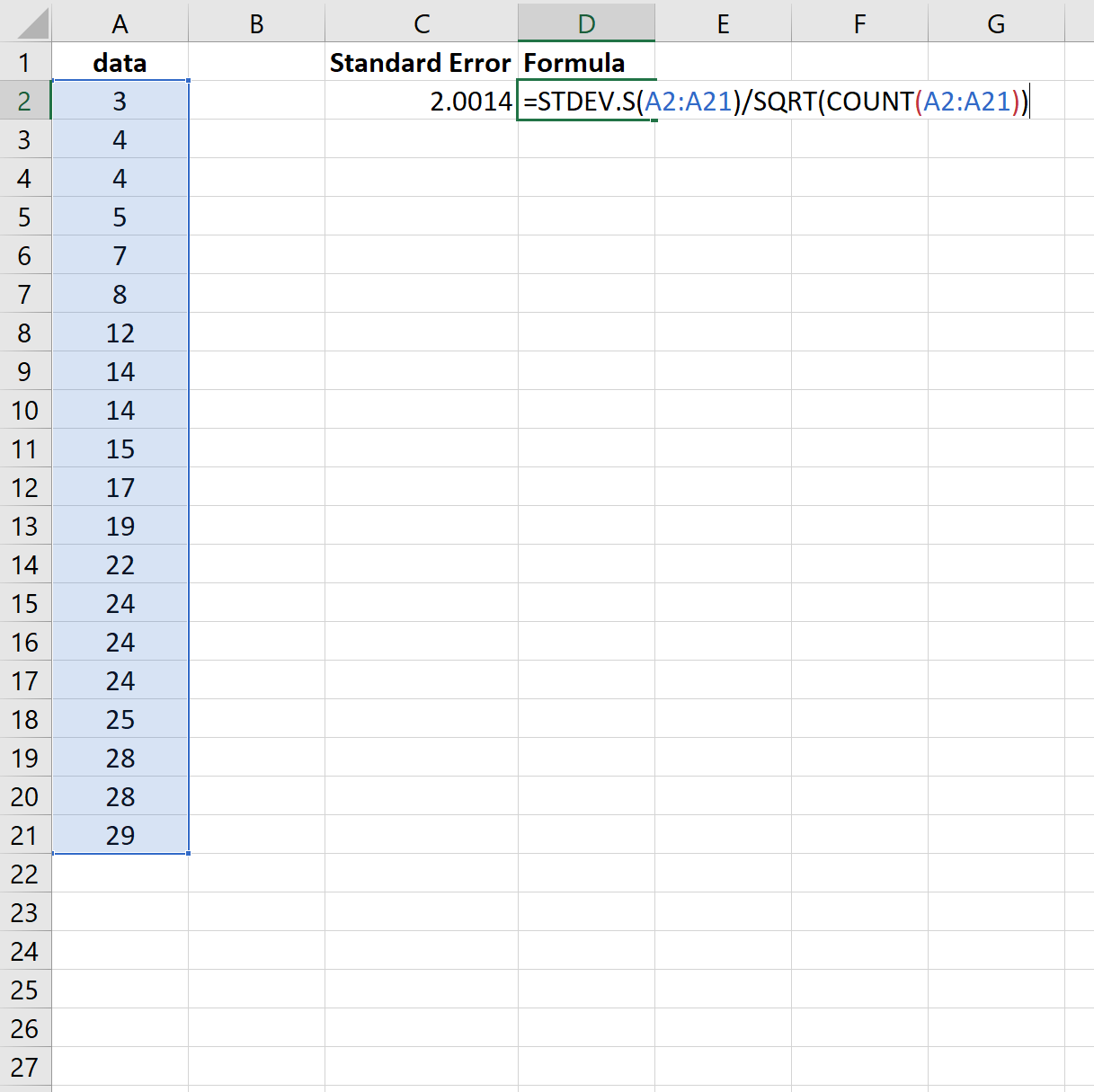
И снова стандартная ошибка оказывается 2.0014 .
Как интерпретировать стандартную ошибку среднего значения
Стандартная ошибка среднего — это просто мера разброса значений вокруг среднего. При интерпретации стандартной ошибки среднего значения следует иметь в виду две вещи:
1. Чем больше стандартная ошибка среднего, тем более разбросаны значения вокруг среднего в наборе данных.
Чтобы проиллюстрировать это, рассмотрим, изменим ли мы последнее значение предыдущего набора данных на гораздо большее число:
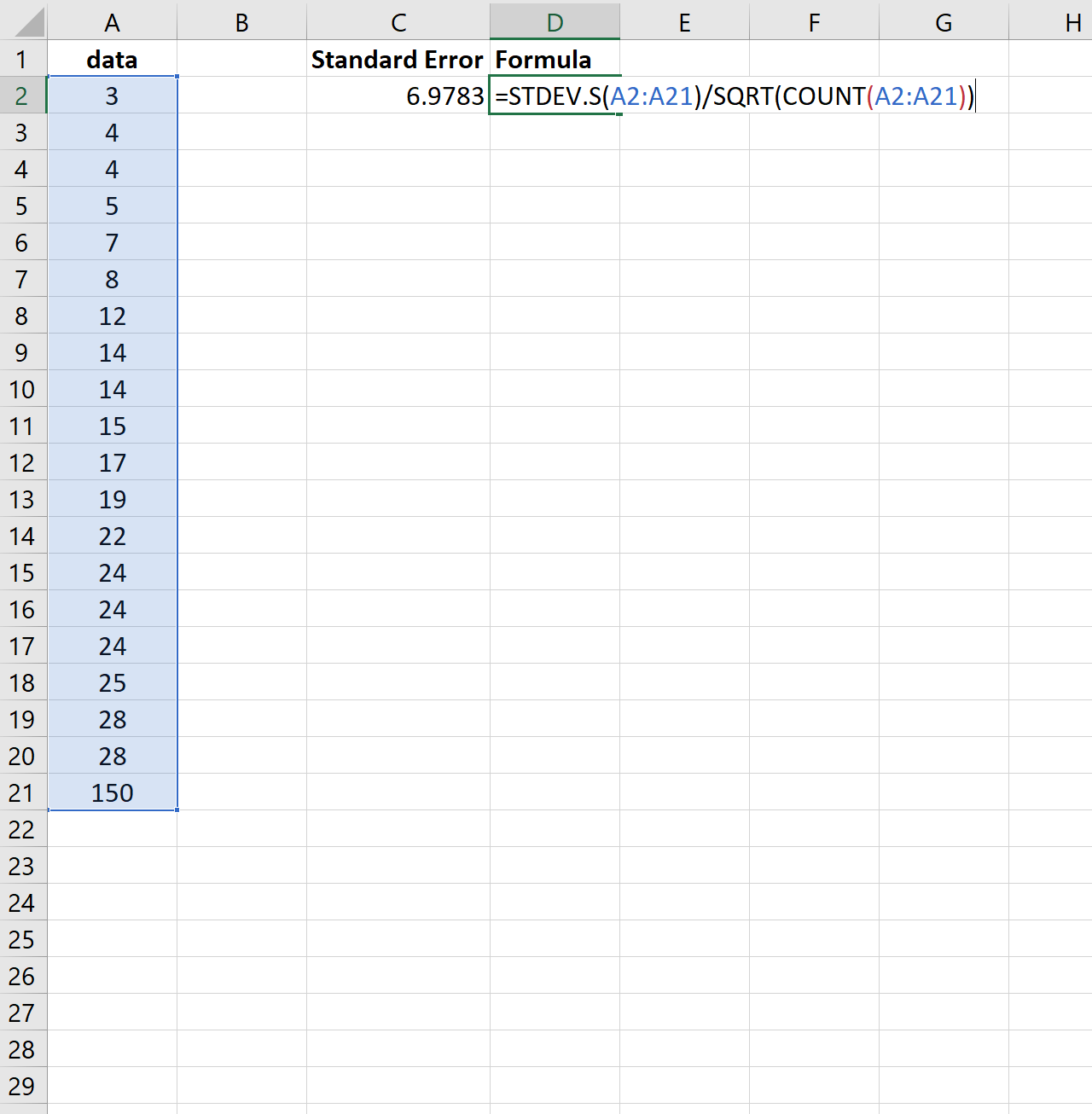
Обратите внимание, как стандартная ошибка увеличивается с 2,0014 до 6,9783 . Это указывает на то, что значения в этом наборе данных больше распределены вокруг среднего значения по сравнению с предыдущим набором данных.
2. По мере увеличения размера выборки стандартная ошибка среднего имеет тенденцию к уменьшению.
Чтобы проиллюстрировать это, рассмотрим стандартную ошибку среднего значения для следующих двух наборов данных:
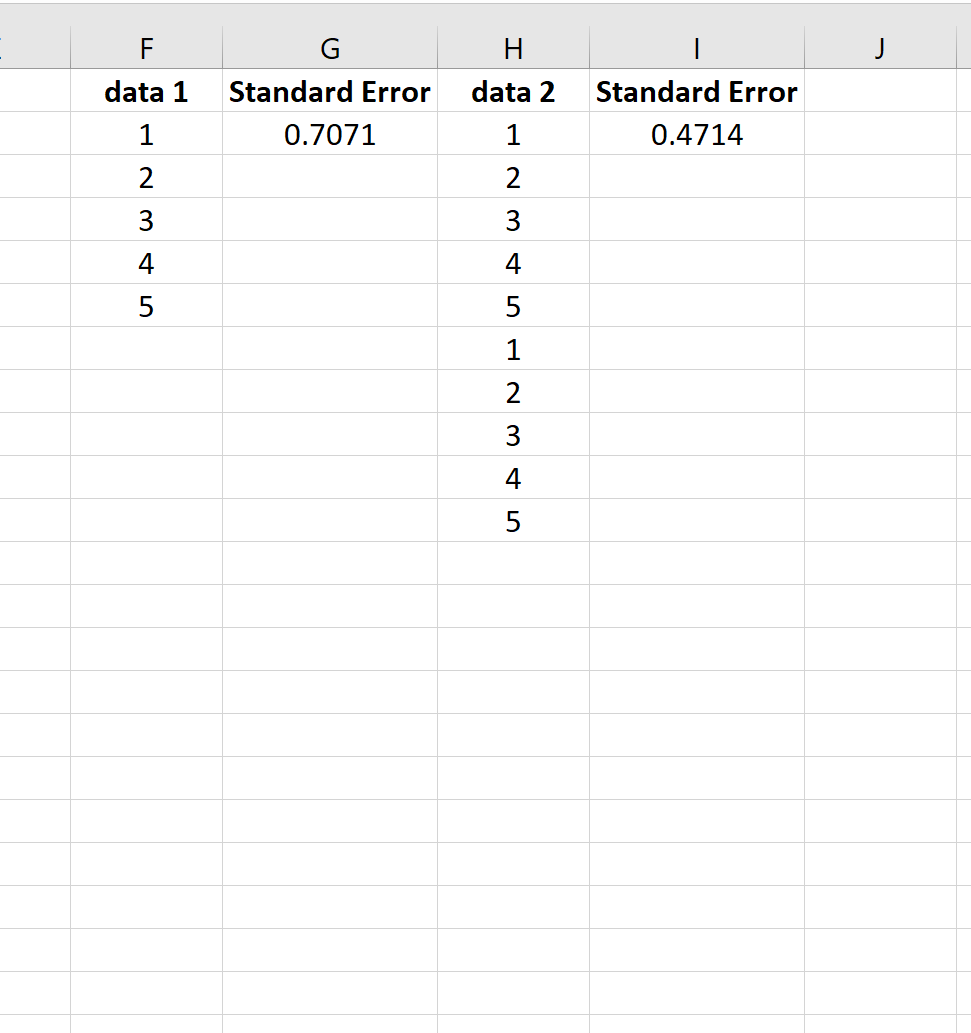
Второй набор данных — это просто первый набор данных, повторенный дважды. Таким образом, оба набора данных имеют одинаковое среднее значение, но второй набор данных имеет больший размер выборки и, следовательно, имеет меньшую стандартную ошибку.