Как рассчитать стандартную ошибку регрессии в excel
Мы подбираем модель линейной регрессии , модель принимает следующий вид:
Y = β 0 + β 1 X + … + β я
где ϵ — член ошибки, не зависящий от X.
Независимо от того, как X можно использовать для прогнозирования значений Y, в модели всегда будет случайная ошибка.
Один из способов измерения дисперсии этой случайной ошибки — использовать стандартную ошибку регрессионной модели , которая представляет собой способ измерения стандартного отклонения остатков ϵ.
В этом руководстве представлен пошаговый пример расчета стандартной ошибки регрессионной модели в Excel.
Шаг 1. Создайте данные
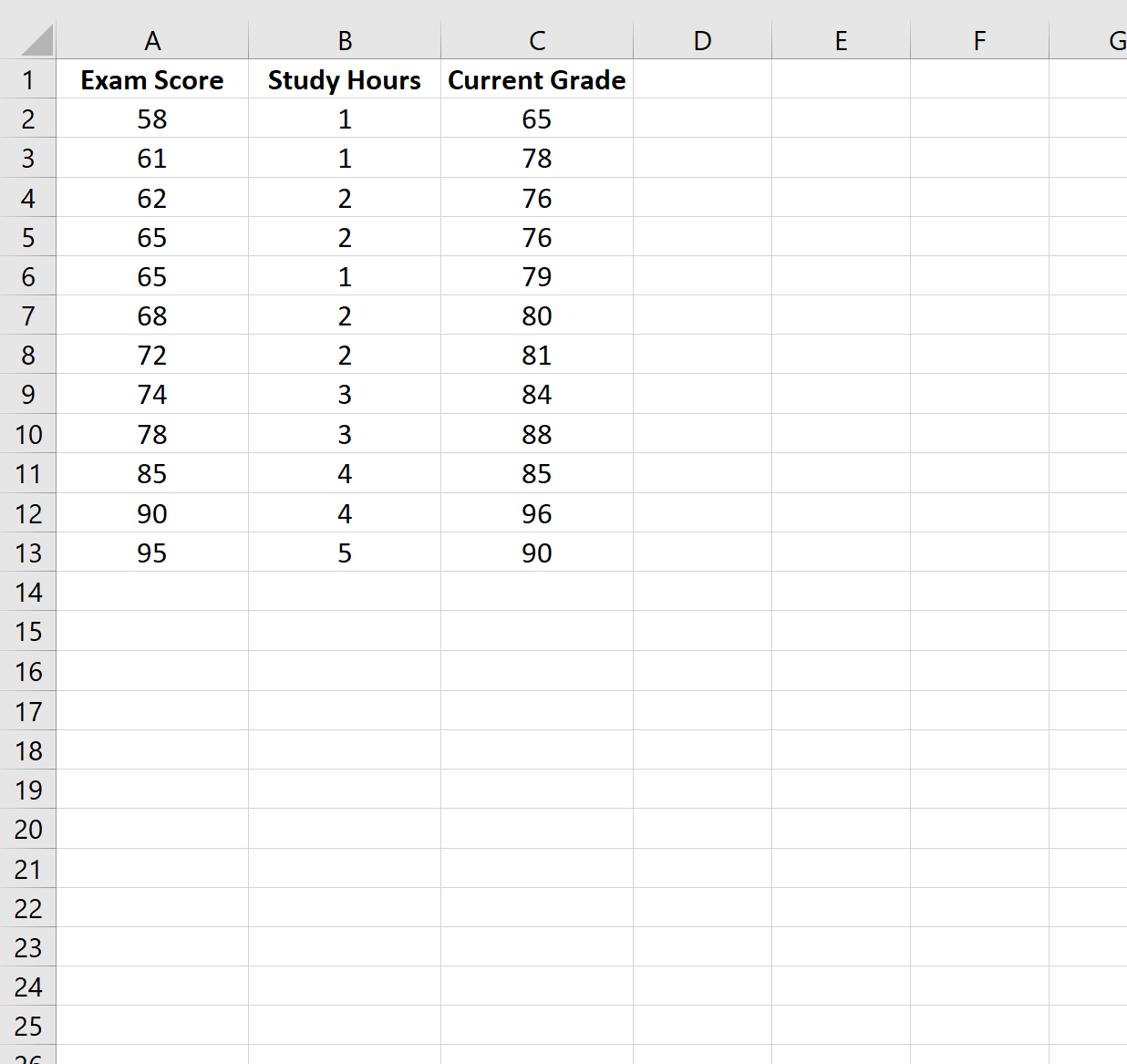
В этом примере мы создадим набор данных, содержащий следующие переменные для 12 разных студентов:
- Результаты экзамена
- Часы, потраченные на учебу
- Текущий класс
Шаг 2. Подберите регрессионную модель
Далее мы подберем модель множественной линейной регрессии , используя оценку на экзамене в качестве переменной ответа , а часы обучения и текущую оценку в качестве предикторных переменных.
Для этого щелкните вкладку «Данные» на верхней ленте, затем нажмите «Анализ данных »:

Если эта опция недоступна, необходимо сначала загрузить Data Analysis ToolPak .
В появившемся окне выберите Регрессия . В появившемся новом окне укажите следующую информацию:
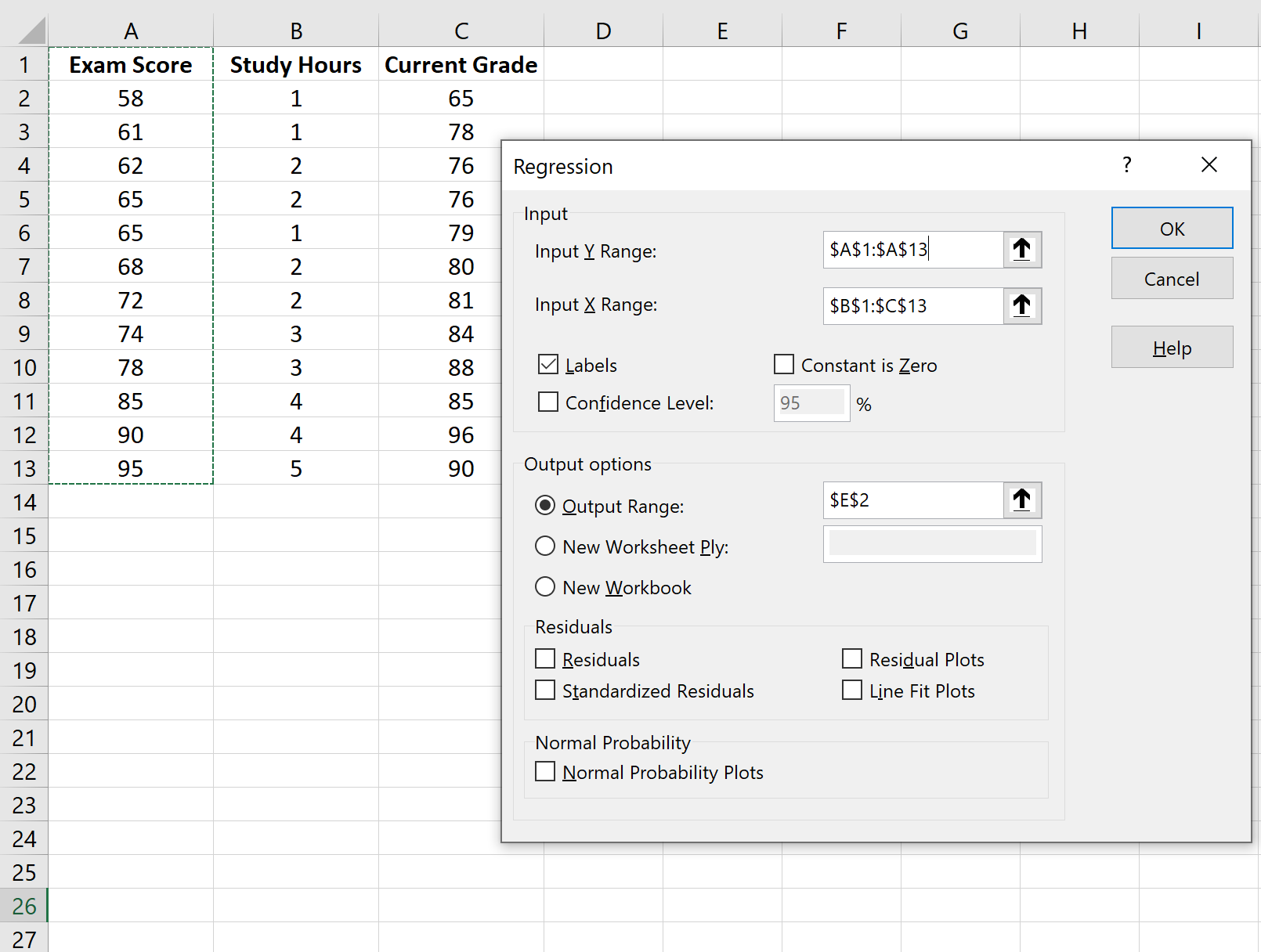
Как только вы нажмете «ОК» , появятся выходные данные регрессионной модели:
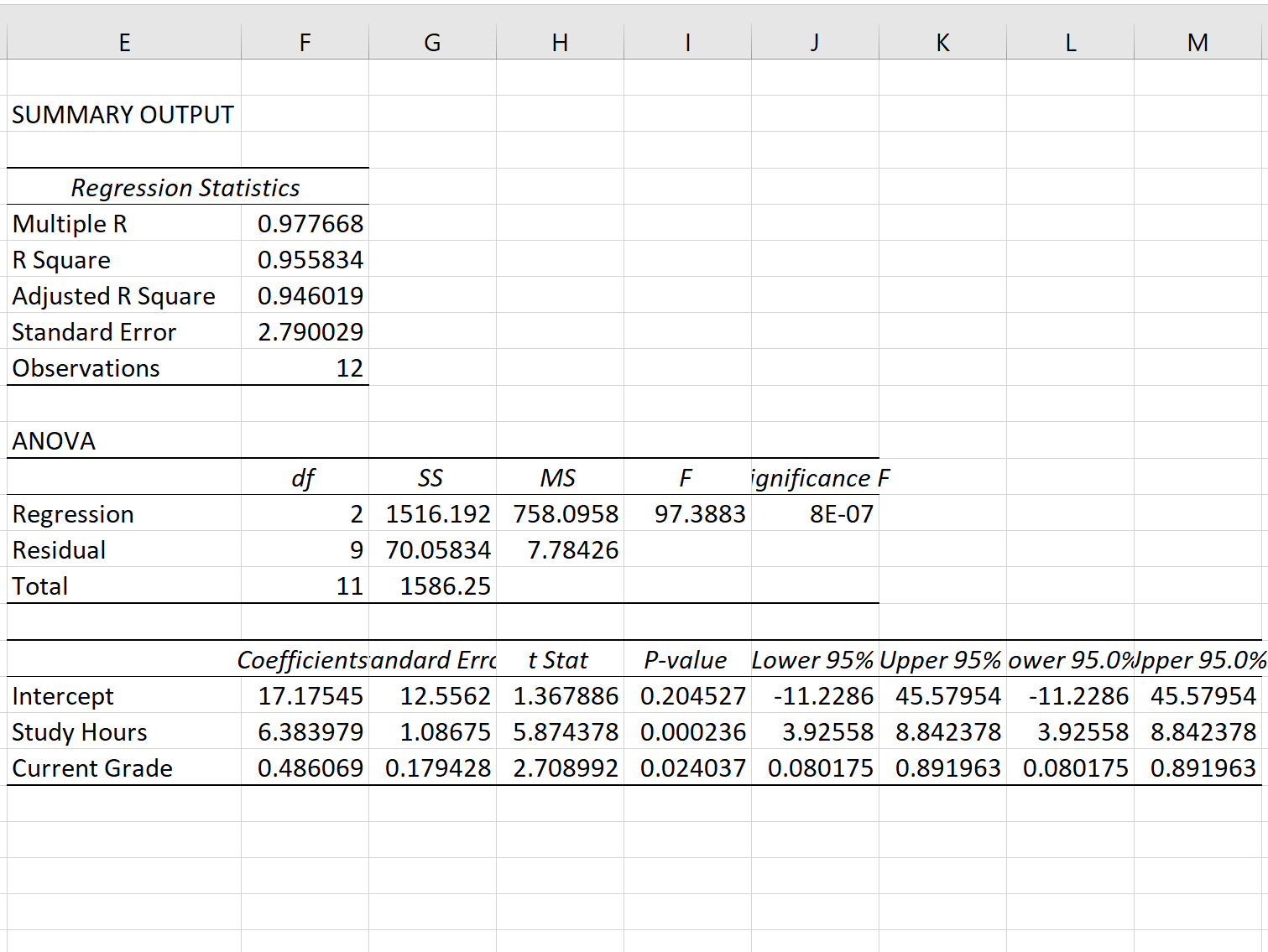
Шаг 3. Интерпретация стандартной ошибки регрессии
Стандартная ошибка регрессионной модели — это число рядом со стандартной ошибкой :
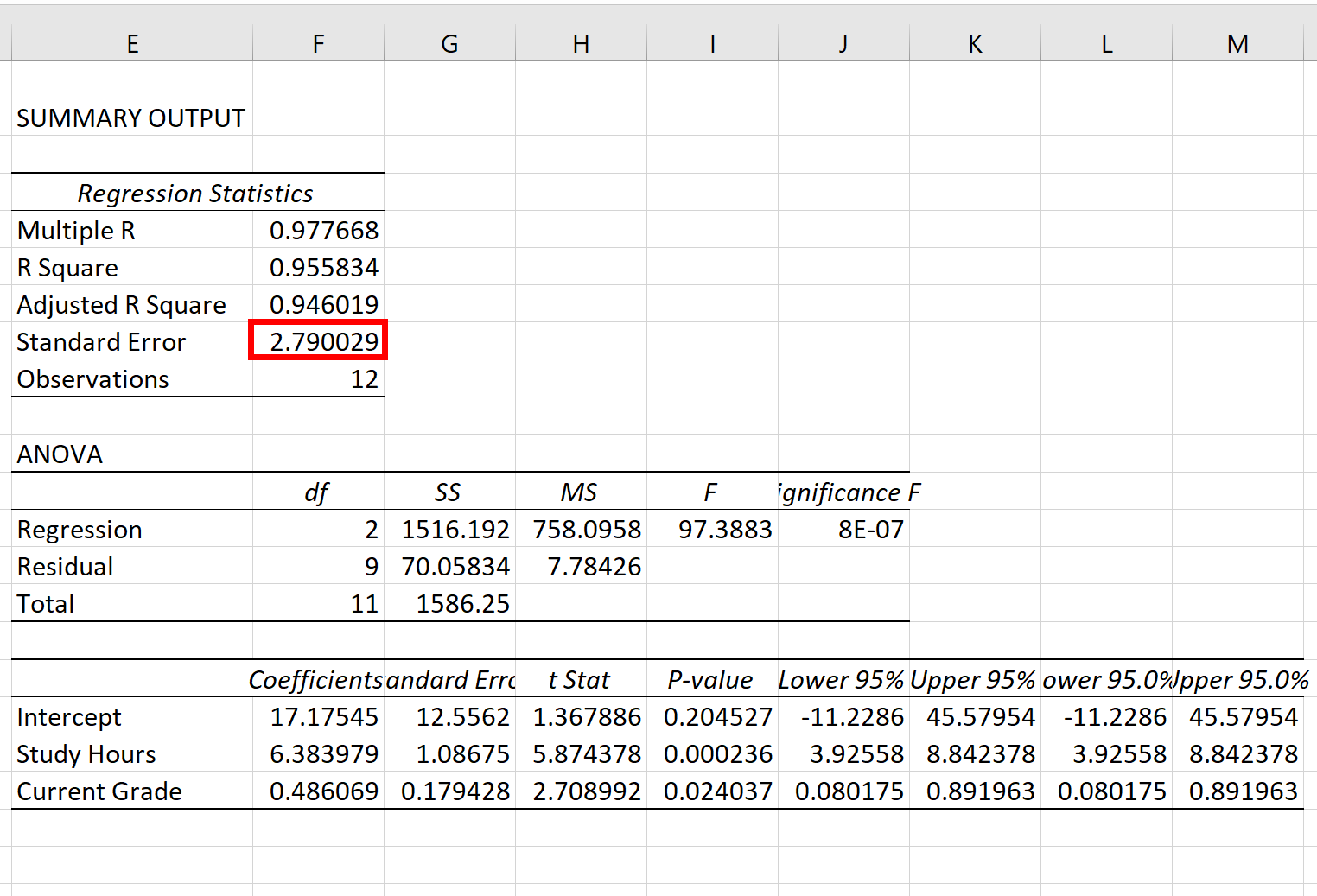
Стандартная ошибка этой конкретной регрессионной модели равна 2,790029 .
Это число представляет собой среднее расстояние между фактическими результатами экзамена и результатами экзамена, предсказанными моделью.
Обратите внимание, что результаты некоторых экзаменов будут отличаться от прогнозируемого балла более чем на 2,79 единицы, а другие — ближе. Но в среднем расстояние между фактическими результатами экзамена и прогнозируемыми результатами составляет 2,790029 .
Также обратите внимание, что меньшая стандартная ошибка регрессии указывает на то, что модель регрессии более точно соответствует набору данных.
Итак, если мы адаптируем новую модель регрессии к набору данных и получим стандартную ошибку, скажем, 4,53 , эта новая модель будет менее эффективна для прогнозирования результатов экзамена, чем предыдущая модель.
Дополнительные ресурсы
Другой распространенный способ измерения точности регрессионной модели — использование R-квадрата. Прочтите эту статью , чтобы получить хорошее объяснение преимуществ использования стандартной ошибки регрессии для измерения точности по сравнению с R-квадратом.