Стандартное отклонение и стандартная ошибка: в чем разница?

Два термина, которые студенты часто путают в статистике, — это стандартное отклонение и стандартная ошибка .

Стандартное отклонение измеряет распределение значений в наборе данных.

Стандартная ошибка — это стандартное отклонение среднего значения повторных выборок из популяции.

Давайте рассмотрим пример, чтобы наглядно проиллюстрировать эту идею.

Пример: стандартное отклонение по сравнению со стандартной ошибкой.

Предположим, мы измеряем вес 10 разных черепах.

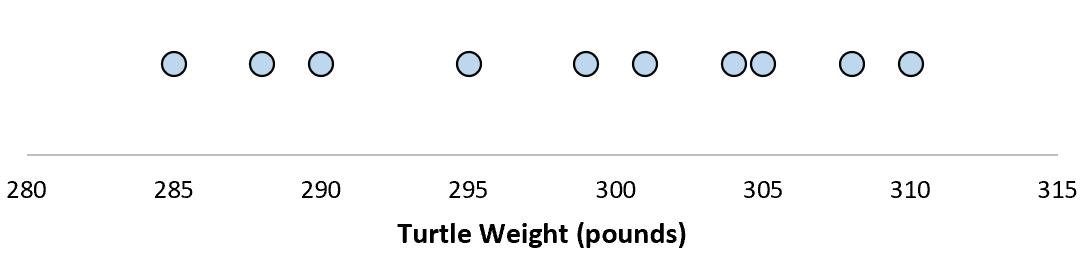
Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:

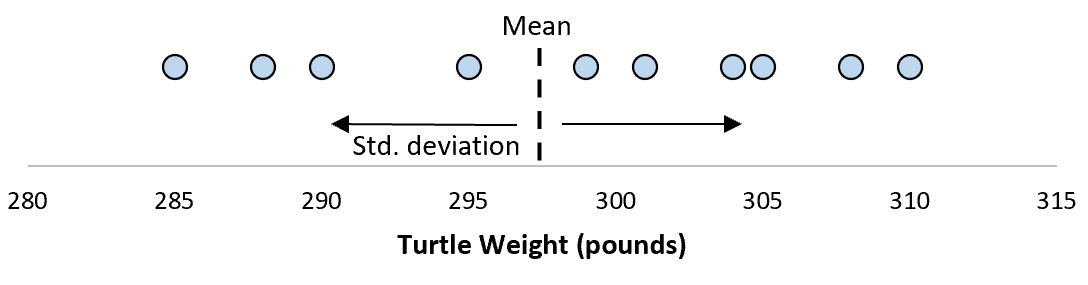
Предположим, что стандартное отклонение равно 8,68. Это дает нам представление о распределении веса этих черепах.

Но предположим, что мы соберем еще одну простую случайную выборку из 10 черепах и также проведем их измерения.

Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они происходят из одной и той же популяции:

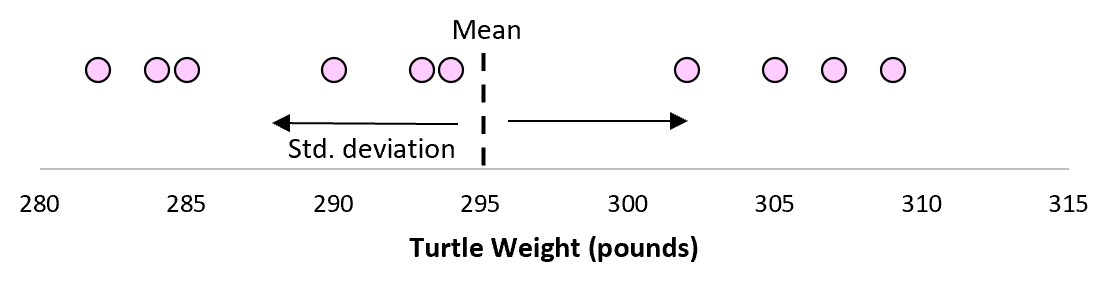
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем среднее значение выборки и стандартное отклонение выборки для каждой выборки:

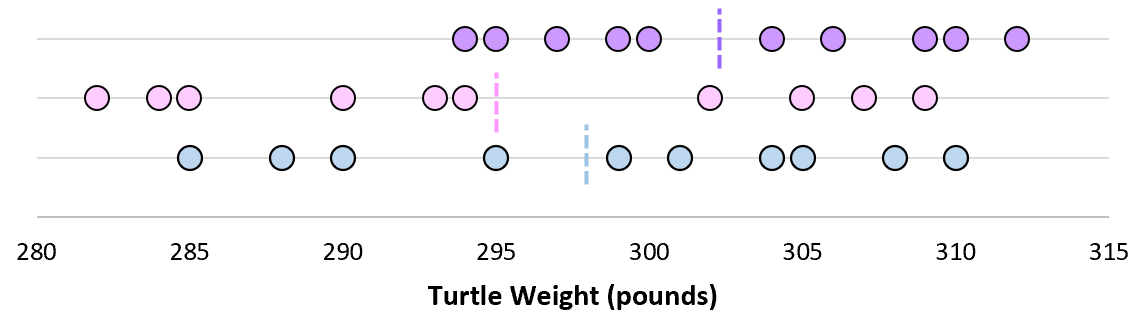
Теперь представьте, что мы наносим каждое из выборочных средних значений на одну и ту же строку:

Стандартное отклонение этих средних называется стандартной ошибкой.

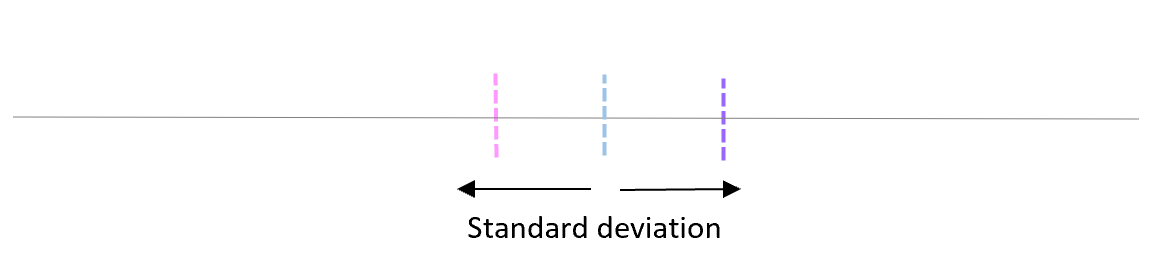
Формула для фактического расчета стандартной ошибки:

Стандартная ошибка = s/ √ n

Золото:

• s: выборочное стандартное отклонение
• n: размер выборки

Какой смысл использовать стандартную ошибку?

Когда мы вычисляем среднее значение данной выборки, мы на самом деле не хотим знать среднее значение этой конкретной выборки, а скорее среднее значение более крупной совокупности, из которой взята выборка.

Однако мы используем выборки, потому что по ним гораздо проще собрать данные, чем по всей совокупности.

И, конечно же, выборочное среднее варьируется от выборки к выборке, поэтому мы используем стандартную ошибку среднего как способ измерения точности нашей оценки среднего.

В формуле расчета стандартной ошибки вы заметите, что с увеличением размера выборки (n) стандартная ошибка уменьшается:

Стандартная ошибка = s/ √ n

Это должно иметь смысл, поскольку более крупные выборки уменьшают изменчивость и увеличивают вероятность того, что наше выборочное среднее будет ближе к истинному генеральному среднему значению.

Когда использовать стандартное отклонение или стандартную ошибку

Если мы просто хотим измерить распределение значений в наборе данных, мы можем использовать стандартное отклонение .

Однако, если мы хотим количественно оценить неопределенность вокруг оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .

В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать стандартное отклонение или стандартную ошибку.