Как проверить мультиколлинеарность в stata
Мультиколлинеарность в регрессионном анализе возникает, когда две или более объясняющих переменных сильно коррелируют друг с другом, так что они не предоставляют уникальную или независимую информацию в регрессионной модели. Если степень корреляции между переменными достаточно высока, это может вызвать проблемы при подборе и интерпретации регрессионной модели.
Например, предположим, что вы запускаете множественную линейную регрессию со следующими переменными:
Переменная реакция: максимальный вертикальный прыжок
Независимые переменные: размер обуви, рост, время, потраченное на тренировку.
В этом случае объясняющие переменные размер обуви и рост, вероятно, сильно коррелируют, поскольку высокие люди, как правило, имеют обувь большего размера. Это означает, что мультиколлинеарность, вероятно, будет проблемой в этой регрессии.
К счастью, можно обнаружить мультиколлинеарность с помощью показателя, называемого коэффициентом инфляции дисперсии (VIF) , который измеряет корреляцию и силу корреляции между объясняющими переменными в регрессионной модели.
В этом руководстве объясняется, как использовать VIF для обнаружения мультиколлинеарности в регрессионном анализе в Stata.
Пример: мультиколлинеарность в Stata
В этом примере мы будем использовать встроенный набор данных Stata под названием auto . Используйте следующую команду для загрузки набора данных:
использовать автоматически
Мы будем использовать команду регресса , чтобы подогнать модель множественной линейной регрессии, используя цену в качестве переменной ответа, а вес, длину и мили на галлон в качестве объясняющих переменных:
регрессия цена вес длина миль на галлон
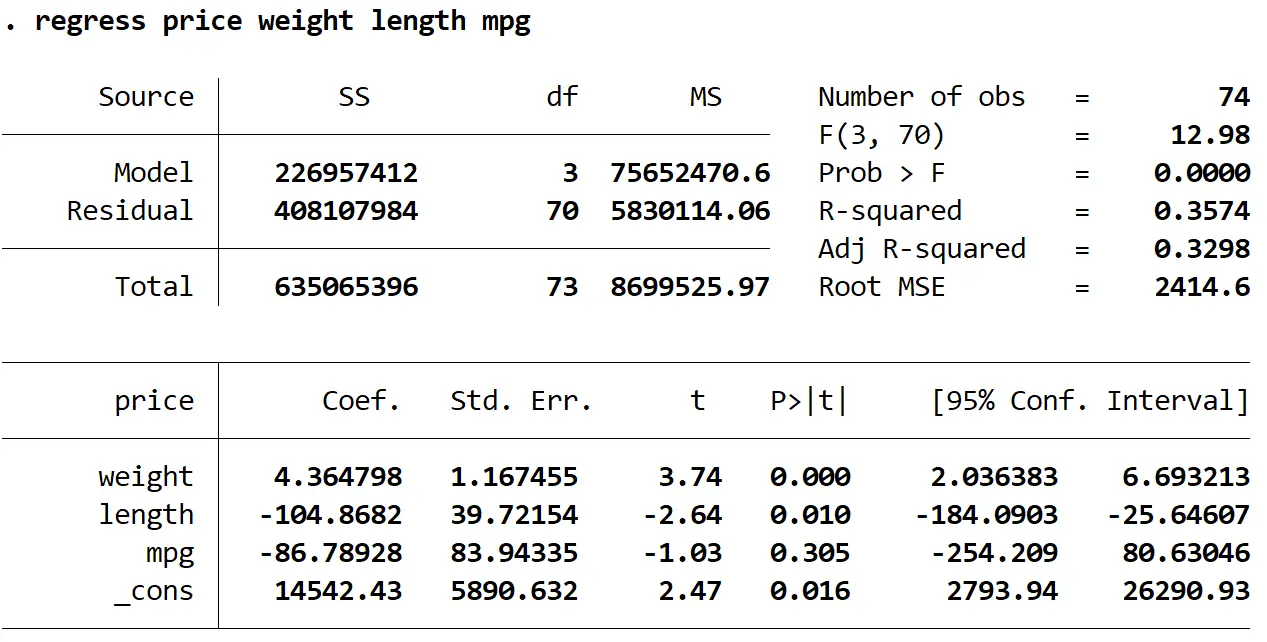
Далее мы будем использовать команду vive для проверки мультиколлинеарности:
оживленный
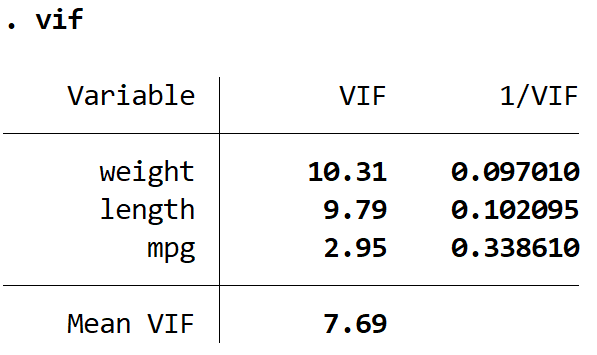
В результате получается значение VIF для каждой объясняющей переменной модели. Значение VIF начинается с 1 и не имеет верхнего предела. Общее правило интерпретации VIF следующее:
- Значение 1 указывает на отсутствие корреляции между данной объясняющей переменной и любой другой объясняющей переменной в модели.
- Значение от 1 до 5 указывает на умеренную корреляцию между данной объясняющей переменной и другими объясняющими переменными в модели, но часто она недостаточно серьезна, чтобы требовать особого внимания.
- Значение больше 5 указывает на потенциально серьезную корреляцию между данной независимой переменной и другими объясняющими переменными в модели. В этом случае оценки коэффициентов и значения p в результатах регрессии, скорее всего, ненадежны.
Мы видим, что значения VIF для веса и длины больше 5, что указывает на то, что мультиколлинеарность, вероятно, является проблемой в регрессионной модели.
Как бороться с мультиколлинеарностью
Часто самый простой способ справиться с мультиколлинеарностью — просто удалить одну из проблемных переменных, поскольку удаляемая переменная в любом случае, вероятно, является избыточной и добавляет в модель мало уникальной или независимой информации.
Чтобы определить, какую переменную удалить, мы можем использовать команду corr для создания матрицы корреляции для отображения коэффициентов корреляции между каждой из переменных в модели. Это может помочь нам определить, какие переменные могут быть сильно коррелированы друг с другом и могут вызвать проблема мультиколлинеарности:
цена, вес, длина, мили на галлон
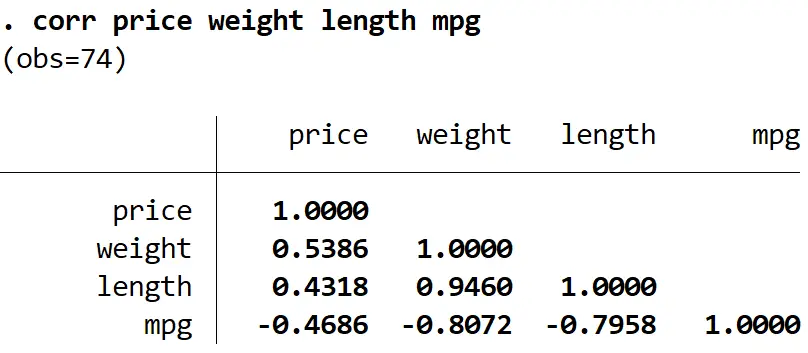
Мы видим, что длина сильно коррелирует как с весом, так и с расходом миль на галлон, и имеет наименьшую корреляцию с ценой переменной ответа. Таким образом, удаление длины модели может решить проблему мультиколлинеарности без снижения общего качества регрессионной модели.
Чтобы проверить это, мы можем снова запустить регрессионный анализ, используя только вес и мили на галлон в качестве объясняющих переменных:
регрессия цена вес миль на галлон
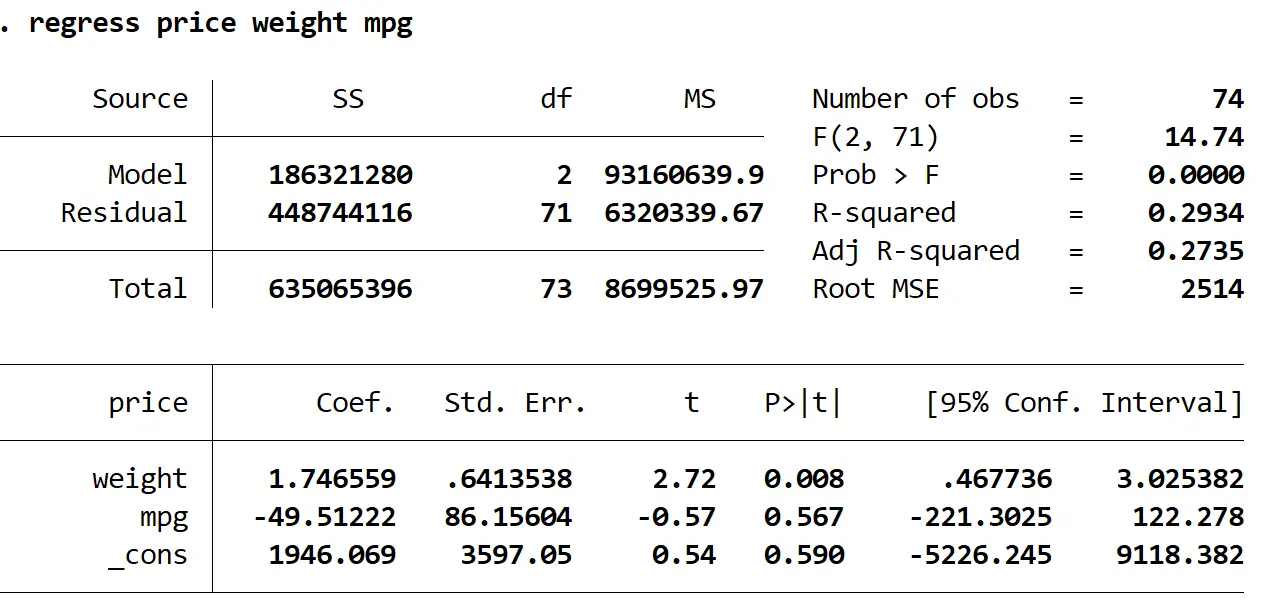
Мы видим, что скорректированный R-квадрат этой модели составляет 0,2735 по сравнению с 0,3298 в предыдущей модели. Это указывает на то, что общая полезность модели лишь незначительно снизилась. Затем мы можем найти значения VIF с помощью команды VIF :
ОЖИВЛЕННЫЙ
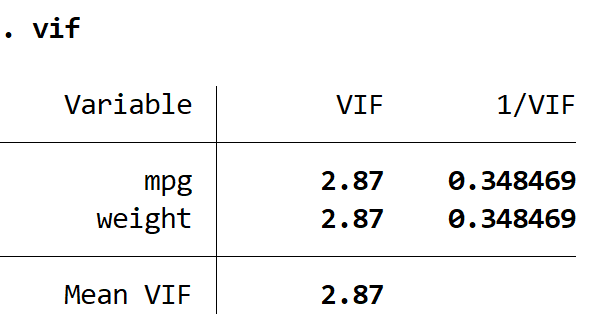
Оба значения VIF меньше 5, что указывает на то, что мультиколлинеарность больше не является проблемой в модели.