Как проверить нормальность в stata
Многие статистические тесты требуют, чтобы одна или несколько переменных были нормально распределены , чтобы результаты тестов были надежными.
В этом руководстве объясняется несколько методов, которые можно использовать для проверки нормальности переменных в Stata.
Для каждого из этих методов мы будем использовать встроенный набор данных Stata под названием auto . Вы можете загрузить этот набор данных с помощью следующей команды:
автоматическое использование системы
Способ 1: гистограммы
Неофициальный способ проверить, нормально ли распределена переменная, — создать гистограмму , отображающую распределение переменной.
Если переменная нормально распределена, гистограмма должна принять форму «колокольчика» с большим количеством значений, расположенным вблизи центра, и меньшим количеством значений, расположенных на хвостах.
Мы можем использовать команду hist для создания гистограммы для переменной смещения :
движущаяся история
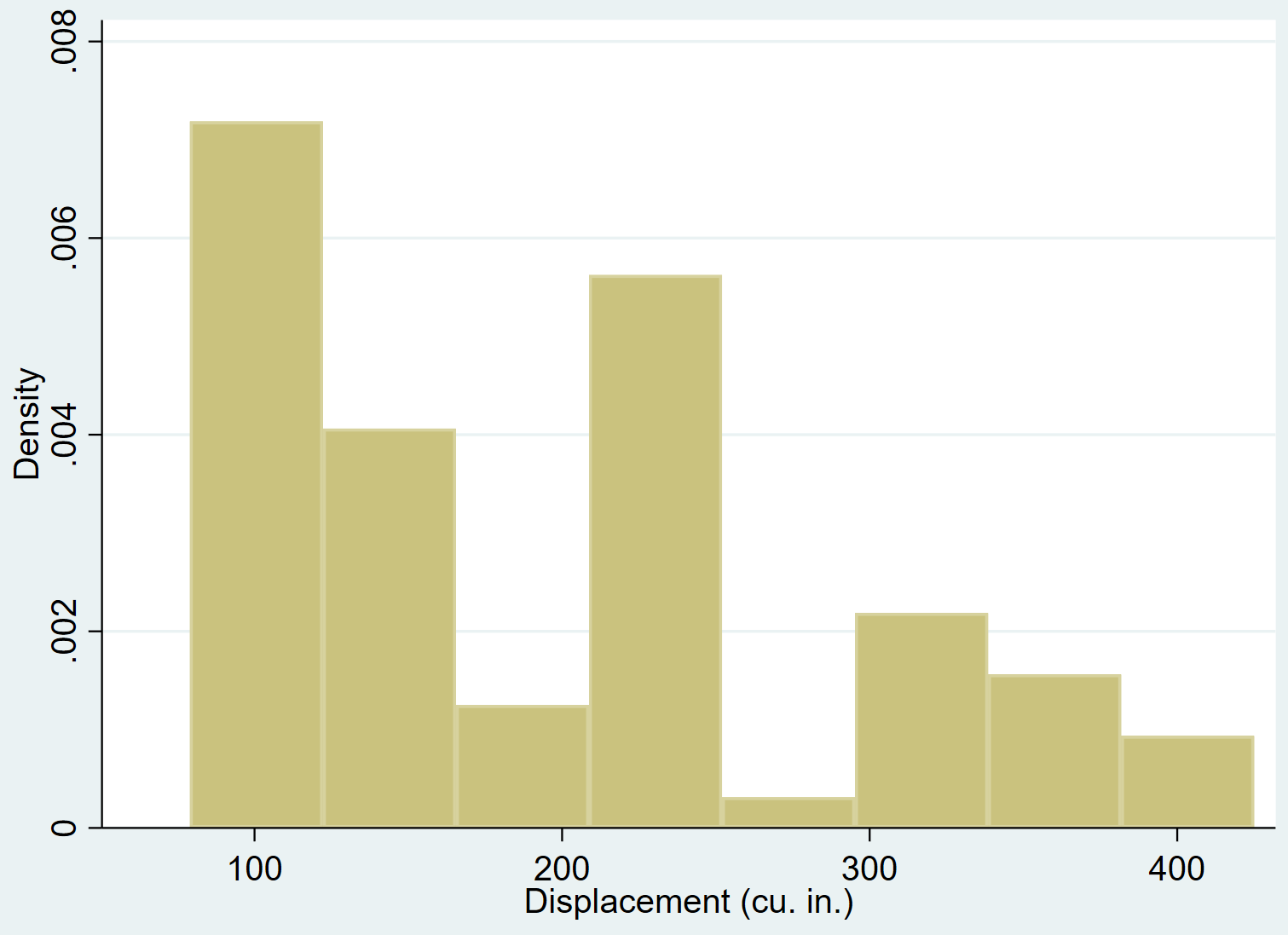
Мы можем добавить кривую нормальной плотности к гистограмме с помощью нормальной команды:
движущаяся история, нормальная
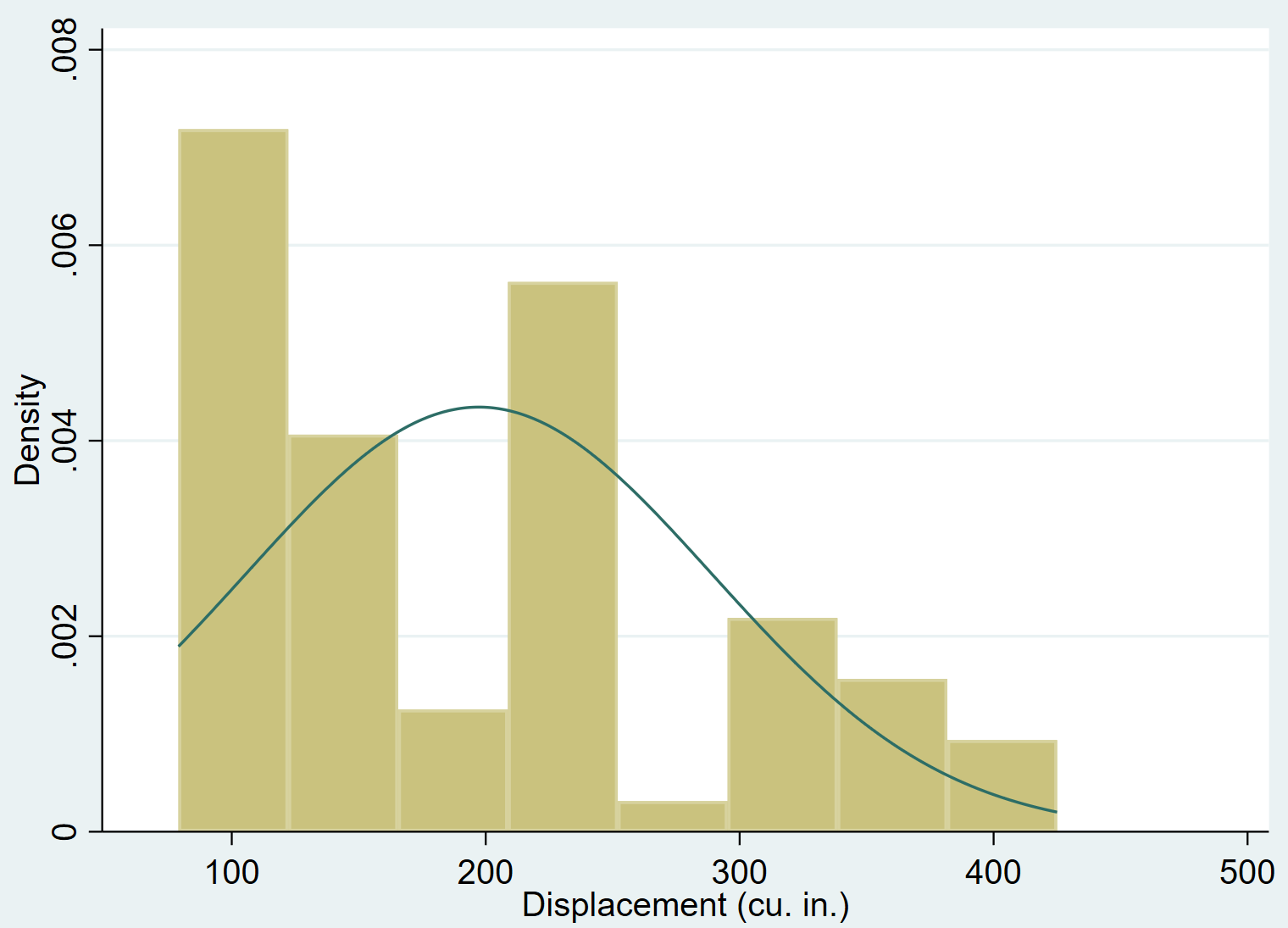
Совершенно очевидно, что сдвиг переменной смещен вправо (например, большинство значений сосредоточено слева, а длинный «хвост» значений простирается вправо) и не соответствует нормальному распределению.
Связанный: Левое и правое асимметричное распределение
Метод 2: тест Шапиро-Уилка.
Формальным способом проверки нормальности является использование теста Шапиро-Уилка .
Нулевая гипотеза для этого теста состоит в том, что переменная имеет нормальное распределение. Если значение p теста ниже определенного уровня значимости (обычные варианты включают 0,01, 0,05 и 0,10), то мы можем отвергнуть нулевую гипотезу и сделать вывод, что имеется достаточно доказательств, чтобы утверждать, что переменная не имеет нормального распределения. .
*Этот тест можно использовать, когда общее количество наблюдений составляет от 4 до 2000.
Мы можем использовать команду swilk для выполнения теста Шапиро-Уилка на переменном смещении :
плавное движение

Вот как интерпретировать результат теста:
Набл.: 74. Это количество наблюдений, использованных в тесте.
Вт: 0,92542. Это тестовая статистика для теста.
Вероятность>z: 0,00031. Это значение p, связанное со статистикой теста.
Поскольку значение p меньше 0,05, мы можем отвергнуть нулевую гипотезу теста. У нас есть достаточно доказательств, чтобы сказать, что переменное смещение не имеет нормального распределения.
Мы также можем выполнить тест Шапиро-Уилка для нескольких переменных одновременно, указав несколько переменных после команды swilk :
объем Swilk, длина миль на галлон
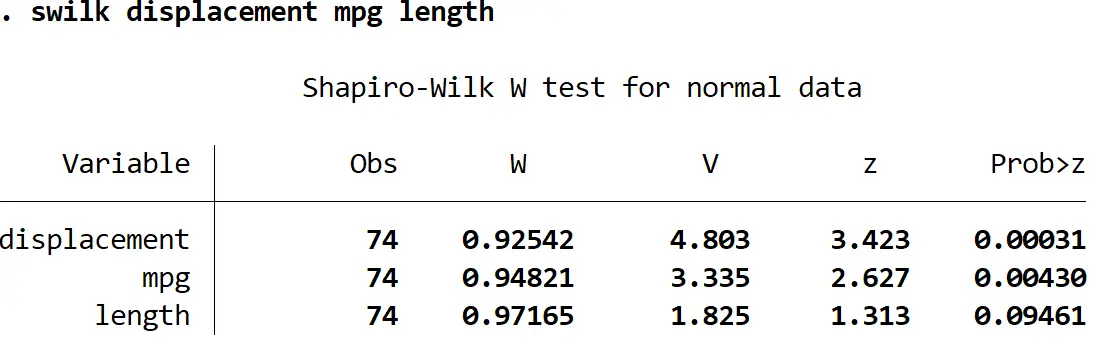
Используя уровень значимости 0,05, мы бы пришли к выводу, что объем двигателя и мили на галлон не имеют нормального распределения, но у нас нет достаточных доказательств, чтобы сказать, что длина не имеет нормального распределения.
Метод 3: тест Шапиро-Франсия
Другой формальный способ проверить нормальность — использовать тест Шапиро-Франсиа .
Нулевая гипотеза для этого теста состоит в том, что переменная имеет нормальное распределение. Если p-значение теста ниже определенного уровня значимости, то мы можем отвергнуть нулевую гипотезу и заключить, что имеется достаточно доказательств того, что переменная не имеет нормального распределения.
*Этот тест можно использовать, когда общее количество наблюдений составляет от 10 до 5000.
Мы можем использовать команду sfrancia для выполнения теста Шапиро-Уилка на переменном смещении :
переезд Сфранция

Вот как интерпретировать результат теста:
Набл.: 74. Это количество наблюдений, использованных в тесте.
W’: 0,93011. Это тестовая статистика для теста.
Вероятность>z: 0,00094. Это значение p, связанное со статистикой теста.
Поскольку значение p меньше 0,05, мы можем отвергнуть нулевую гипотезу теста. У нас есть достаточно доказательств, чтобы сказать, что переменное смещение не имеет нормального распределения.
Подобно тесту Шапиро-Уилка, вы можете выполнить тест Шапиро-Франсиа для нескольких переменных одновременно, указав несколько переменных после команды sfrancia .
Метод 4: проверка асимметрии и эксцесса
Другой способ проверить нормальность — использовать тест асимметрии и эксцесса , который определяет, соответствуют ли асимметрия и эксцесс переменной нормальному распределению.
Нулевая гипотеза для этого теста состоит в том, что переменная имеет нормальное распределение. Если p-значение теста ниже определенного уровня значимости, то мы можем отвергнуть нулевую гипотезу и заключить, что имеется достаточно доказательств того, что переменная не имеет нормального распределения.
*Для этого теста требуется минимум 8 наблюдений.
Мы можем использовать команду sktest для проверки асимметрии и эксцесса переменной смещения :
перенос теста

Вот как интерпретировать результат теста:
Набл.: 74. Это количество наблюдений, использованных в тесте.
прил хи(2): 5.81. Это статистика теста хи-квадрат для теста.
Вероятность>chi2: 0,0547. Это значение p, связанное со статистикой теста.
Поскольку значение p не меньше 0,05, мы не можем отвергнуть нулевую гипотезу теста. У нас недостаточно доказательств, чтобы сказать, что движения обычно не распределяются.
Подобно другим тестам на нормальность, вы можете выполнить тест на асимметрию и эксцесс сразу для нескольких переменных, указав несколько переменных после команды sktest .