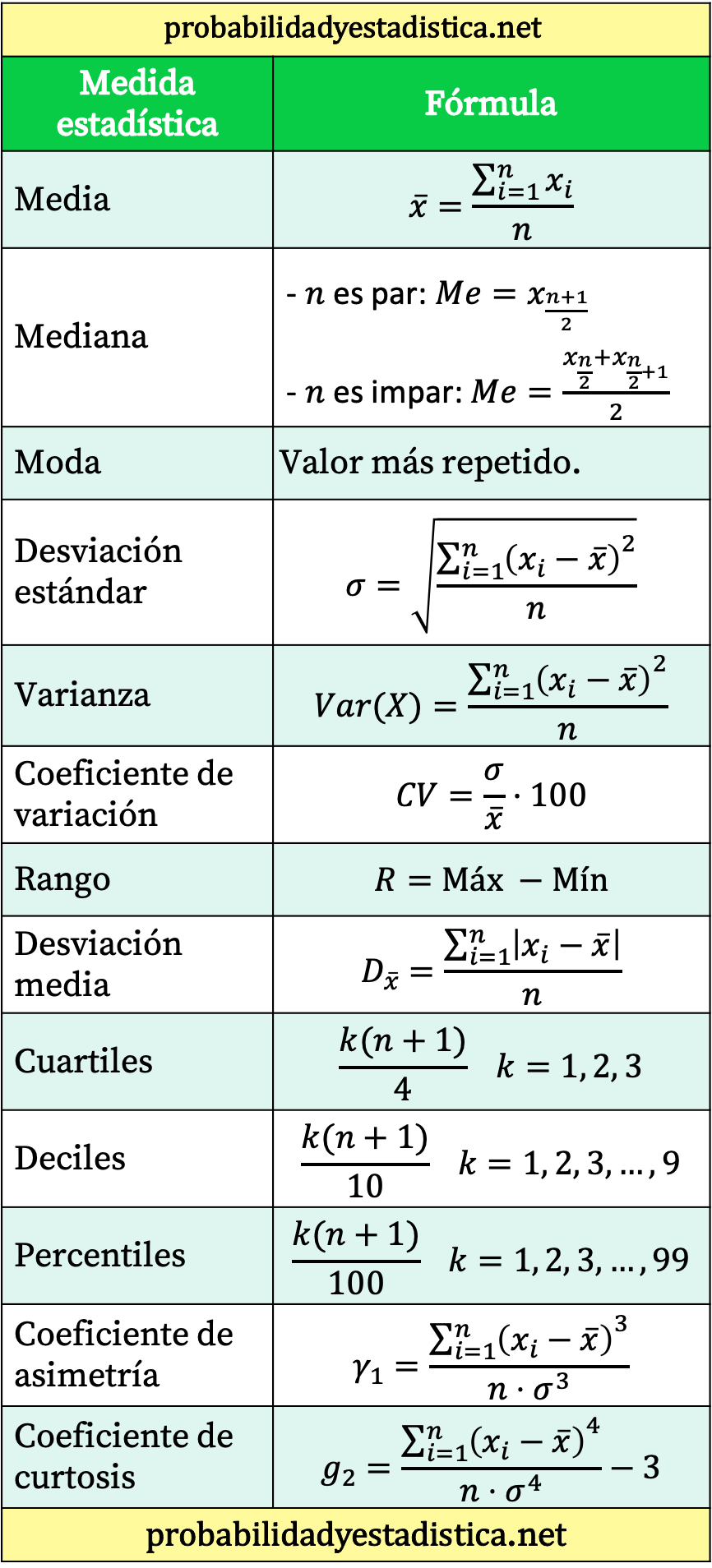
Статистические формулы

К бенджамин андерсон 1 августа, 2023 Статистика 0 комментариев

Здесь вы найдете основные статистические формулы. Мы также оставляем вам ссылку на наши статьи, в которых вы можете увидеть примеры применения каждой статистической формулы и, кроме того, вы можете воспользоваться онлайн-калькулятором, чтобы не выполнять расчеты и узнать результат формулы напрямую.

Формулы для статистических показателей центральной тенденции

Половина

Чтобы вычислить среднее значение, сложите все значения, а затем разделите их на общее количество данных. Таким образом, формула среднего значения выглядит следующим образом:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}$

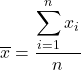
В статистике среднее значение также известно как среднее арифметическое или среднее .

➤ См. « Калькулятор среднего арифметического».

медиана

Медиана — это среднее значение всех данных, упорядоченных от наименьшего к наибольшему. Другими словами, медиана делит упорядоченный набор данных на две равные части.

Расчет медианы зависит от того, является ли общее количество данных четным или нечетным:

Если общее количество данных нечетное , медианой будет значение, попадающее прямо в середину данных. То есть значение, которое находится в позиции (n+1)/2 отсортированных данных.

$Me=x_{\frac{n+1}{2}$

Если общее количество точек данных четное , медиана будет средним значением двух точек данных, расположенных в центре. То есть среднее арифметическое значений, которые находятся в позициях n/2 и n/2+1 упорядоченных данных.

$Me=\cfrac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}$

Золото

$n$

— общее количество данных в выборке, а символ Me обозначает медиану.

➤ См.: Калькулятор медианы

Мода

В статистике мода — это значение в наборе данных, имеющее наибольшую абсолютную частоту, то есть мода — это наиболее повторяющееся значение в наборе данных.

Таким образом, не существует конкретной формулы для режима, но для расчета режима набора статистических данных просто подсчитайте, сколько раз каждый элемент данных появляется в выборке, и наиболее повторяющиеся данные будут режимом.

Этот режим также можно назвать статистическим режимом или модальным значением .

➤ См.: Калькулятор моды.

Формулы статистических мер дисперсии

Среднеквадратичное отклонение

Стандартное отклонение, также называемое стандартным отклонением, равно квадратному корню из суммы квадратов отклонений ряда данных, разделенной на общее количество наблюдений.

Следовательно, формула стандартного отклонения имеет вид:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n}}$

➤ См.: Калькулятор стандартного отклонения.

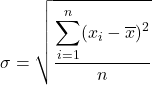
Дисперсия

Дисперсия равна сумме квадратов остатков по общему числу наблюдений. Таким образом, формула для этого статистического показателя выглядит следующим образом:

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}$

Золото:

$X$

— случайная величина, для которой вы хотите вычислить дисперсию.
$x_i$

значение данных

$i$

.
$n$

общее количество наблюдений.
$\overline{X}$

среднее значение случайной величины

$X$

.

➤ См.: Калькулятор зазора.

Коэффициент вариации

В статистике коэффициент вариации — это мера дисперсии, используемая для определения дисперсии набора данных относительно его среднего значения. Коэффициент вариации рассчитывается путем деления стандартного отклонения данных на их среднее значение, а затем умножения на 100, чтобы выразить значение в процентах.

$CV=\cfrac{\sigma}{\overline{x}}\cdot 100$

➤ См.: Калькулятор коэффициента вариации.

Аккуратный

Статистический диапазон — это мера дисперсии, которая указывает на разницу между максимальным и минимальным значением данных в выборке. Следовательно, чтобы рассчитать размер генеральной совокупности или статистической выборки, максимальное значение необходимо вычесть из минимального значения.

$R=\text{M\'ax}-\text{M\'in}$

➤ См.: Пример статистического диапазона.

Межквартильный размах

Межквартильный размах , также называемый межквартильным размахом , является мерой статистической дисперсии, которая указывает на разницу между третьим и первым квартилем.

Следовательно, чтобы вычислить межквартильный размах набора статистических данных, необходимо сначала найти третий и первый квартиль, а затем вычесть их.

$IQR=Q_3-Q_1$

➤ См.: Калькулятор межквартильного размаха.

средняя разница

Среднее отклонение , также называемое средним абсолютным отклонением , представляет собой среднее значение абсолютных отклонений. Таким образом, среднее отклонение равно сумме отклонений каждого элемента данных от среднего арифметического, деленной на общее количество элементов данных.

$D_{\overline{x}}=\cfrac{\sum_{i=1}^n|x_i-\overline{x}|}{n}$

➤ См.: Калькулятор среднего отклонения.

Формулы для статистических измерений положения

квартили

В статистике квартили — это три значения, которые делят набор упорядоченных данных на четыре равные части. Таким образом, первый, второй и третий квартили представляют соответственно 25%, 50% и 75% всех статистических данных.

Квартили обозначаются заглавной буквой Q и индексом квартиля, поэтому первый квартиль — это Q ₁ , второй квартиль — Q ₂ и третий квартиль — Q ₃ .

Формула квартиля :

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Обратите внимание: эта формула сообщает нам положение квартиля, а не его значение. Квартилем будут данные, расположенные в позиции, полученной по формуле.

Однако иногда результат этой формулы даст нам десятичное число. Поэтому мы должны различать два случая в зависимости от того, является ли результат десятичным числом или нет:

Если результатом формулы является число без десятичной части , квартилем являются данные, находящиеся в позиции, указанной в формуле выше.
Если результатом формулы является число с десятичной частью , значение квартиля рассчитывается по следующей формуле:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

Где x _i и x _i+1 — номера позиций, между которыми находится число, полученное по первой формуле, а d — десятичная часть числа, полученного по первой формуле.

➤ См.: Калькулятор квартилей.

децили

В статистике децили — это девять величин, которые делят набор упорядоченных данных на десять равных частей. Таким образом, первый, второй, третий… дециль представляет 10%, 20%, 30%… выборки или совокупности.

Децили обозначаются заглавной буквой Д и децильным индексом, то есть первый дециль — Д ₁ , второй дециль — Д ₂ , третий дециль — Д ₃ и т. д.

Децильная формула выглядит следующим образом:

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,4,5,6,7,8,9$

Обратите внимание: эта формула сообщает нам положение дециля, а не его значение. Децилем будут данные, расположенные в позиции, полученной по формуле.

Однако иногда результат этой формулы дает нам десятичное число, поэтому мы должны различать два случая в зависимости от того, является ли результат десятичным числом или нет:

Если результатом формулы является число без десятичной части , децилем являются данные, расположенные в позиции, указанной в формуле выше.
Если результатом формулы является число с десятичной частью , значение дециля рассчитывается по следующей формуле:

$D=x_i+d\cdot (x_{i+1}-x_i)$

➤ См.: Калькулятор децилей.

процентили

В статистике процентили — это значения, делящие набор упорядоченных данных на сто равных частей. Итак, процентиль указывает значение, ниже которого падает процент набора данных.

Процентили обозначаются заглавной буквой P и индексом процентиля, то есть первый процентиль — P ₁ , 40-й процентиль — P ₄₀ , 79-й процентиль — P ₇₉ и т. д.

Формула процентиля :

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Обратите внимание: эта формула сообщает нам положение процентиля, но не его значение. Процентилем будут данные, расположенные в позиции, полученной по формуле.

Если результатом формулы является число без десятичной части , процентиль соответствует данным, которые находятся в позиции, указанной формулой выше.
Если результатом формулы является число с десятичной частью , точное значение процентиля рассчитывается по следующей формуле:

$P=x_i+d\cdot (x_{i+1}-x_i)$

➤ См.: Калькулятор процентилей.

Статистические формулы измерения формы

коэффициент асимметрии

Коэффициент асимметрии или индекс асимметрии — это статистический коэффициент, используемый для определения асимметрии распределения. Итак, рассчитав коэффициент асимметрии, можно узнать тип асимметрии распределения без необходимости его графического представления.

Формула коэффициента асимметрии выглядит следующим образом:

$\displaystyle\gamma_1=\frac{\overline{x}_3}{\sigma^3}$

Аналогично, для расчета коэффициента асимметрии Фишера можно использовать любую из следующих двух формул:

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\overline{x}\right)^3}{n\cdot \sigma ^3}$

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\cdot \overline{x}\cdot \sigma^2 - \overline{x}^3}{\sigma^3}$

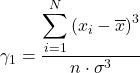
Золото

$E$

это математическое ожидание,

$\overline{x}$

среднее арифметическое,

$\sigma$

стандартное отклонение и

$n$

общее количество данных.

➤ См.: Коэффициент асимметрии.

коэффициент эксцесса

Куртозис, также называемый резкостью, показывает, насколько сконцентрировано распределение вокруг своего среднего значения. Другими словами, эксцесс показывает, является ли распределение крутым или пологим. В частности, чем больше эксцесс распределения, тем оно круче (или острее).

Формула коэффициента эксцесса выглядит следующим образом:

$\displaystyle g_2=\frac{1}{n}\cdot\frac{\displaystyle \sum_{i=1}^n(x_i-\overline{x})^4}{\sigma^4}-3$

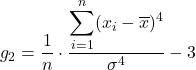
Золото

$x_i$

значение, соответствующее наблюдению

$i$

$\overline{x}$

среднее арифметическое,

$\sigma$

стандартное отклонение и

$n$

общее количество данных.

➤ См.: Калькулятор коэффициента сглаживания.

Сводная таблица всех статистических формул

Наконец, мы оставляем вам таблицу, в которой суммированы основные статистические формулы.

➤ См.: Формулы вероятности.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Формулы для статистических показателей центральной тенденции

Половина

медиана

Мода

Формулы статистических мер дисперсии

Среднеквадратичное отклонение

Дисперсия

Коэффициент вариации

Аккуратный

Межквартильный размах

средняя разница

Формулы для статистических измерений положения

квартили

децили

процентили

Статистические формулы измерения формы

коэффициент асимметрии

коэффициент эксцесса

Сводная таблица всех статистических формул

Об авторе

бенджамин андерсон

Добавить комментарий