Excel: создание статистического сравнения двух наборов данных

Часто вам может потребоваться выполнить статистическое сравнение двух наборов данных в Excel, чтобы понять, чем отличается распределение значений в каждом наборе данных.

Существует два распространенных способа выполнения статистического сравнения:

Метод 1. Рассчитайте пятизначную сводку каждого набора данных.

Мы можем рассчитать пятизначную сводку каждого набора данных, которая состоит из следующих значений:

• Минимальное значение
• Первый квартиль (25-й процентиль)
• Медиана (50-й процентиль)
• Третий квартиль (75-й процентиль)
• Максимум

Рассчитав эти пять значений, мы можем получить хорошее представление о распределении значений в каждом наборе данных.

Метод 2. Рассчитайте среднее и стандартное отклонение.

Более простой способ выполнить статистическое сравнение двух наборов данных — вычислить среднее и стандартное отклонение каждого набора данных.

Это помогает нам примерно понять, где находится «центральное» значение и каково распределение значений в каждом наборе данных.

В следующем примере показано, как использовать каждый из этих методов на практике.

Пример. Выполните статистическое сравнение двух наборов данных в Excel.

Предположим, у нас есть два набора данных в Excel, которые показывают результаты учащихся двух разных классов, полученные на конкретном экзамене:

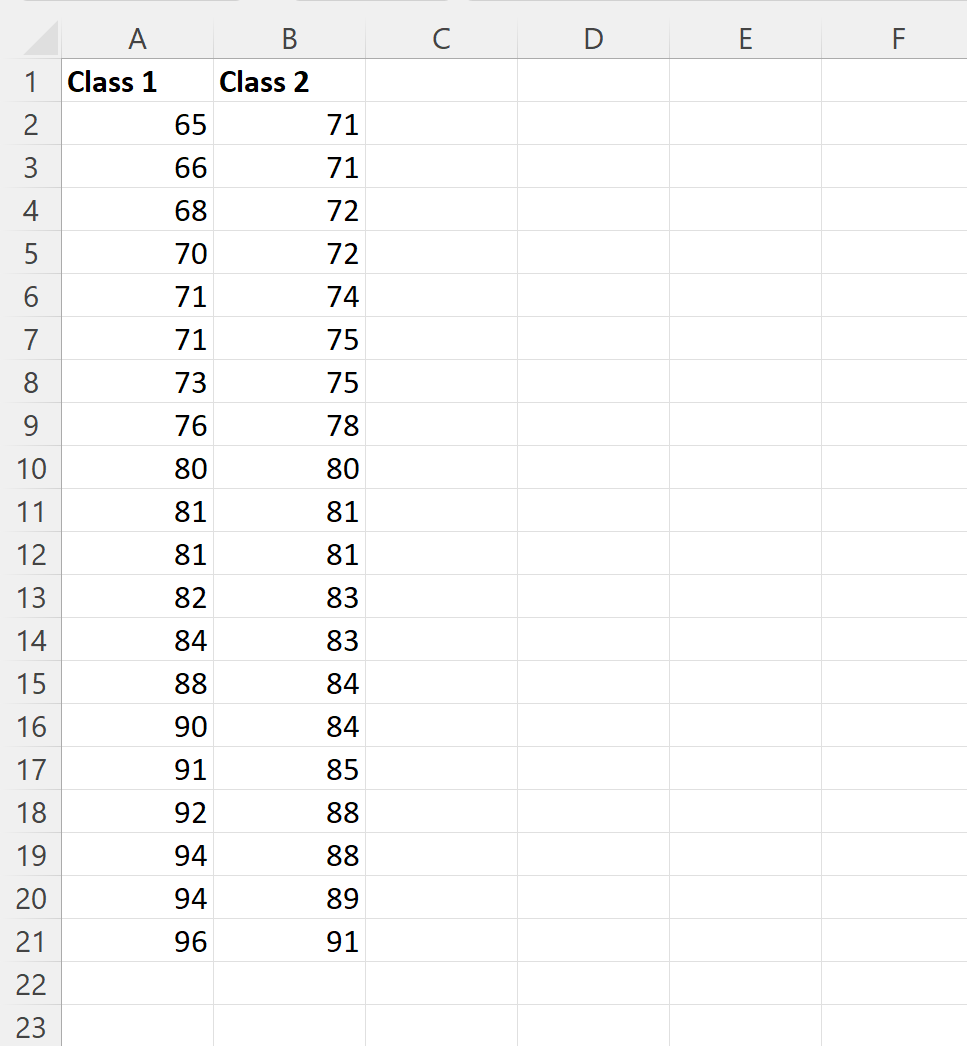
Мы можем ввести следующие формулы в ячейки столбца E, чтобы рассчитать пятизначную сводку результатов экзамена для 1 класса:

• E2 : =МИН(A2:A21)
• E3 : =КВАРТИЛЬ(A2:A21, 1)
• E4 : =МЕДИАНА(A2:A21)
• E5 : =КВАРТИЛЬ(A2:A21, 3)
• E6 : =MAX(A2:A21

Затем мы можем щелкнуть и перетащить эти формулы вправо, чтобы вычислить те же значения для класса 2:

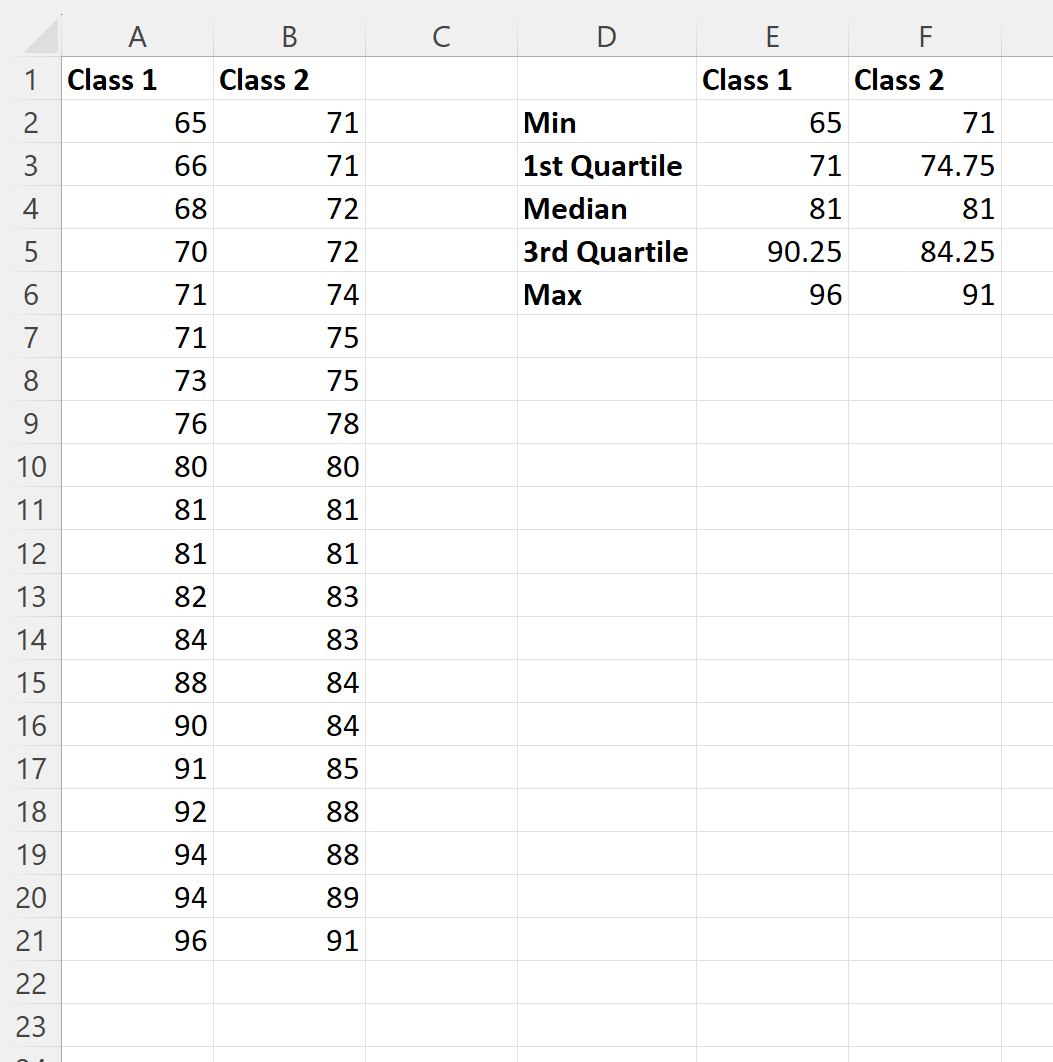
Затем мы можем ввести следующие формулы в ячейки столбца E, чтобы рассчитать среднее и стандартное отклонение результатов экзамена для класса 1:

• E8 : =СРЕДНЕЕ(A2:A21)
• E9 : =ETDEV(A2:A21, 1)

Затем мы можем щелкнуть и перетащить эти формулы вправо, чтобы вычислить те же значения для класса 2:

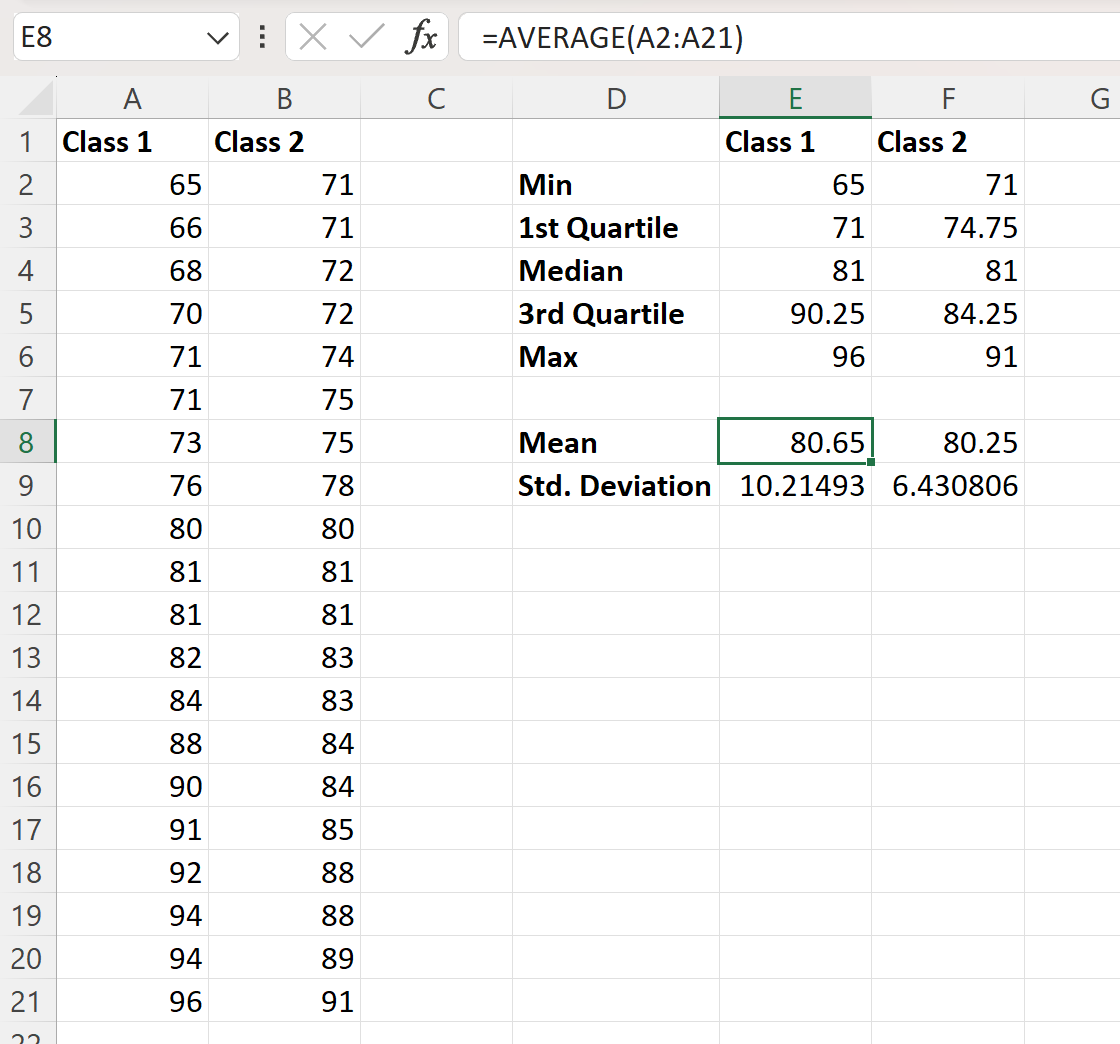
Из этого статистического сравнения двух наборов данных мы можем сделать следующие выводы:

Вывод 1: Оба набора данных имеют схожую «основную» ценность.

Оба набора данных имеют средний балл на экзамене 81. Средние значения различаются незначительно: у первого класса средний балл на экзамене составляет 80,65, у второго класса средний балл на экзамене 80,65, а у второго класса средний балл на экзамене составляет 80,65. 80.65′ обзор 80.25.

Это говорит нам о том, что «базовый» или «типичный» балл на экзамене между двумя классами аналогичен.

Вывод 2: Первый набор данных имеет гораздо больший «разброс» значений.

Ряд показателей говорят нам о том, что результаты экзаменов первого класса разбросаны гораздо сильнее, чем результаты экзаменов второго класса.

Например, область применения класса 1 гораздо выше:

• Диапазон класса 1: 96 – 65 = 31
• Диапазон класса 2: 91 – 71 = 20

Межквартильный размах 1 класса также значительно выше:

• Интерквартильный размах 1 класса: 90,25 – 71 = 19,25.
• Интерквартильный размах 2 класса: 84,25 – 74,75 = 9,5.

Стандартное отклонение класса 1 также намного выше:

• Стандартное отклонение класса 1: 10,21.
• Стандартное отклонение класса 2: 6,43.

Каждый из этих показателей говорит нам о том, что разрыв в экзаменационных баллах у учащихся 1 класса намного выше, чем у учащихся 2 класса.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные операции в Excel:

Как создать сводную таблицу в Excel
Как рассчитать медиану по группе в Excel
Как рассчитать стандартное отклонение и игнорировать ноль в Excel