Т-критерий стьюдента

К бенджамин андерсон 3 августа, 2023 Статистика 0 комментариев

В этой статье объясняется, что такое t-критерий Стьюдента и для чего он используется в статистике. Таким образом, вы узнаете, как проводится t-критерий Стьюдента, какие существуют типы t-тестов Стьюдента и формулу для каждого из них.

Что такое t-критерий Стьюдента?

T-критерий Стьюдента , также называемый T-тестом или просто t-критерием , представляет собой статистический тест, в котором статистика теста соответствует t-распределению Стьюдента . Поэтому в статистике t-критерий Стьюдента используется для отклонения или принятия нулевой гипотезы проверки гипотезы.

В частности, t-критерий Стьюдента используется при проверке гипотез , при которой изучаемая совокупность подчиняется нормальному распределению, но размер выборки слишком мал, чтобы узнать дисперсию совокупности.

Короче говоря, t-критерий Стьюдента используется для отклонения или принятия гипотезы исследования определенных тестов гипотез. Например, t-критерий Стьюдента используется для проверки гипотез для одной выборки, для независимых выборок или для связанных выборок. Затем мы увидим, как рассчитывается критерий Стьюдента в каждом случае.

Виды t-тестов Стьюдента

Существует три типа t-тестов Стьюдента :

Одновыборочный t-критерий Стьюдента — используется для проверки гипотезы о значении выборочного среднего.
Критерий Стьюдента для двух независимых выборок : позволяет проверить гипотезу о разнице между средними значениями двух независимых выборок.
Критерий Стьюдента для двух парных выборок (или связанных выборок) – используется для проверки гипотезы о среднем значении выборки, проверенной дважды.

Образец t-критерия Стьюдента

Проверка гипотезы выборочного среднего значения — это проверка гипотезы, в которой нулевая гипотеза и альтернативная гипотеза теста что-то говорят о значении генерального среднего значения.

Формула одновыборочного t-критерия Стьюдента выглядит следующим образом:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

Золото:

$t$

— это статистика проверки гипотезы для среднего значения, которое определяется t-распределением Стьюдента.
$\overline{x}$

это образец означает.
$\mu$

— значение среднего значения, предложенного при проверке гипотезы.
$s$

— выборочное стандартное отклонение.
$n$

это размер выборки.

После того, как значение t-критерия Стьюдента рассчитано, результат статистического теста с критическим значением должен быть интерпретирован для отклонения или отклонения нулевой гипотезы:

Если проверка гипотезы о среднем является двусторонней, нулевая гипотеза отклоняется, если абсолютное значение t-критерия Стьюдента превышает критическое значение t _α/2|n-1 .
Если проверка гипотезы для среднего значения соответствует правому хвосту, нулевая гипотеза отклоняется, если значение t-критерия Стьюдента больше критического значения t _α|n-1 .
Если проверка гипотезы для среднего значения соответствует левому хвосту, нулевая гипотеза отклоняется, если значение t-критерия Стьюдента меньше критического значения -t _α|n-1 .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Обратите внимание, что критические значения теста получены из таблицы распределения Стьюдента.

➤ См.: Конкретный пример проверки гипотезы для среднего значения.

Критерий Стьюдента для независимых выборок

Критерий Стьюдента для независимых выборок используется, чтобы отвергнуть или принять гипотезу о взаимосвязи между средними значениями двух популяций, например, что средние значения двух популяций различны или что среднее значение генеральной совокупности A больше, чем среднее значение . население Б.

Однако в этом случае формула t-критерия Стьюдента варьируется в зависимости от того, можно ли считать дисперсии совокупности равными или нет. Затем мы увидим два возможных случая.

Неизвестные и равные отклонения

Формула для расчета t-критерия Стьюдента для независимых выборок, когда генеральные дисперсии неизвестны, но считаются равными, выглядит следующим образом:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Золото:

$t$

— это статистика проверки гипотезы для разницы средних значений с неизвестными дисперсиями, которая соответствует t-распределению Стьюдента с n ₁ + n ₂ -2 степенями свободы.
$\mu_1$

является средним значением численности населения 1.
$\mu_2$

является средним значением численности населения 2.
$\overline{x_1}$

является средним значением образца 1.
$\overline{x_2}$

является средним значением образца 2.
$s_p$

— объединенное стандартное отклонение.
$n_1$

размер выборки 1.
$n_2$

размер выборки 2.

Объединенное стандартное отклонение двух выборок рассчитывается по следующей формуле:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Неизвестные и разные вариации

Когда популяционные дисперсии неизвестны и, тем более, предполагаются разными, формула расчета t-критерия Стьюдента для независимых выборок выглядит следующим образом:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

Золото:

$t$

— это статистика проверки гипотезы для разницы средних значений с неизвестными дисперсиями, которая соответствует t-распределению Стьюдента.
$\mu_1$

является средним значением численности населения 1.
$\mu_2$

является средним значением численности населения 2.
$\overline{x_1}$

является средним значением образца 1.
$\overline{x_2}$

является средним значением образца 2.
$\sigma_1$

— стандартное отклонение генеральной совокупности 1.
$\sigma_2$

— стандартное отклонение генеральной совокупности 2.
$n_1$

размер выборки 1.
$n_2$

размер выборки 2.

Однако в этом случае степени свободы t-распределения Стьюдента рассчитываются по следующей формуле:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ См.: Конкретный пример проверки гипотезы о разнице средних значений.

Критерий Стьюдента для парных или связанных выборок

Этот тест используется, когда две изучаемые выборки связаны друг с другом, так что фактически это одна выборка особей, которая анализировалась дважды (каждый раз в разных условиях).

Например, вы можете проанализировать оценки учащихся по курсу математики и статистики, чтобы увидеть, существует ли значительная разница между средними показателями по двум предметам. В этом случае оценка каждого учащегося по математике связана с оценкой того же учащегося по статистике.

Формула t-критерия Стьюдента для парных или связанных выборок :

$\displaystyle t=\frac{\overline{x_D}-\mu_D}{\displaystyle \frac{s_D}{\sqrt{n}}}$

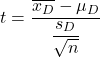
Золото:

$t$

— это статистика проверки гипотез для парных средних, которая определяется t-распределением Стьюдента.
$\overline{x_D}$

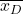
— среднее значение выборки, образованной разницей данных.
$\mu_D$

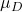
— значение среднего значения, предложенного при проверке гипотезы.
$s_D$

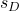
— стандартное отклонение выборки, образованное разницей данных.
$n$

это размер выборки.

Предположения t-теста Стьюдента

Для проведения t-критерия Стьюдента должны быть выполнены следующие условия:

Непрерывность – данные выборки непрерывны.
Случайность : выборки данных были выбраны случайным образом.
Однородность : дисперсия выборки данных однородна.
Нормальность – распределение, определяющее выборку данных, примерно нормальное.

Как пройти t-тест Стьюдента

Наконец, вкратце, подробно описаны шаги, которые необходимо выполнить для проведения t-критерия Стьюдента.

Определите нулевую и альтернативную гипотезы проверки гипотез.
Установите уровень значимости (α) проверки гипотезы.
Убедитесь, что предположения t-критерия Стьюдента выполняются.
Примените соответствующую формулу t-критерия Стьюдента и рассчитайте статистику теста.
Интерпретируйте результат t-критерия Стьюдента, сравнив его с критическим значением теста.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Что такое t-критерий Стьюдента?

Виды t-тестов Стьюдента

Образец t-критерия Стьюдента

Критерий Стьюдента для независимых выборок

Неизвестные и равные отклонения

Неизвестные и разные вариации

Критерий Стьюдента для парных или связанных выборок

Предположения t-теста Стьюдента

Как пройти t-тест Стьюдента

Об авторе

бенджамин андерсон

Добавить комментарий