Как рассчитать стьюдентизированные остатки в python
Остаток студента — это просто остаток, разделенный на его расчетное стандартное отклонение.
На практике мы обычно говорим, что любое наблюдение в наборе данных, у которого остаток студента превышает абсолютное значение 3, является выбросом.
Мы можем быстро получить стьюдентизированные остатки модели регрессии в Python, используя функцию OLSResults.outlier_test() statsmodels, которая использует следующий синтаксис:
OLSResults.outlier_test()
где OLSResults — имя линейной модели, подобранной с помощью функции statsmodels ols() .
Пример: расчет стьюдентизированных остатков в Python
Предположим, мы создаем следующую простую модель линейной регрессии на Python:
#import necessary packages and functions import numpy as np import pandas as pd import statsmodels. api as sm from statsmodels. formula . api import ols #create dataset df = pd. DataFrame ({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86], 'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19]}) #fit simple linear regression model model = ols('rating ~ points', data=df). fit ()
Мы можем использовать функцию outlier_test() для создания DataFrame, содержащего стьюдентизированные остатки для каждого наблюдения в наборе данных:
#calculate studentized residuals stud_res = model. outlier_test () #display studentized residuals print(stud_res) student_resid unadj_p bonf(p) 0 -0.486471 0.641494 1.000000 1 -0.491937 0.637814 1.000000 2 0.172006 0.868300 1.000000 3 1.287711 0.238781 1.000000 4 0.106923 0.917850 1.000000 5 0.748842 0.478355 1.000000 6 -0.968124 0.365234 1.000000 7 -2.409911 0.046780 0.467801 8 1.688046 0.135258 1.000000 9 -0.014163 0.989095 1.000000
Этот DataFrame отображает следующие значения для каждого наблюдения в наборе данных:
- Стьюдентизированный остаток
- Нескорректированное значение p стьюдентизированного остатка
- Скорректированное Бонферрони p-значение остатка студента
Мы видим, что стьюдентизированный остаток для первого наблюдения в наборе данных равен -0,486471 , стьюдентизированный остаток для второго наблюдения равен -0,491937 и так далее.
Мы также можем создать быстрый график значений переменных-предикторов в сравнении с соответствующими стьюдентизированными остатками:
import matplotlib. pyplot as plt #define predictor variable values and studentized residuals x = df[' points '] y = stud_res[' student_resid '] #create scatterplot of predictor variable vs. studentized residuals plt. scatter (x,y) plt. axhline (y=0, color=' black ', linestyle=' -- ') plt. xlabel (' Points ') plt. ylabel (' Studentized Residuals ')
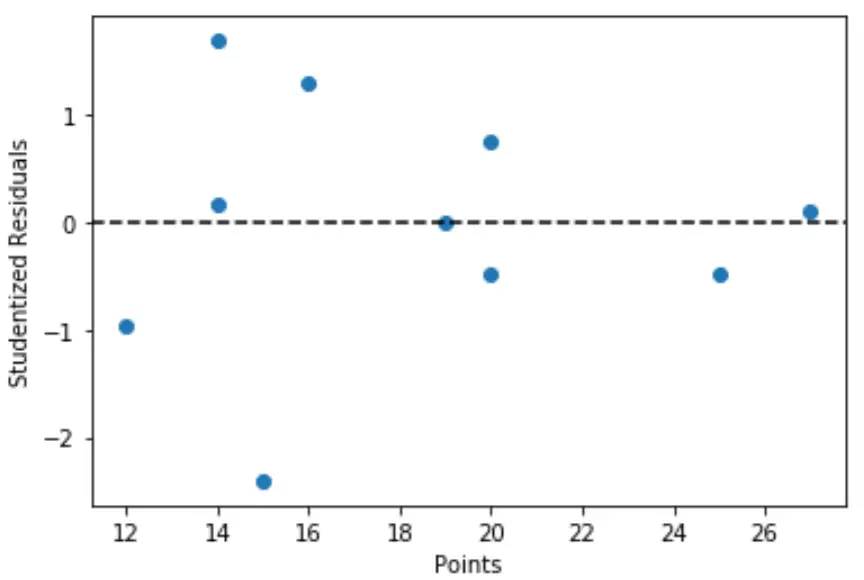
На графике мы видим, что ни одно из наблюдений не имеет остатка Стьюдента с абсолютным значением больше 3, поэтому в наборе данных нет явных выбросов.
Дополнительные ресурсы
Как выполнить простую линейную регрессию в Python
Как выполнить множественную линейную регрессию в Python
Как создать остаточный график в Python