Теорема байеса

К бенджамин андерсон 1 августа, 2023 Вероятность 0 комментариев

В этой статье объясняется, что такое теорема Байеса и для чего она используется в теории вероятности и статистике. Таким образом, вы узнаете, какова формула теоремы Байеса, решены примеры теоремы Байеса и каковы применения этой теоремы.

Что такое теорема Байеса?

В теории вероятностей теорема Байеса — это закон, используемый для расчета вероятности события, когда априорная информация об этом событии известна.

Более конкретно, теорема Байеса математически связывает вероятность события A при условии события B с вероятностью события B при условии A.

Например, если вы заранее знаете вероятность того, что у человека будет головная боль во время гриппа, вы можете использовать теорему Байеса, чтобы определить вероятность того, что человек заболеет гриппом, когда у него болит голова.

Теорема Байеса имеет множество применений, например, она используется в медицине, экономике или технике для расчета вероятностей определенных событий, обусловленных другими событиями. Ниже мы подробно остановимся на различных применениях теоремы Байеса.

Теорема Байеса была изобретена английским математиком Томасом Байесом (1702–1761), хотя опубликована она была посмертно в 1763 году.

➤ См.: Условная вероятность.

Формула теоремы Байеса

Теорема Байеса гласит, что, учитывая выборочное пространство, состоящее из набора взаимоисключающих событий {A ₁ , A ₂ ,…, A _i ,…, _An }, вероятности которых не равны нулю, и другого события B , мы можем математически связать условное вероятность A _i с учетом события B с условной вероятностью B с учетом A _i .

Итак, формула теоремы Байеса , также известная как правило Байеса , выглядит так:

Золото:

$P(A_i|B)$

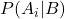
— это условная вероятность события A _при данном событии B, называемая апостериорной вероятностью.
$P(B|A_i)$

— условная вероятность события B при данном событии A _i .
$P(A_i)$

— это вероятность того, что событие A _i произойдет, называемая априорной вероятностью.

Обратите внимание, что знаменателем формулы теоремы Байеса является полная вероятность события B.

Пример теоремы Байеса

Как только мы увидим определение теоремы Байеса и ее формулу, мы увидим решенный пример того, как вероятность рассчитывается с помощью теоремы Байеса, чтобы лучше понять эту концепцию.

В магазине электроники продаются телевизоры трех марок: X, Y, Z. Подсчитано, что 20% продаж составляют телевизоры марки Y с дефектами, 3% телевизоров марки Y с дефектами и 4% телевизоров марки Z с дефектами. Учитывая неисправный телевизор, какова вероятность того, что это телевизор марки Z?

Это упражнение дает нам вероятность того, что покупатель купит телевизор каждой марки:

Событие _A1 : Покупатель покупает телевизор марки X → P( _A1 )=0,20.
Событие _A2 : Покупатель покупает телевизор марки Y → P( _A2 )=0,50.
Событие _A3 : Покупатель покупает телевизор марки Z → P( _A3 )=0,30.

Кроме того, показания также дают нам вероятность того, что телевизор каждой марки неисправен:

Событие Б: Телевизор неисправен.

B|A ₁ : Учитывая телевизор марки X, телевизор неисправен → P(B|A ₁ ) = 0,05.
B|A ₂ : Учитывая телевизор марки Y, телевизор неисправен → P(B|A ₂ )=0,03.
B|A ₃ : Учитывая телевизор марки Z, телевизор неисправен → P(B|A ₃ )=0,04.

Итак, дерево вероятностей всех интересующих нас событий выглядит следующим образом:

Итак, чтобы вычислить вероятность того, что, учитывая дефектный телевизор, это марка Z, мы должны использовать формулу из теоремы Байеса:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

Используя терминологию, используемую в этом примере, формула Байеса выглядит следующим образом:

$P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}$

Таким образом, расчет вероятности того, что данный неисправный телевизор будет марки Z, выглядит следующим образом:

$\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}$

В заключение вероятность того, что если телевизор неисправен, то это марка Z, составляет 32%.

Приложения теоремы Байеса

Существует множество применений теоремы Байеса, в том числе:

Медицинские тесты . Теорема Байеса часто используется в медицине для определения вероятности прохождения диагностических тестов. Например, в случае теста на ВИЧ теорему можно использовать для расчета вероятности того, что у человека действительно есть вирус, если результат теста положительный.
Финансовый анализ . В финансах теорема Байеса используется для расчета вероятности того, что определенные экономические события, такие как увеличение или уменьшение стоимости акций, произойдут с учетом набора экономических переменных.
Исследование рынка : Теорема Байеса позволяет определить, например, вероятность того, что человек купит товар, увидев рекламу этого товара.
Прогноз погоды . Модели погоды также используют теорему Байеса для определения вероятности того, что данный прогноз погоды, основанный на данных наблюдений, сбудется. Это повышает точность климатических прогнозов.
Компьютерная безопасность . В сфере кибербезопасности теорема Байеса может применяться для определения вероятности того, что подозрительная деятельность действительно является атакой на компьютерную систему.

Решенные задачи по теореме Байеса

Упражнение 1

По оценкам, 1% населения страдает каким-либо заболеванием. Тест на выявление этого заболевания имеет точность 95% для положительных случаев и 90% для отрицательных случаев. Если у случайно выбранного человека результат теста окажется положительным, какова вероятность того, что он действительно болен?

Посмотреть решение

Оператор упражнения дает нам следующие вероятности:

A ₁ : У человека имеется заболевание → P(A ₁ )=0,01.
_A2 : У человека нет заболевания → P( _A2 )=0,99.

Б: Тест положительный
B|A ₁ : Тест положительный, если у человека имеется заболевание → P(B|A ₁ ) = 0,95.
B|A ₂ : Тест положительный, если у человека нет заболевания → P(B|A ₂ )=1-0,90=0,10.

Затем, чтобы вычислить вероятность того, что случайно выбранный человек действительно болен заболеванием при положительном результате теста, необходимо применить правило Байеса:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

$P(A_1|B)=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}$

Итак, подставляем значения в формулу и выполняем расчет вероятности:

$\begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}$

Короче говоря, вероятность того, что случайно выбранный человек получит положительный результат теста и действительно заболеет, составляет 8,76%.

Упражнение 2

Подсчитано, что вероятность того, что акция вырастет за один день, составляет 40 %, что она останется стабильной — 10 %, а что она упадёт — 50 %. Более того, мы знаем, что когда рынок растет, вероятность того, что финансовый аналитик правильно предскажет его, составляет 90%, что, когда рынок остается стабильным, вероятность того, что прогноз окажется правильным, составляет 75%, а в случае спада вероятность правильного прогноза составляет 75%. 85%.%. Если аналитик предсказывает, что рынок упадет, насколько вероятно, что он действительно упадет?

Посмотреть решение

В этом случае оператор выполнения предоставляет нам следующие вероятности:

A ₁ : Рынок растет за один день → P(A ₁ ) = 0,40.
_A2 : Рынок остается стабильным в течение одного дня → P( _A2 )=0,10.
_A3 : Рынок растет за один день → P( _A3 )=0,50.

Б: Аналитик предсказывает, что рынок упадет.
B|A ₁ : Аналитик правильно предсказывает, что рынок вырастет → P(B|A ₁ )=0,90.
B|A ₂ : Аналитик правильно прогнозирует, что рынок останется стабильным → P(B|A ₂ )=0,75.
B|A ₃ : Аналитик правильно предсказывает, что рынок упадет → P(B|A ₃ )=0,85.

Чтобы определить вероятность того, что аналитик сделает прогноз падения рынка и что он окажется верным, нам нужно использовать формулу теоремы Байеса:

$P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}$

$P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}$

Подставляем значения вероятности в формулу Байеса и вычисляем вероятность:

$\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}$

Следовательно, вероятность того, что аналитик прав, когда говорит, что фондовый рынок упадет, составляет 49,42%.

Об авторе

бенджамин андерсон

Здравствуйте, я Бенджамин, профессор статистики на пенсии, ставший преданным преподавателем Statorials. Имея обширный опыт и знания в области статистики, я хочу поделиться своими знаниями, чтобы расширить возможности студентов с помощью Statorials. Узнать больше

Что такое теорема Байеса?

Формула теоремы Байеса

Пример теоремы Байеса

Приложения теоремы Байеса

Решенные задачи по теореме Байеса

Упражнение 1

Упражнение 2

Об авторе

бенджамин андерсон

Добавить комментарий