Как применить теорему чебышева в excel
Теорема Чебышева утверждает, что для любого числа k больше 1 по крайней мере 1 – 1/k 2 значений данных в любом обученном распределении лежит в пределах k стандартных отклонений от среднего значения.
Например, для любого фигурного распределения как минимум 1 – 1/3 2 = 88,89% значений в распределении попадут в пределы 3 стандартных отклонений от среднего значения.
В этом уроке показано несколько примеров применения теоремы Чебышева в Excel.
Пример 1. Используйте теорему Чебышева, чтобы определить, какой процент значений попадет в диапазон от 30 до 70 для набора данных со средним значением 50 и стандартным отклонением 10.
Сначала определите значение k. Мы можем сделать это, определив, сколько стандартных отклонений находится между 30 и 70 от среднего значения:
(30 – среднее) / стандартное отклонение = (30 – 50) / 10 = -20 / 10 = -2
(70 – среднее) / стандартное отклонение = (70 – 50) / 10 = 20 / 10 = 2
Значения 30 и 70 — это на 2 стандартных отклонения ниже и выше среднего соответственно. Итак, к = 2 .
Затем мы можем использовать следующую формулу в Excel, чтобы найти минимальный процент значений, попадающих в пределах двух стандартных отклонений от среднего значения для этого набора данных:
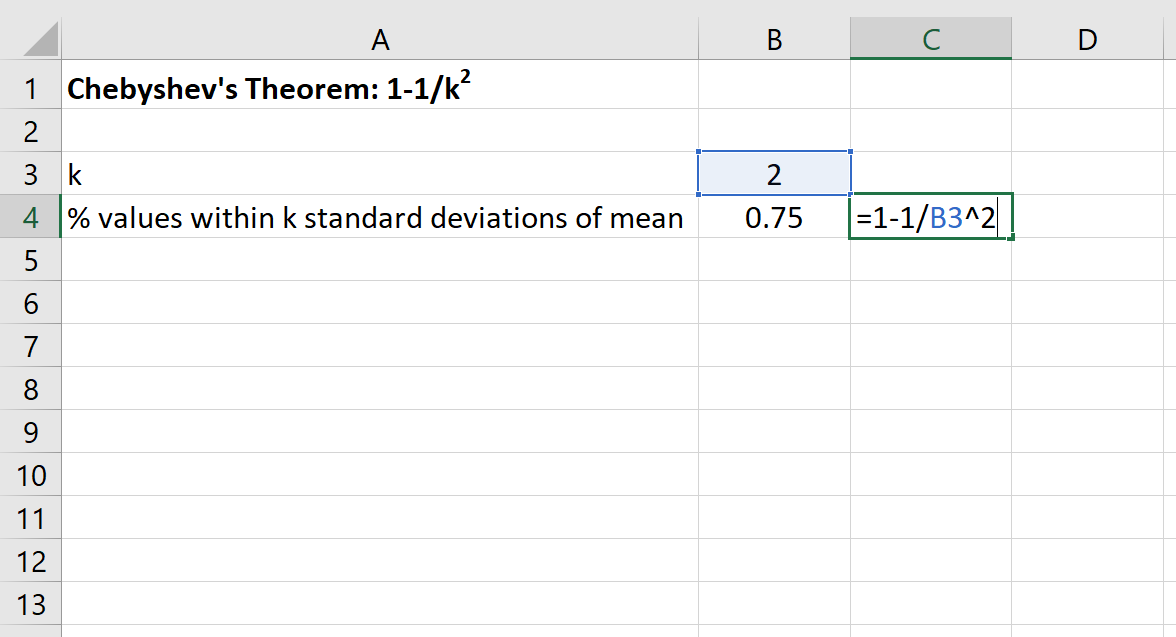
Процент значений между 30 и 70 для этого набора данных составит не менее 75% .
Пример 2. Используйте теорему Чебышева, чтобы определить, какой процент значений попадет в диапазон от 20 до 50 для набора данных со средним значением 35 и стандартным отклонением 5.
Сначала определите значение k. Мы можем сделать это, определив, сколько стандартных отклонений находится между 20 и 50 от среднего значения:
(20 – среднее) / стандартное отклонение = (20 – 35) / 5 = -15 / 5 = -3
(50 – среднее) / стандартное отклонение = (50 – 35) / 5 = 15 / 5 = 3
Значения 20 и 50 — это на 3 стандартных отклонения ниже и выше среднего соответственно. Итак, к = 3 .
Затем мы можем использовать следующую формулу в Excel, чтобы найти минимальный процент значений, попадающих в пределах 3 стандартных отклонений от среднего значения для этого набора данных:
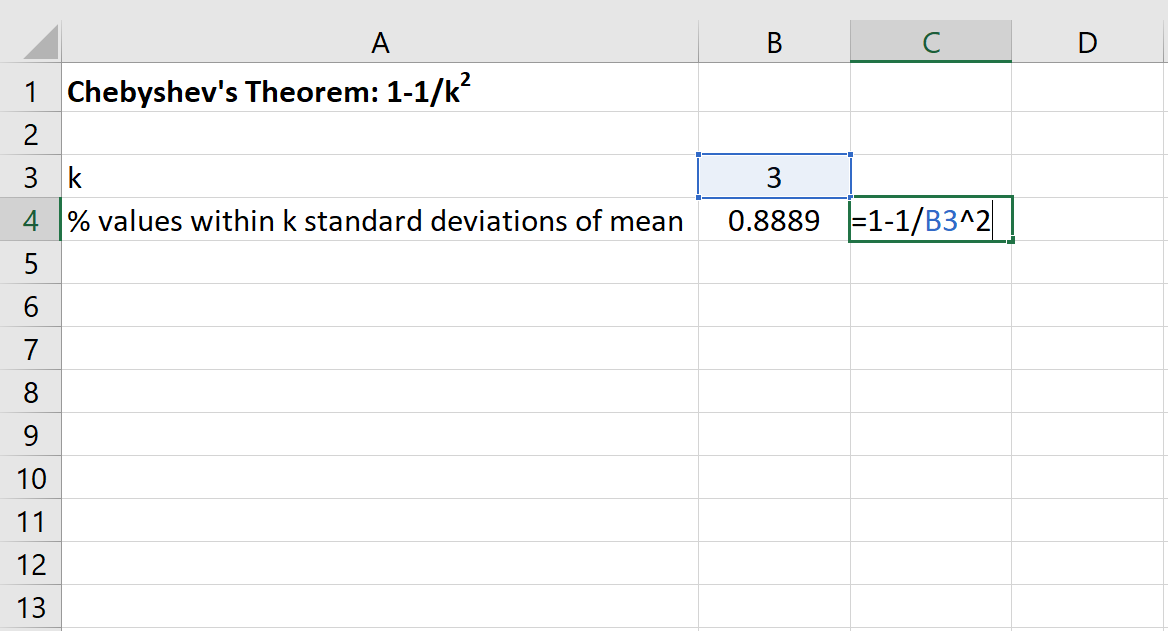
Процент значений между 20 и 50 для этого набора данных составит не менее 88,89% .
Пример 3. Используйте теорему Чебышева, чтобы определить, какой процент значений попадет в диапазон от 80 до 120 для набора данных со средним значением 100 и стандартным отклонением 5.
Сначала определите значение k. Мы можем сделать это, определив, сколько стандартных отклонений находится между 80 и 120 от среднего значения:
(80 – среднее) / стандартное отклонение = (80 – 100) / 5 = -20 / 5 = -4
(120 – среднее) / стандартное отклонение = (120 – 100) / 5 = 20 / 5 = 4
Значения 80 и 120 — это на 4 стандартных отклонения ниже и выше среднего соответственно. Итак, к = 4 .
Затем мы можем использовать следующую формулу в Excel, чтобы найти минимальный процент значений, попадающих в пределах 4 стандартных отклонений от среднего значения для этого набора данных:
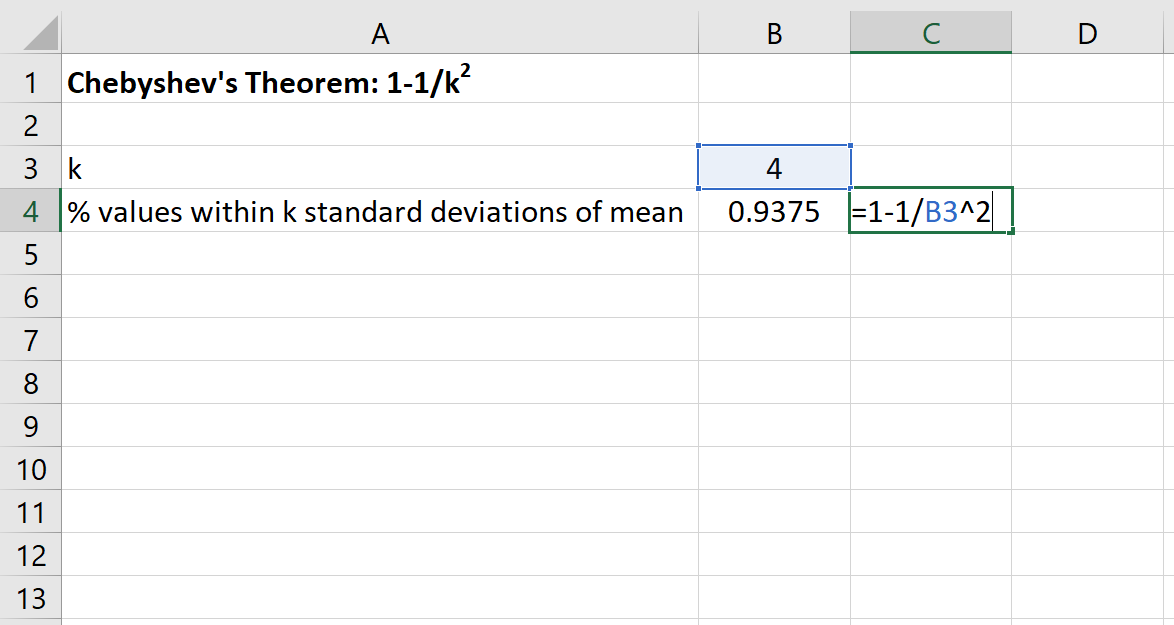
Процент значений между 80 и 120 для этого набора данных составит не менее 93,75% .