Критерий бартлетта на однородность дисперсий (определение и пример)
Тест Бартлетта — это статистический тест, используемый для определения того, равны ли дисперсии между несколькими группами.
Многие статистические тесты (например , однофакторный дисперсионный анализ ) предполагают, что дисперсии между выборками равны. Для проверки этой гипотезы можно использовать тест Бартлетта.
Следующие шаги объясняют, как выполнить тест Бартлетта.
Примечание. Не путайте этот тест с тестом сферичности Бартлетта , который используется для сравнения наблюдаемой корреляционной матрицы с единичной матрицей.
Шаги по выполнению теста Бартлетта
Тест Бартлетта использует следующие нулевые и альтернативные гипотезы :
H 0 : Разница между каждой группой одинакова.
Х А : По крайней мере, в одной группе есть дисперсия, не равная остальным.
Статистику теста можно рассчитать следующим образом:
B = (nk)lns 2 – Σ(n j -1)lns j 2 / c
Золото:
- n: общее количество наблюдений во всех группах
- k: Общее количество групп
- ln: Это означает «натуральное бревно».
- s 2 : Объединенная дисперсия
- n j : Количество наблюдений в группе j.
- s j 2 : Дисперсия группы j
И где он рассчитывается следующим образом:
- c = 1 + (1/3(k-1))*(Σ(1/(n j -1)) – (1/(nk))
Эта тестовая статистика соответствует распределению Хи-квадрат с k-1 степенями свободы. Другими словами, B ~ X 2 (k-1).
Если значение p , соответствующее тестовой статистике, ниже определенного уровня значимости (например, α = 0,05), то мы можем отвергнуть нулевую гипотезу и сделать вывод, что не все группы имеют одинаковую дисперсию.
Пример: тест Бартлетта
Предположим, профессор хочет знать, приводят ли три разных метода обучения к разным средним оценкам на экзаменах.
Она случайным образом поручает 10 ученикам использовать каждую технику в течение недели, а затем дает каждому ученику экзамен равной сложности.
Результаты экзаменов 30 студентов представлены ниже:

Профессор хочет выполнить однофакторный дисперсионный анализ, чтобы увидеть, приводят ли три метода к разным средним баллам на экзамене, но сначала она должна выполнить тест Бартлетта, чтобы убедиться, что три группы имеют равные отклонения.
Выполнять тест Бартлетта вручную утомительно, поэтому введем в калькулятор теста Бартлетта следующие значения данных:
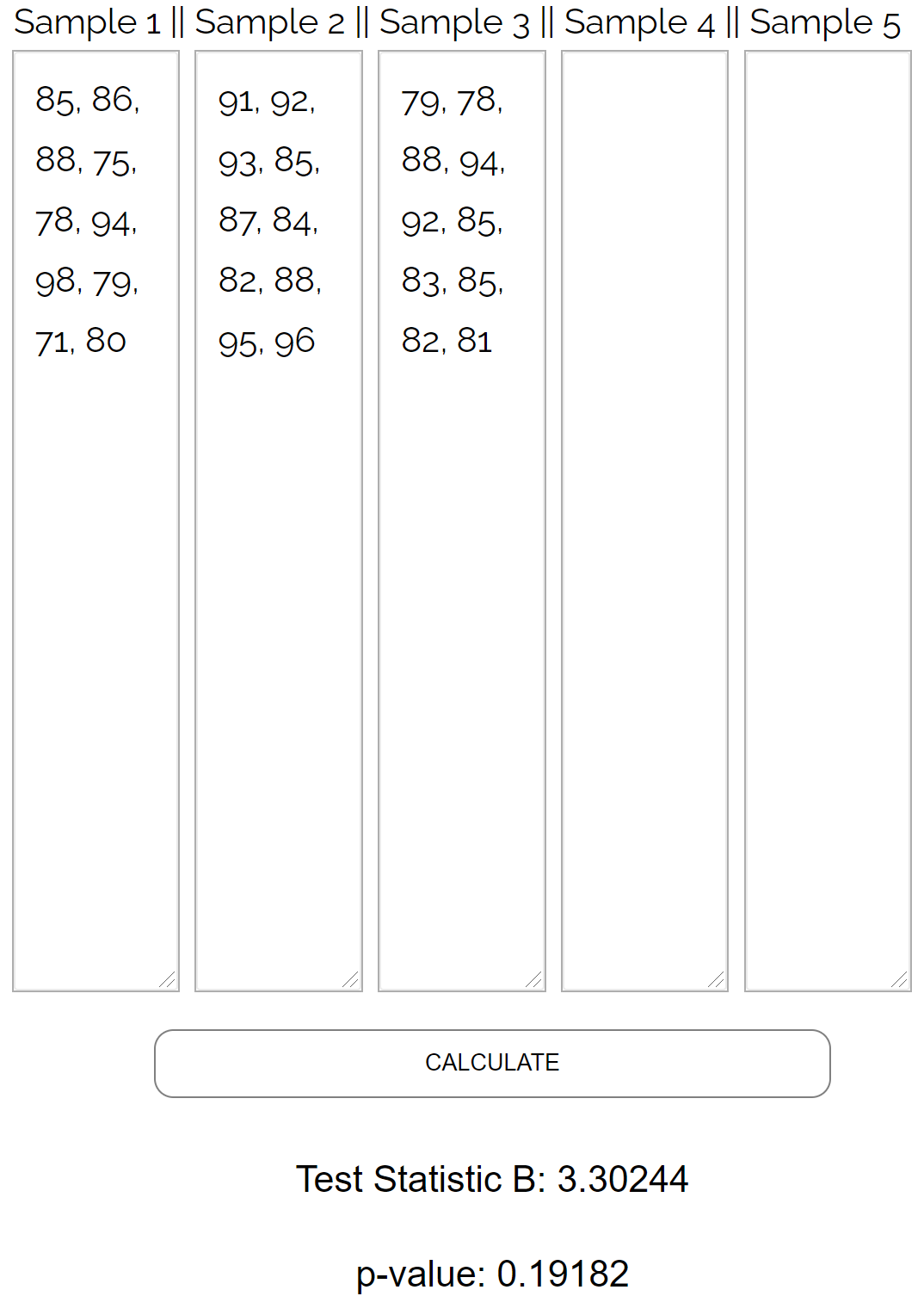
Тест возвращает следующие результаты:
- Статистика теста B : 3,30244
- P-значение: 0,19182
Поскольку значение p не меньше 0,05, профессор не сможет отвергнуть нулевую гипотезу. Другими словами, у нее нет достаточных доказательств, чтобы сказать, что в трех группах есть разные пробелы.
Таким образом, она может приступить к выполнению одностороннего дисперсионного анализа.
Дополнительные ресурсы
Как выполнить тест Бартлетта в R (шаг за шагом)
Как выполнить тест Бартлетта на Python (шаг за шагом)