Как использовать тест даннета для множественных сравнений

ANOVA (дисперсионный анализ) используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более независимых групп.

Если p-значение ANOVA ниже определенного выбранного уровня значимости, мы можем отвергнуть нулевую гипотезу и заключить, что у нас есть достаточные доказательства, чтобы сказать, что по крайней мере одно из групповых средних значений отличается от других.

Однако это не говорит нам о том, какие группы отличаются друг от друга. Это просто говорит нам о том, что не все средние значения по группам одинаковы. Чтобы точно знать, какие группы отличаются друг от друга, нам нужно провести апостериорный тест .

Если одна из групп в исследовании считается контрольной , то нам следует использовать критерий Даннетта в качестве апостериорного теста после ANOVA.

Тест Даннетта: определение

Для выполнения теста Даннетта мы можем использовать следующие два шага:

Шаг 1: Найдите критическое значение Даннета.

Во-первых, нам нужно найти критическое значение Даннетта. Это рассчитывается следующим образом:

Критическое значение Даннетта: t _d √ 2MS _w /n

Золото:

• t _d : значение, найденное в таблице Даннетта для данного альфа-уровня, количества групп и размеров групповой выборки.
• MS _w : средние квадраты «внутри группы» в выходной таблице ANOVA.
• n: Размер групповой выборки

Шаг 2: Сравните различия между групповыми средними значениями с критическим значением Даннета.

Затем мы вычисляем абсолютную разницу между средним значением каждой группы и средним значением контрольной группы. Если разница превышает критическое значение Даннета, то эту разницу называют статистически значимой.

В следующем примере показано, как выполнить тест Даннетта на практике.

Тест Даннетта: пример

Предположим, учитель хочет знать, могут ли два новых метода обучения улучшить результаты тестов ее учеников. Чтобы проверить это, она случайным образом делит свой класс из 30 учеников на следующие три группы:

• Контрольная группа: 10 студентов.
• Новое техническое исследование 1: 10 студентов
• Новое техническое исследование 2: 10 студентов

После недели использования назначенной им методики обучения каждый студент сдает один и тот же экзамен. Результаты приведены ниже:

• Средний балл на экзамене контрольной группы: 81,6.
• Средний балл на экзамене для группы 1 по новой методике обучения: 85,8.
• Средний балл на групповом экзамене New Study Technique 2: 87,7.
• Средние квадраты «Внутри группы» в выходной таблице ANOVA: 23,3.

Обладая этой информацией, мы можем выполнить тест Даннетта, чтобы определить, дает ли один из двух новых методов обучения существенно отличающиеся средние баллы на экзамене от контрольной группы.

Шаг 1: Найдите критическое значение Даннета.

Используя α = 0,05, размер групповой выборки n = 10 и общее количество групп = 3, таблица Даннета рекомендует нам использовать значение 2,57 при расчете критического значения.

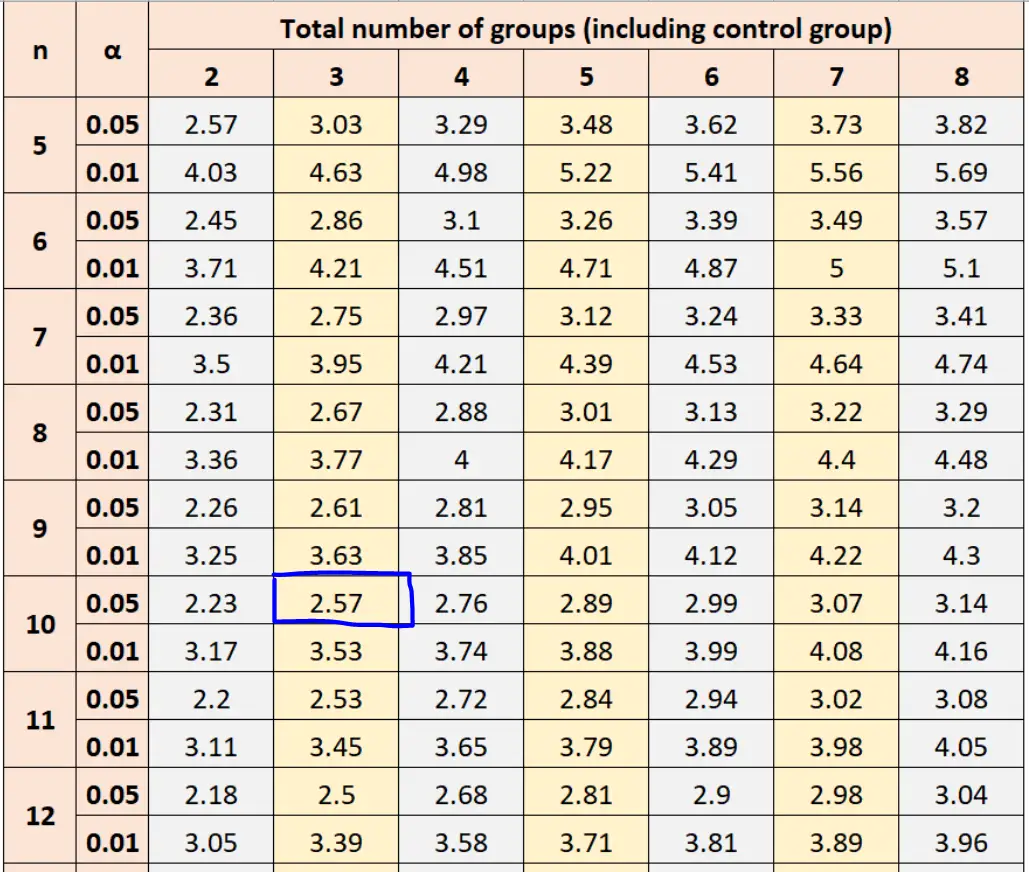
Затем мы можем подставить это число в формулу, чтобы найти критическое значение Даннетта:

Критическое значение Даннетта: t _d √ 2MS _w /n = 2,57√ 2(23,3)/10 = 5,548.

Шаг 2: Сравните различия между групповыми средними значениями с критическим значением Даннета.

Абсолютные различия между средствами каждого метода исследования и средствами контрольной группы следующие:

• Абс. разница между новым приемом 1 и контролем: |85,8 – 81,6| = 4,2
• Абс. разница между новым приемом 2 и контролем: |87,7 – 81,6| = 6,1

Только абсолютная разница между методом 2 и контрольной группой превышает критическое значение Даннетта, равное 5548 .

Таким образом, мы можем сказать, что новая методика обучения № 2 дает существенно отличающиеся результаты экзамена по сравнению с контрольной группой, но это не относится к новой методике обучения № 1.

Дополнительные ресурсы

Введение в однофакторный дисперсионный анализ
Руководство по использованию апостериорного тестирования с помощью ANOVA
Как выполнить тест Даннетта в R