Расширенный тест дики-фуллера в r (с примером)
Временной ряд называется «стационарным», если он не имеет тенденции, представляет постоянную дисперсию во времени и имеет постоянную автокорреляционную структуру во времени.
Один из способов проверить, является ли временной ряд стационарным, — это выполнить расширенный тест Дики-Фуллера , который использует следующие нулевые и альтернативные гипотезы:
H 0 : Временной ряд нестационарен. Другими словами, его структура зависит от времени, и ее изменение не является постоянным во времени.
Х А : Временной ряд стационарен.
Если значение p теста ниже определенного уровня значимости (например, α = 0,05), то мы можем отвергнуть нулевую гипотезу и сделать вывод, что временной ряд стационарен.
В следующем пошаговом примере показано, как выполнить расширенный тест Дики-Фуллера в R для заданного временного ряда.
Пример: расширенный тест Дики-Фуллера в R.
Предположим, у нас есть следующие данные временного ряда в R:
data <- c(3, 4, 4, 5, 6, 7, 6, 6, 7, 8, 9, 12, 10)
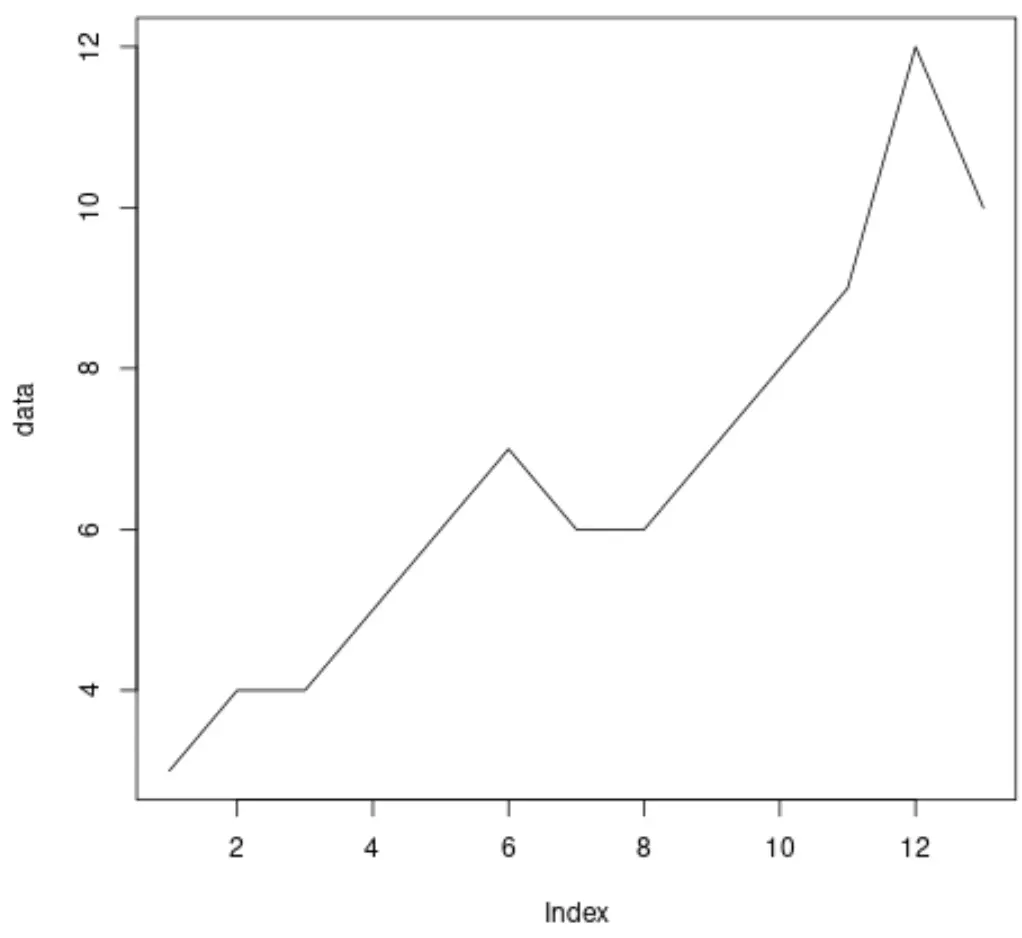
Прежде чем выполнять расширенный тест Дики-Фуллера для данных, мы можем создать быстрый график для визуализации данных:
plot(data, type=' l ')
Чтобы выполнить расширенный тест Дикки-Фуллера, мы можем использовать функцию adf.test() из библиотеки tseries .
Следующий код показывает, как использовать эту функцию:
library (tseries) #perform augmented Dickey-Fuller test adf.test(data) Augmented Dickey-Fuller Test data:data Dickey-Fuller = -2.2048, Lag order = 2, p-value = 0.4943 alternative hypothesis: stationary
Вот как интерпретировать наиболее важные значения результата:
- Статистика теста: -2,2048
- P-значение: 0,4943
Поскольку значение p не меньше 0,05, мы не можем отвергнуть нулевую гипотезу.
Это означает, что временной ряд не является стационарным. Другими словами, его структура зависит от времени, и ее изменение не является постоянным во времени.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в R:
Как выполнить тест тренда Манна-Кендалла в R
Как построить временной ряд в R
Как уменьшить тенденции данных