Как выполнить тест крускала-уоллиса в excel
Тест Крускала-Уоллиса используется для определения наличия или отсутствия статистически значимой разницы между медианами трех или более независимых групп. Он считается непараметрическим эквивалентом одностороннего дисперсионного анализа.
В этом руководстве объясняется, как выполнить тест Крускала-Уоллиса в Excel.
Пример: тест Крускала-Уоллиса в Excel
Исследователи хотят знать, приводят ли три разных удобрения к разным уровням роста растений. Они случайным образом выбирают 30 разных растений и делят их на три группы по 10, применяя к каждой группе разные удобрения. Через месяц измеряют высоту каждого растения.
Выполните следующие шаги, чтобы выполнить тест Крускала-Уоллиса и определить, одинаков ли медианный рост во всех трех группах.
Шаг 1: Введите данные.
Введите следующие данные, которые показывают общий рост (в дюймах) каждого из 10 растений в каждой группе:
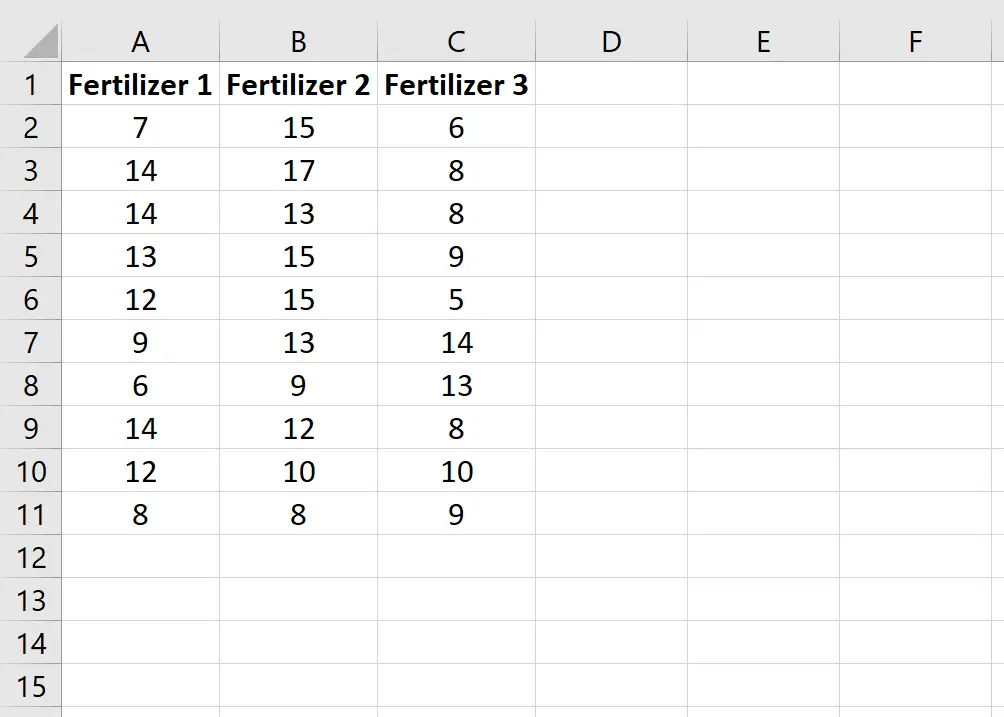
Шаг 2: Классифицируйте данные.
Далее мы воспользуемся функцией RANK.AVG() , чтобы присвоить ранг росту каждого растения среди 30 растений. Следующая формула показывает, как рассчитать ранг первого растения в первой группе:
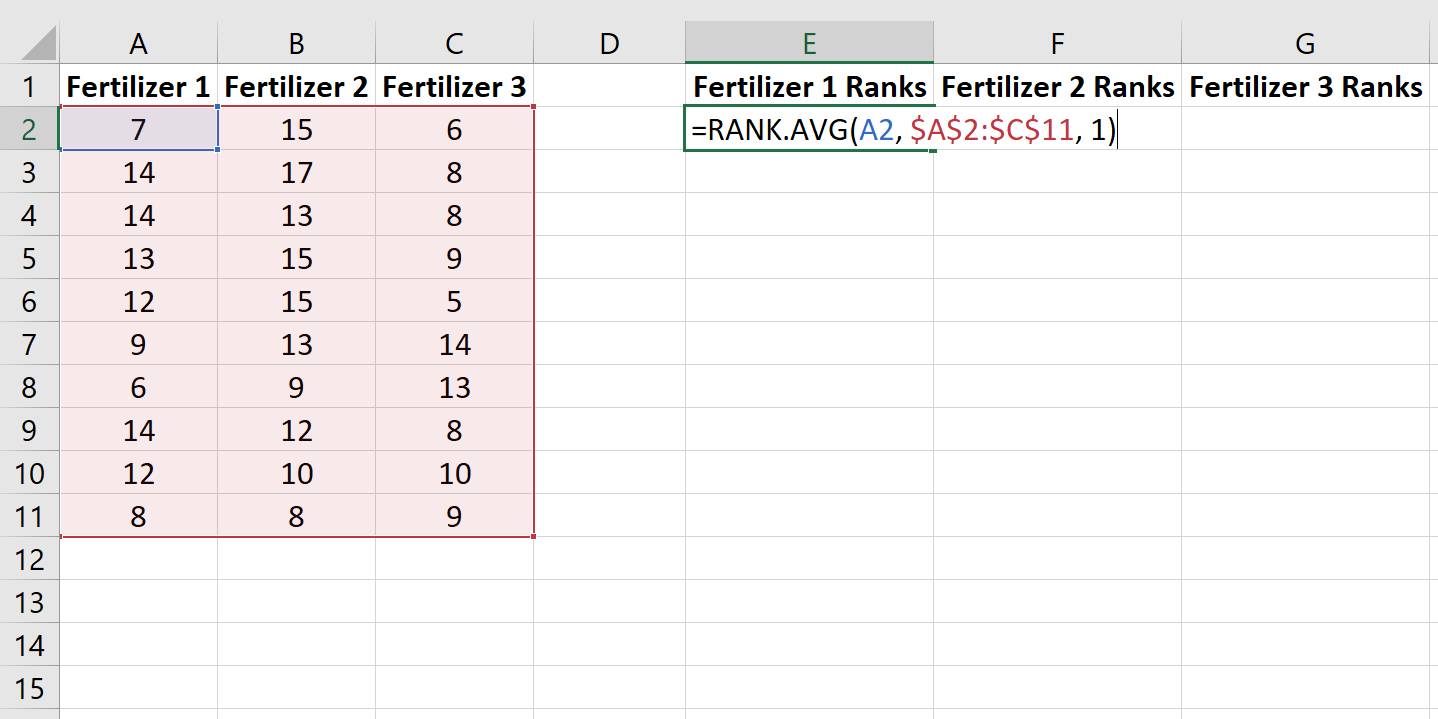
Скопируйте эту формулу в остальные ячейки:
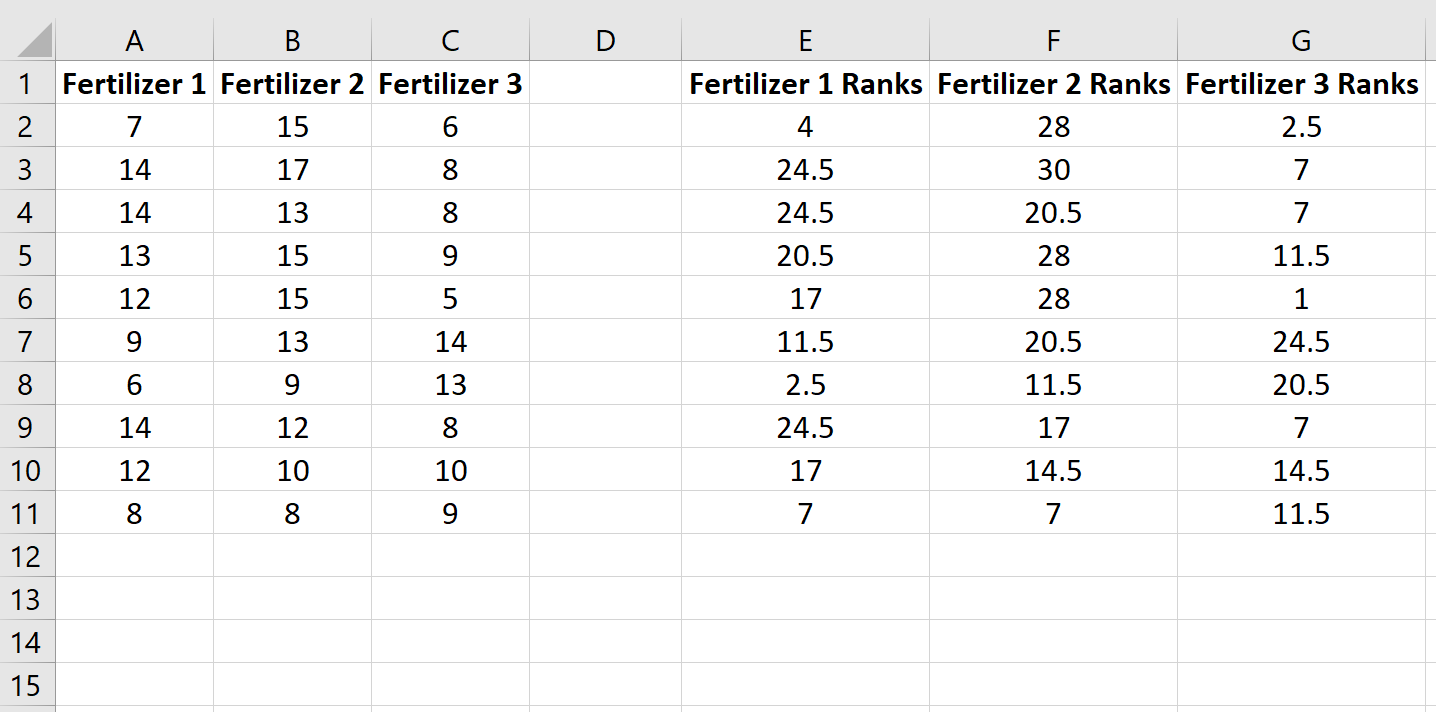
Затем вычислите сумму рангов для каждого столбца вместе с размером выборки и квадратом суммы рангов, разделенной на размер выборки:
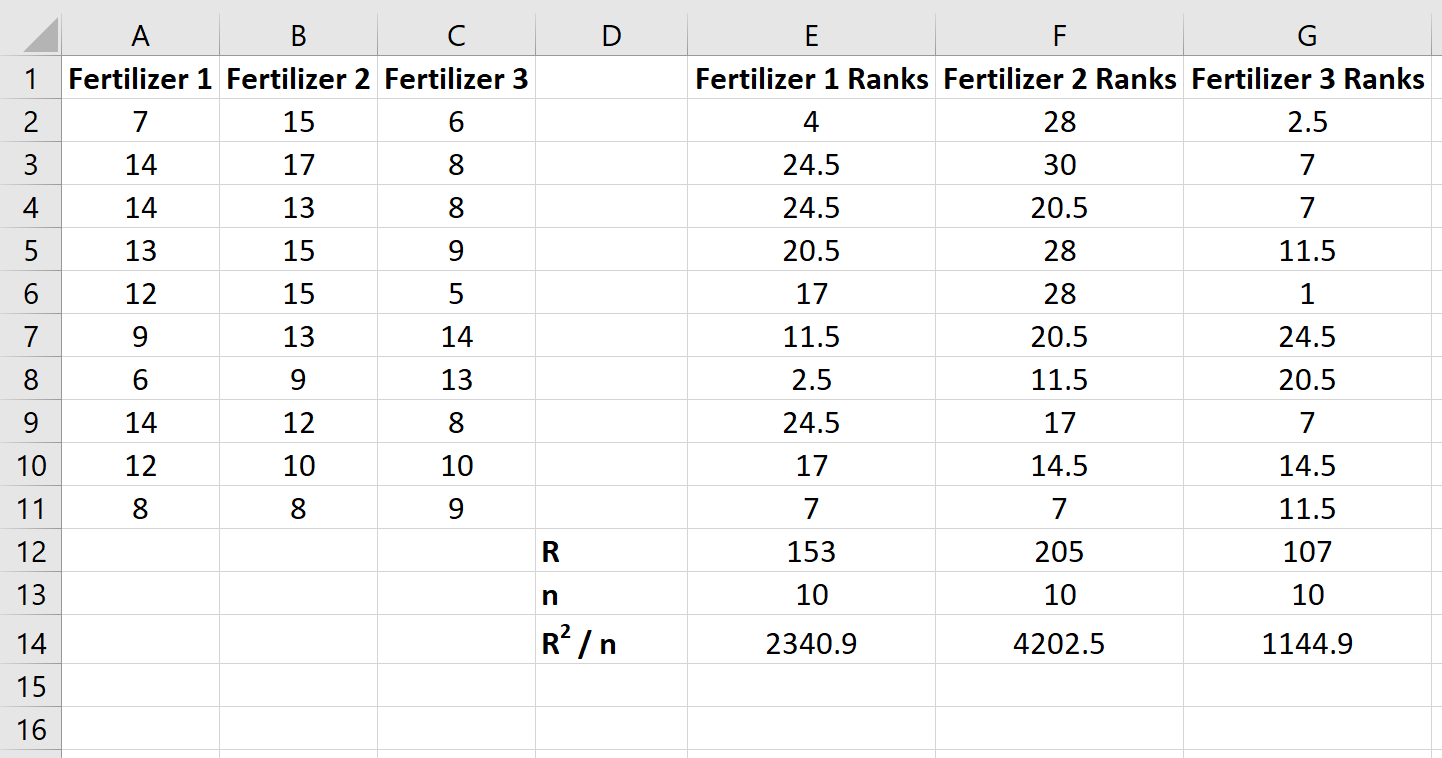
Шаг 3: Рассчитайте тестовую статистику и соответствующее значение p.
Статистика теста определяется как:
H = 12/(n(n+1)) * ΣR j 2 /n j – 3(n+1)
Золото:
- n = общий размер выборки
- R j 2 = сумма рангов j-й группы
- n j = размер выборки j-й группы
Согласно нулевой гипотезе, H следует распределению Хи-квадрат с k-1 степенями свободы.
На следующем снимке экрана показаны формулы, используемые для расчета статистики теста H и соответствующего значения p:
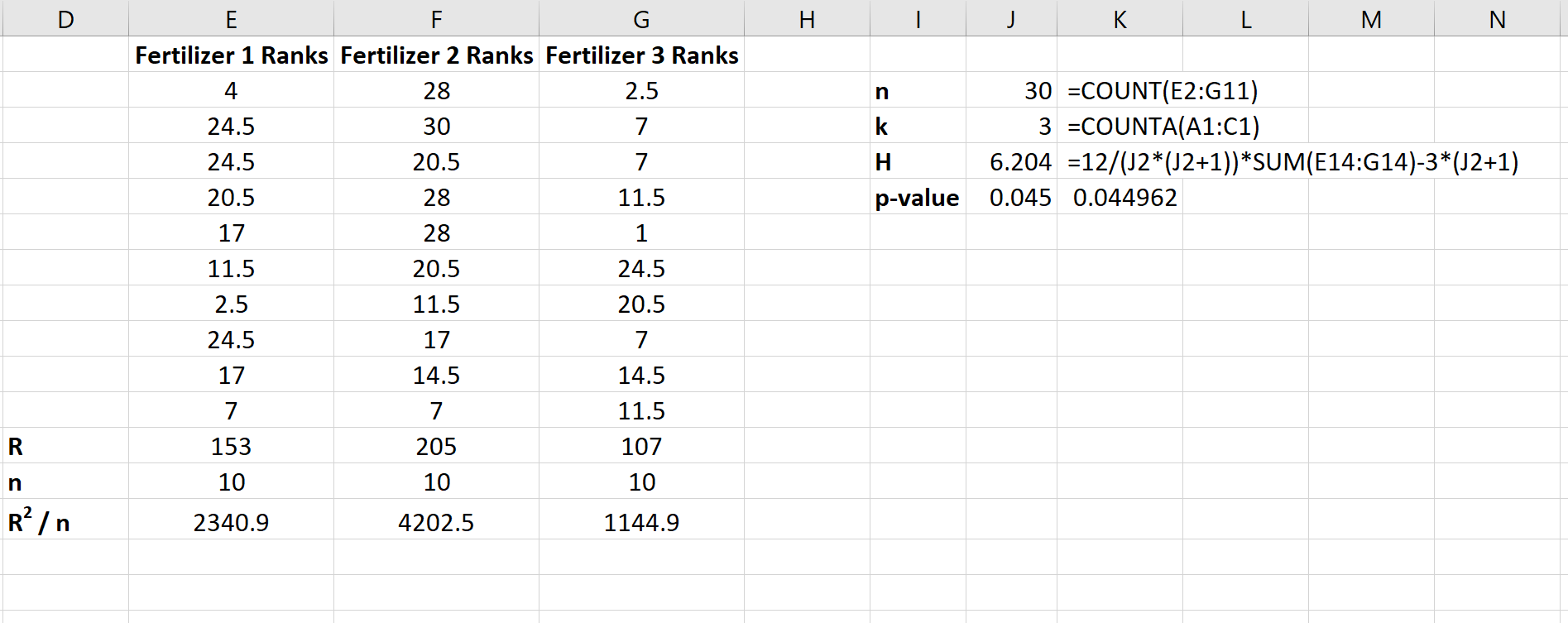
Статистика теста равна H = 6,204 , а соответствующее значение p — p = 0,045 . Поскольку это значение p меньше 0,05, мы можем отвергнуть нулевую гипотезу о том, что средний рост растений одинаков для всех трех удобрений. У нас есть достаточно доказательств, чтобы сделать вывод, что тип используемого удобрения вызывает статистически значимые различия в росте растений.
Шаг 4: Сообщите о результатах.
Наконец, мы хотели бы сообщить о результатах теста Крускала-Уоллиса. Вот пример того, как это сделать:
Был проведен тест Крускала-Уоллиста, чтобы определить, был ли средний рост растений одинаковым для трех разных удобрений для растений. Всего в анализе было использовано 30 растений. Каждое удобрение вносилось на 10 разных растений.
Тест показал, что средний рост растений не был одинаковым (H = 6,204, p = 0,045) между тремя удобрениями. То есть существовала статистически значимая разница в среднем росте растений при использовании двух или более удобрений.