Как выполнить тест крускала-уоллиса в sas

Тест Крускала-Уоллиса используется для определения наличия или отсутствия статистически значимой разницы между медианами трех или более независимых групп.

Он считается непараметрическим эквивалентом однофакторного дисперсионного анализа .

В этом руководстве представлен пошаговый пример выполнения теста Крускала-Уоллиса в SAS.

Шаг 1: Введите данные

Предположим, исследователи хотят знать, приводят ли три разных удобрения к разным уровням роста растений.

Они случайным образом выбирают 30 разных растений и делят их на три группы по 10, применяя к каждой группе разные удобрения. Через месяц измеряют высоту каждого растения.

Мы введем в SAS следующие данные, которые показывают общий рост (в дюймах) каждого из 10 растений в каждой группе:

 /*create dataset*/
data fertilizer_data;
    input fertilizer $growth;
    datalines ;
fert1 7
fert1 14
fert1 14
fert1 13
fert1 12
fert1 9
fert1 6
fert1 14
fert1 12
fert1 8
fert2 15
fert2 17
fert2 13
fert2 15
fert2 15
fert2 13
fert2 9
fert2 12
fert2 10
fert2 8
fert3 6
fert3 8
fert3 8
fert3 9
fert3 5
fert3 14
fert3 13
fert3 8
fert3 10
fert3 9
;
run ;

Шаг 2. Выполните тест Краскела-Уоллиса.

Далее мы воспользуемся оператором proc npar1way , чтобы выполнить тест Крускала-Уоллиса и сравнить средний рост растений между тремя группами удобрений:

 /*perform Kruskal-Wallis test*/
proc npar1way data =fertilizer_data wilcoxon dscf ;
    class fertilizer;
    vargrowth ;
run ;

Шаг 3: Интерпретируйте результаты

Первая таблица результатов показывает общую статистику теста Хи-квадрат и соответствующее значение p для теста Крускала-Уоллиса:

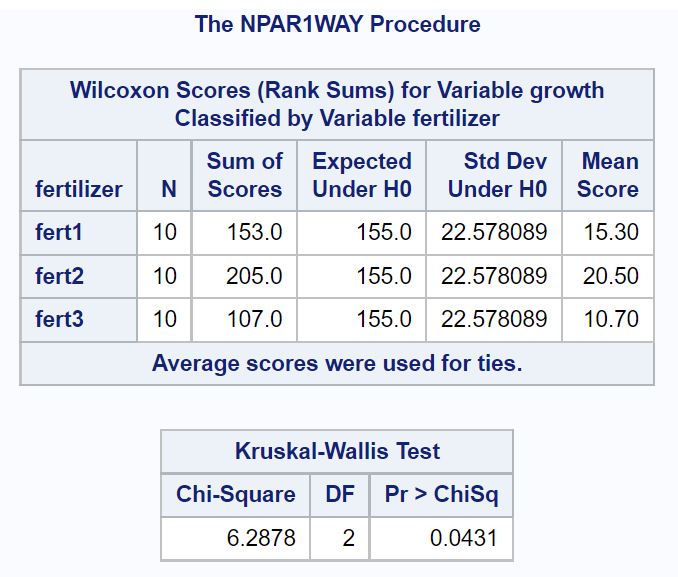
P-значение теста составляет 0,0431 . Поскольку это значение меньше 0,05, мы отвергаем нулевую гипотезу о том, что средний рост растений одинаков для всех трех удобрений.

Это означает, что у нас есть достаточно доказательств, чтобы сделать вывод, что тип используемого удобрения вызывает статистически значимые различия в росте растений.

В итоговой таблице результатов показаны значения p для парных сравнений между каждой из трех групп:

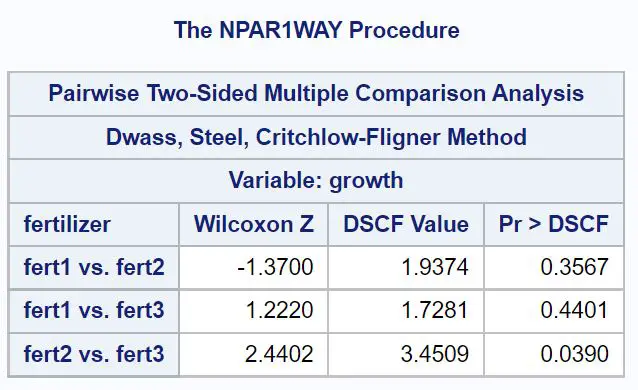
Из этой таблицы мы видим, что единственное значение p ниже 0,05 — это сравнение между удобрением 2 и удобрением 3, значение p которого равно 0,0390 .

Это означает, что существует статистически значимая разница в росте растений между удобрением 2 и удобрением 3, но не между другими парными сравнениями.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные статистические тесты в SAS:

Как выполнить одновыборочный t-тест в SAS
Как выполнить t-тест с двумя выборками в SAS
Как выполнить односторонний дисперсионный анализ в SAS
Как выполнить двусторонний дисперсионный анализ в SAS