Как выполнить тест крускала-уоллиса в spss

Тест Крускала -Уоллиса используется для определения наличия или отсутствия статистически значимой разницы между медианами трех или более независимых групп. Он считается непараметрическим эквивалентом однофакторного дисперсионного анализа .

В этом руководстве объясняется, как выполнить тест Крускала-Уоллиса в SPSS.

Пример: тест Крускала-Уоллиса в SPSS

Исследователь хочет знать, оказывают ли три лекарства различное воздействие на боль в колене. Поэтому он набирает 30 человек, которые испытывают одинаковую боль в коленях, и случайным образом делит их на три группы, которые получают либо препарат 1, либо препарат 2, либо препарат 3.

После месяца приема препарата исследователь просит каждого человека оценить боль в колене по шкале от 1 до 100, где 100 указывает на самую сильную боль. Результаты 30 человек представлены ниже:

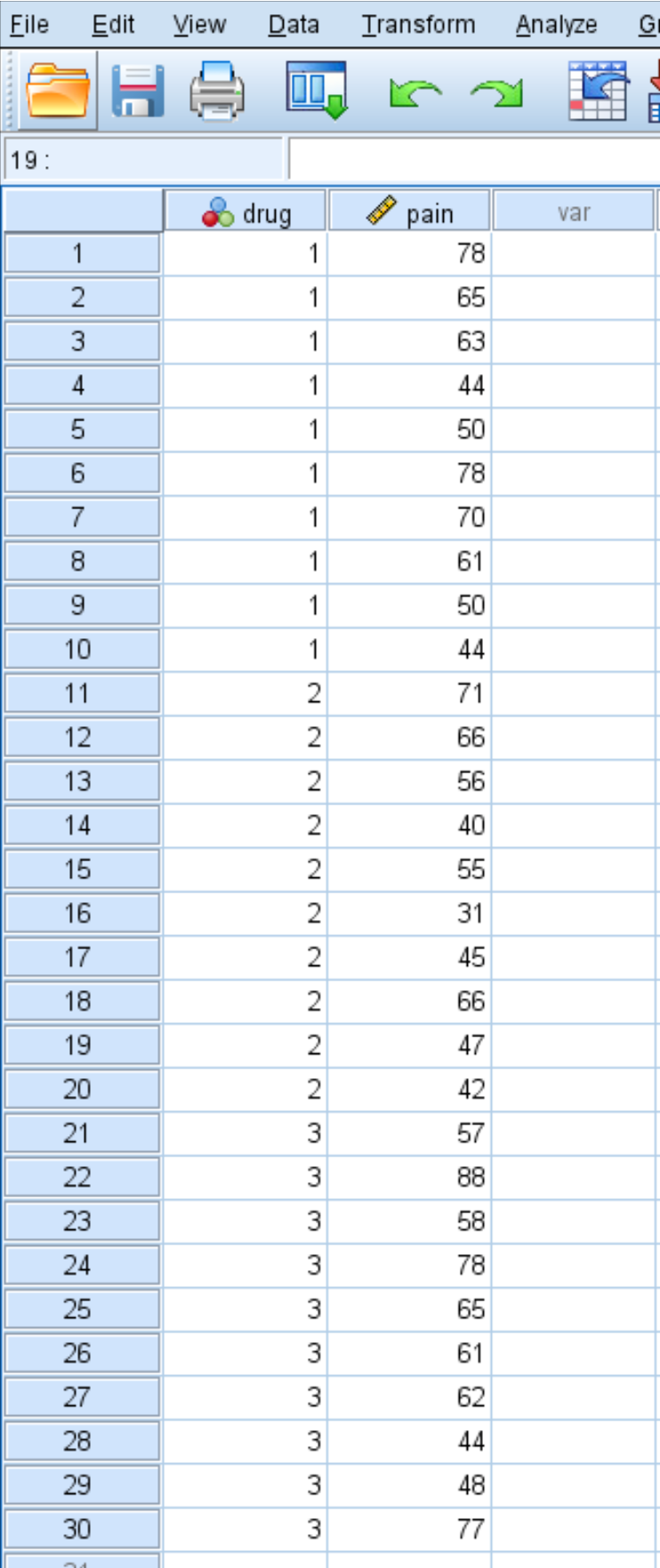
Выполните следующие шаги, чтобы выполнить тест Крускала-Уоллиса, чтобы определить, существует ли разница в зарегистрированных уровнях боли в колене между тремя группами:

Шаг 1: Выполните тест Крускала-Уоллиса.

Перейдите на вкладку «Анализ» , затем «Непараметрические критерии» , затем «Устаревшие диалоги» , затем «K независимых выборок »:

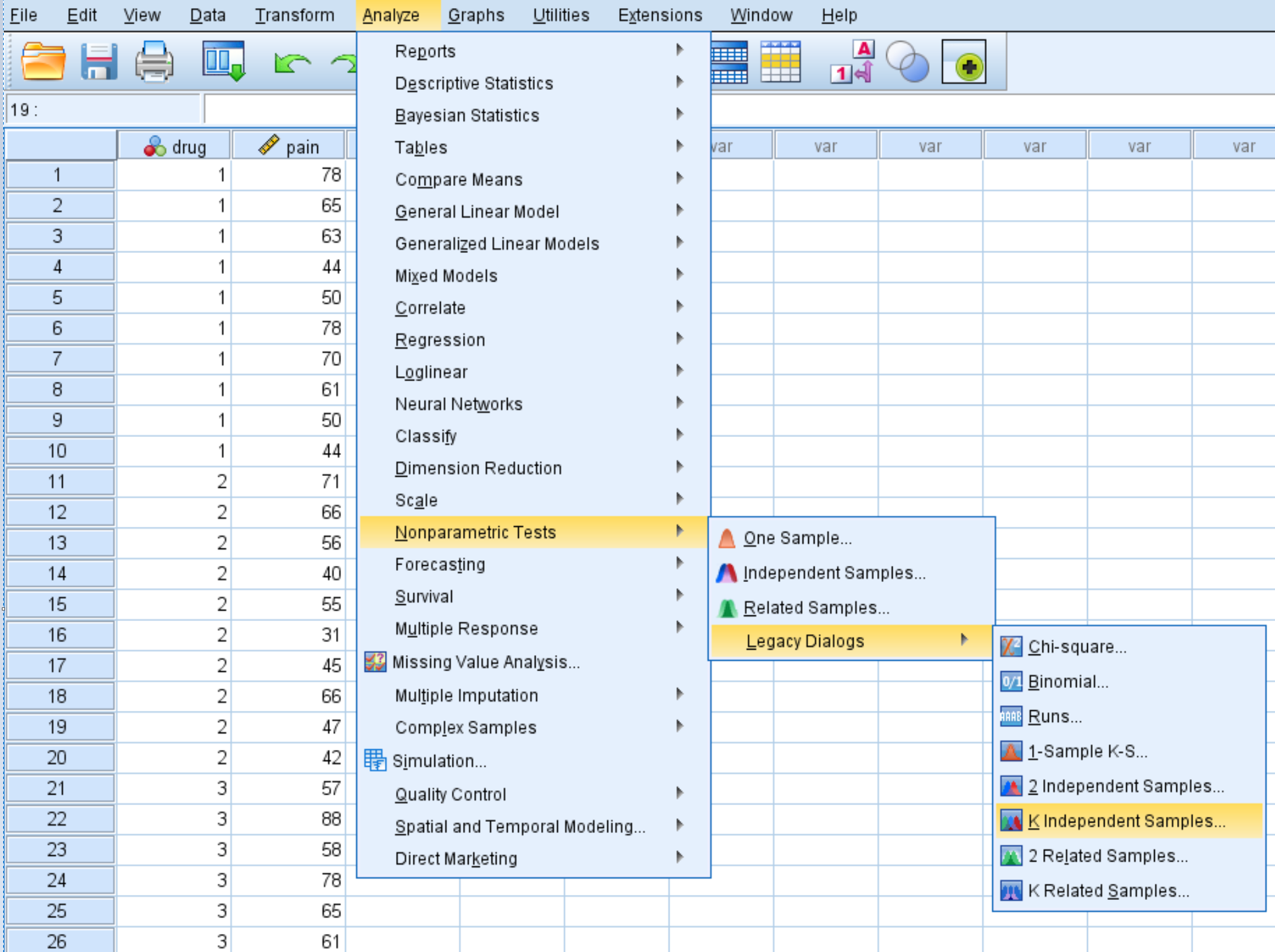
В появившемся окне перетащите переменную боли в поле «Список тестовых переменных», а «Лекарство» — в поле «Группирующая переменная». Затем нажмите «Установить диапазон» и установите минимальное значение 1 и максимальное значение 3. Затем нажмите «Продолжить» . Убедитесь, что флажок рядом с Kruskal-Wallis H установлен, затем нажмите «ОК» .

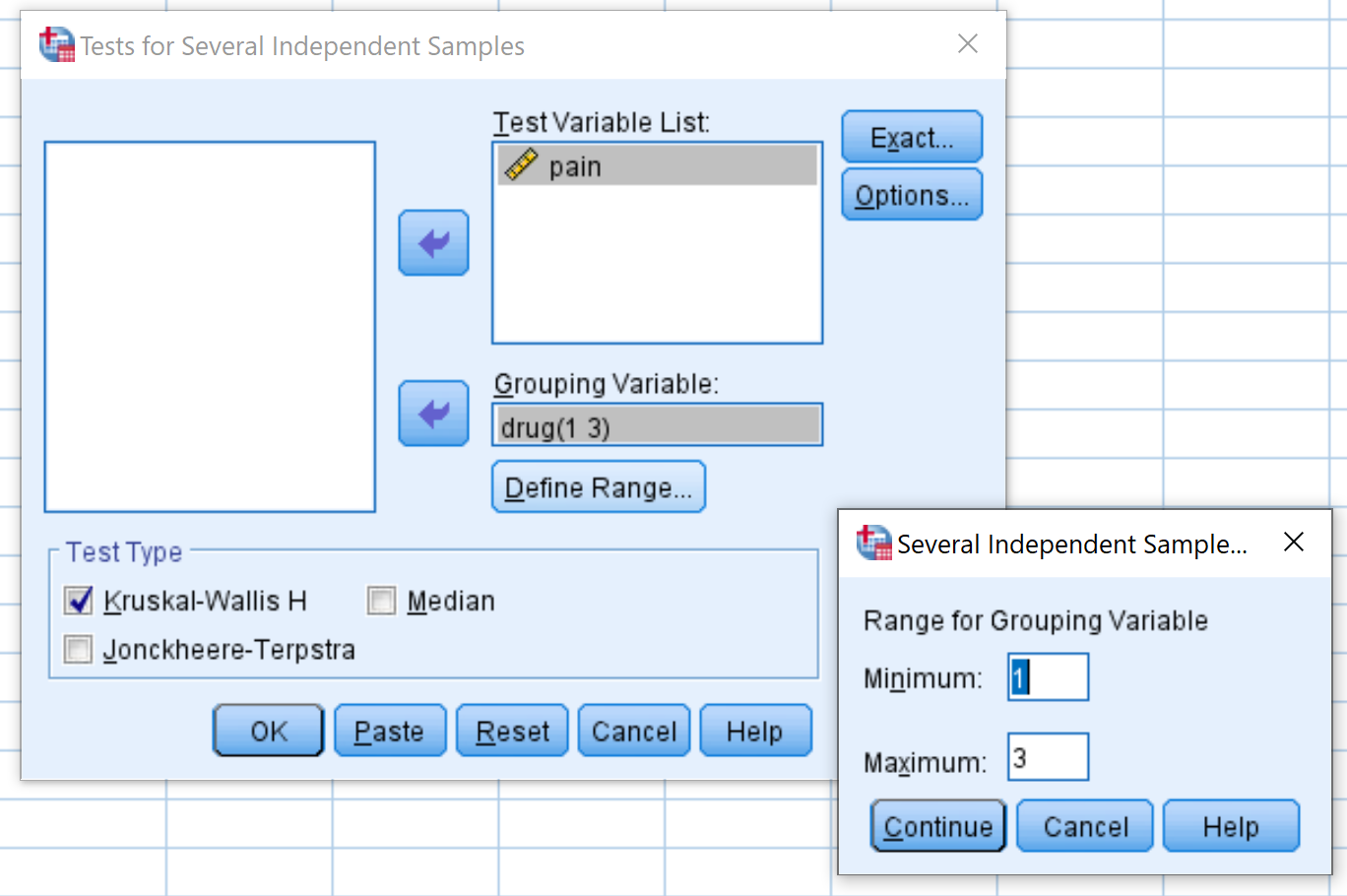
Шаг 2: Интерпретируйте результаты.

Как только вы нажмете «ОК» , появятся результаты теста Крускала-Уоллиса:

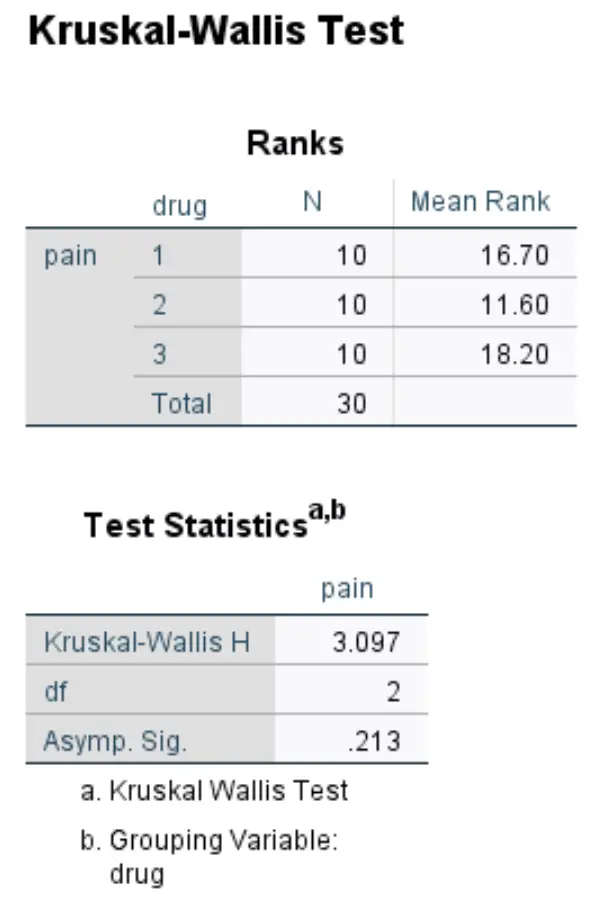
Вторая таблица вывода отображает результаты теста:

• Краскал-Уоллис Х: Это статистика теста X ² .
• df: Это степени свободы, рассчитанные как #groups-1 = 3-1 = 2.
• Асимп. Sig: Это значение p, связанное со статистикой теста X ² 3,097 с 2 степенями свободы. Это также можно найти с помощью калькулятора преобразования хи-квадрат в P-значение.

Поскольку значение p (0,213) не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что существует статистически значимая разница в оценке боли в коленях между этими тремя группами.