Как выполнить тест чоу в r
Тест Чоу используется для проверки того, равны ли коэффициенты двух разных моделей регрессии в разных наборах данных.
Этот тест обычно используется в области эконометрики с данными временных рядов, чтобы определить, есть ли структурный разрыв в данных в данный момент времени.
В этом руководстве представлен пошаговый пример выполнения теста Чоу в R.
Шаг 1. Создайте данные
Сначала мы создадим поддельные данные:
#create data data <- data.frame(x = c(1, 1, 2, 3, 4, 4, 5, 5, 6, 7, 7, 8, 8, 9, 10, 10, 11, 12, 12, 13, 14, 15, 15, 16, 17, 18, 18, 19, 20, 20), y = c(3, 5, 6, 10, 13, 15, 17, 14, 20, 23, 25, 27, 30, 30, 31, 33, 32, 32, 30, 32, 34, 34, 37, 35, 34, 36, 34, 37, 38, 36)) #view first six rows of data head(data) xy 1 1 3 2 1 5 3 2 6 4 3 10 5 4 13 6 4 15
Шаг 2. Визуализируйте данные
Далее мы создадим простую диаграмму рассеяния для визуализации данных:
#load ggplot2 visualization package library (ggplot2) #create scatterplot ggplot(data, aes (x = x, y = y)) + geom_point(col=' steelblue ', size= 3 )
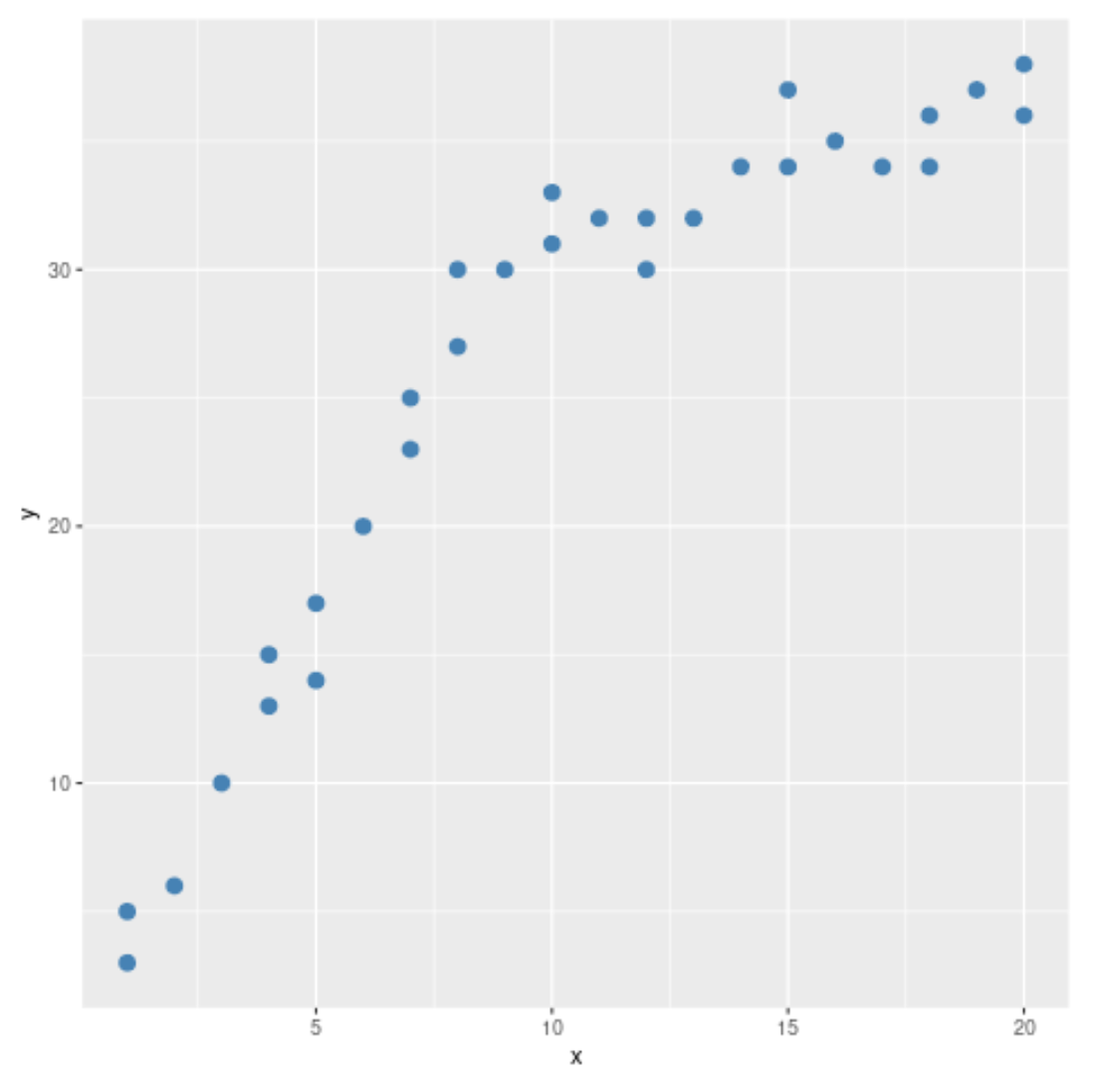
Из диаграммы рассеяния мы видим, что картина в данных меняется при x = 10. Таким образом, мы можем выполнить тест Чоу, чтобы определить, есть ли точка структурного разрыва в данных при x = 10.
Шаг 3: Проведите тест чау
Мы можем использовать функцию sctest из пакета strucchange для выполнения теста Чоу:
#load strucchange package library (strucchange) #perform Chow test sctest(data$y ~ data$x, type = " Chow ", point = 10 ) Chow test data: data$y ~ data$x F = 110.14, p-value = 2.023e-13
По результатам теста мы видим:
- Статистика F-теста : 110,14
- p-значение: <.0000
Поскольку значение p меньше 0,05, мы можем отвергнуть нулевую гипотезу теста. Это означает, что у нас есть достаточно доказательств, чтобы сказать, что в данных присутствует структурная точка излома.
Другими словами, две линии регрессии могут более эффективно соответствовать модели данным, чем одна линия регрессии.