Как выполнить знаковый ранговый тест уилкоксона в sas
Критерий знакового ранга Уилкоксона — это непараметрическая версия t-критерия для парных выборок .
Он используется для проверки того, существует ли значительная разница между средними значениями двух популяций, когда распределение различий между двумя выборками нельзя считать нормальным.
В следующем примере показано, как выполнить тест знакового ранга Уилкоксона в SAS.
Пример: тест ранга, подписанный Уилкоксоном, в SAS.
Предположим, инженер хочет знать, приводит ли новая обработка топлива к изменению среднего пробега на галлон определенного автомобиля. Чтобы проверить это, он измеряет расход миль на галлон у 12 автомобилей с обработкой топлива и без нее.
Результаты представлены в таблице ниже:
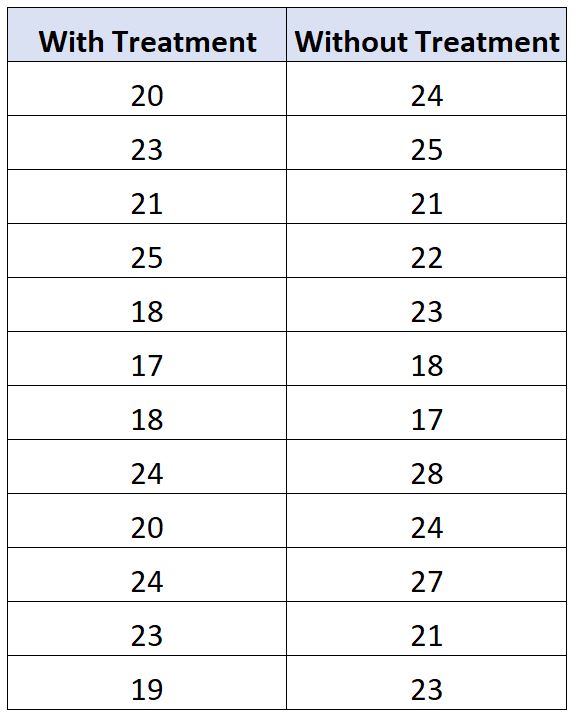
Мы можем использовать следующий код для выполнения теста знакового ранга Уилкоксона в SAS, чтобы определить, существует ли значительная разница в среднем расходе миль на галлон между двумя группами:
/*create dataset*/ data my_data; input car with_fuel without_fuel; datalines ; 1 20 24 2 23 25 3 21 21 4 25 22 5 18 23 6 17 18 7 18 17 8 24 28 9 20 24 10 24 27 11 23 21 12 19 23 ; run ; /*create new dataset with difference between two fuel treatments*/ data my_data2; set my_data; diff=with_fuel-without_fuel; run ; /*perform Wilcoxon Signed Rank Test*/ proc univariate data=my_data2; var diff; run ;
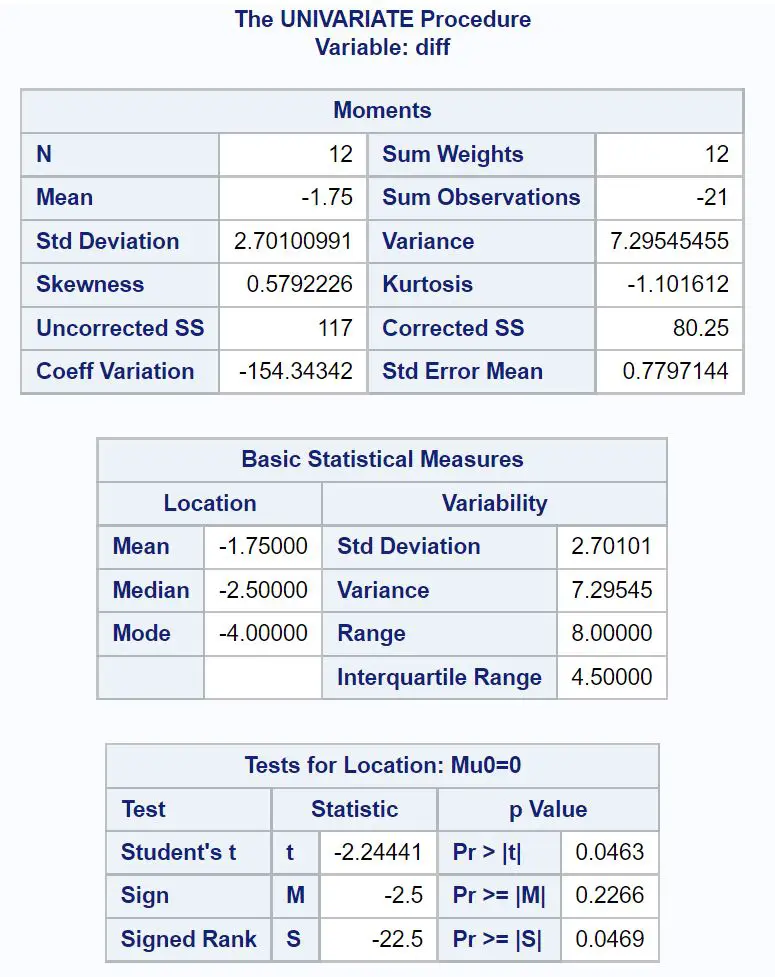
Из результатов мы видим, что средняя разница в расходе миль на галлон между автомобилями, прошедшими обработку, и теми, которые этого не сделали, составляет -1,75 .
В таблице « Тесты местоположения» мы можем наблюдать следующее:
- Статистика рангового теста Уилкоксона: -22,5.
- Соответствующее значение p: 0,0469.
Напомним, что критерий знакового ранга Уилкоксона использует следующие нулевые и альтернативные гипотезы:
- H 0 : MPG одинаков между двумя группами.
- H A : MPG не одинаков между двумя группами.
Поскольку значение p теста (0,0469) меньше 0,05, мы отвергаем нулевую гипотезу.
Это означает, что у нас есть достаточно доказательств, чтобы сказать, что средний расход миль на галлон не равен между двумя группами.