Как проверить нормальность в r (4 метода)

Многие статистические тесты предполагают , что наборы данных распределены нормально.

Есть четыре распространенных способа проверить это предположение в R:

1. (Визуальный метод) Создайте гистограмму.

• Если гистограмма имеет приблизительно форму «колокола», то предполагается, что данные распределены нормально.

2. (Визуальный метод) Создайте график QQ.

• Если точки на графике лежат примерно вдоль прямой диагональной линии, то предполагается, что данные распределены нормально.

3. (Формальный статистический тест) Выполните тест Шапиро-Уилка.

• Если значение p теста больше α = 0,05, то предполагается, что данные распределены нормально.

4. (Формальный статистический тест) Выполните тест Колмогорова-Смирнова.

• Если значение p теста больше α = 0,05, то предполагается, что данные распределены нормально.

Следующие примеры показывают, как использовать каждый из этих методов на практике.

Метод 1: создайте гистограмму

Следующий код показывает, как создать гистограмму для нормально распределенного и ненормально распределенного набора данных в R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

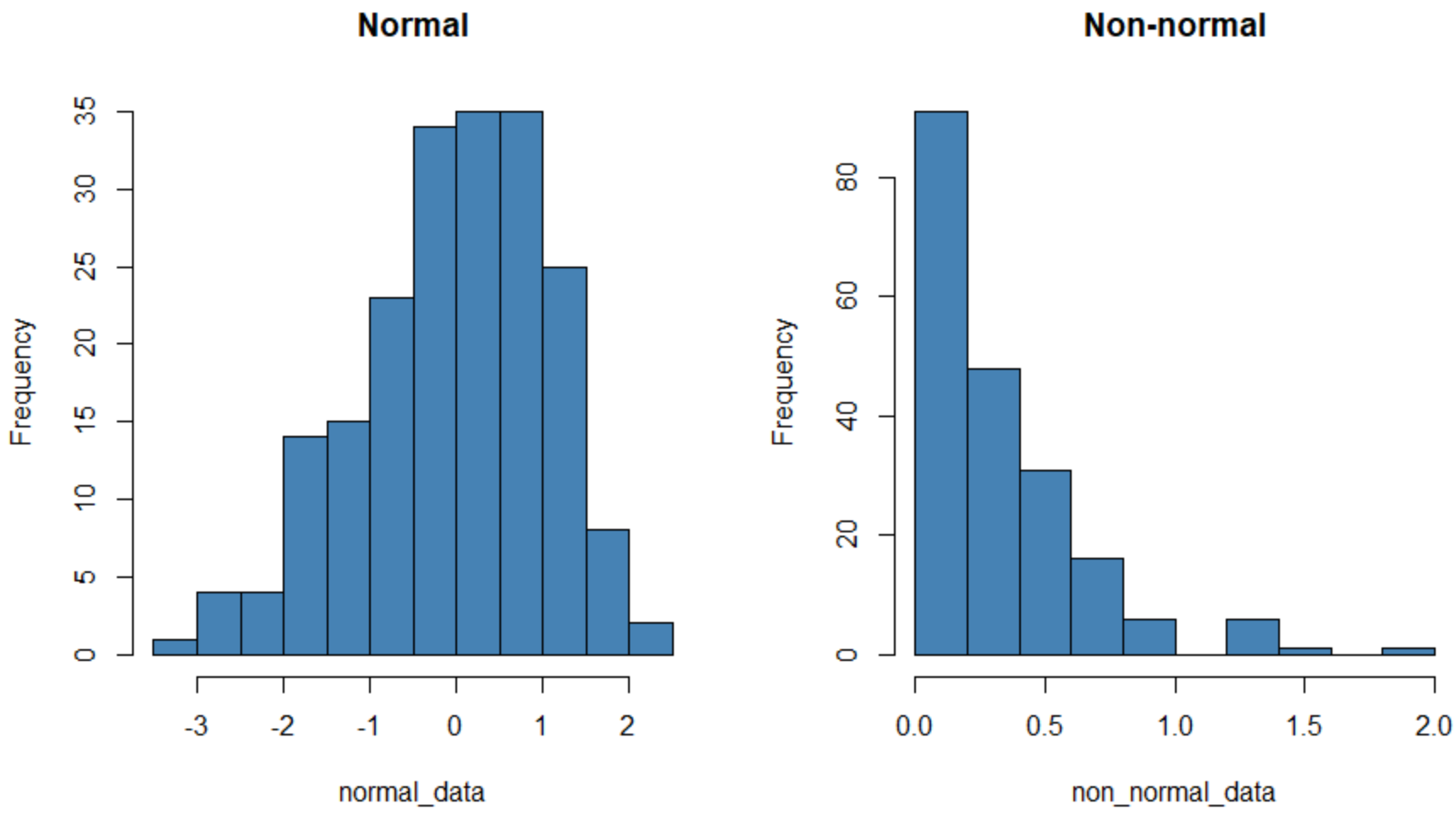
Гистограмма слева показывает набор данных, который имеет нормальное распределение (примерно в форме колокола), а гистограмма справа показывает набор данных, который не имеет нормального распределения.

Метод 2: Создайте график QQ

Следующий код показывает, как создать график QQ для нормально распределенного и ненормально распределенного набора данных в R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

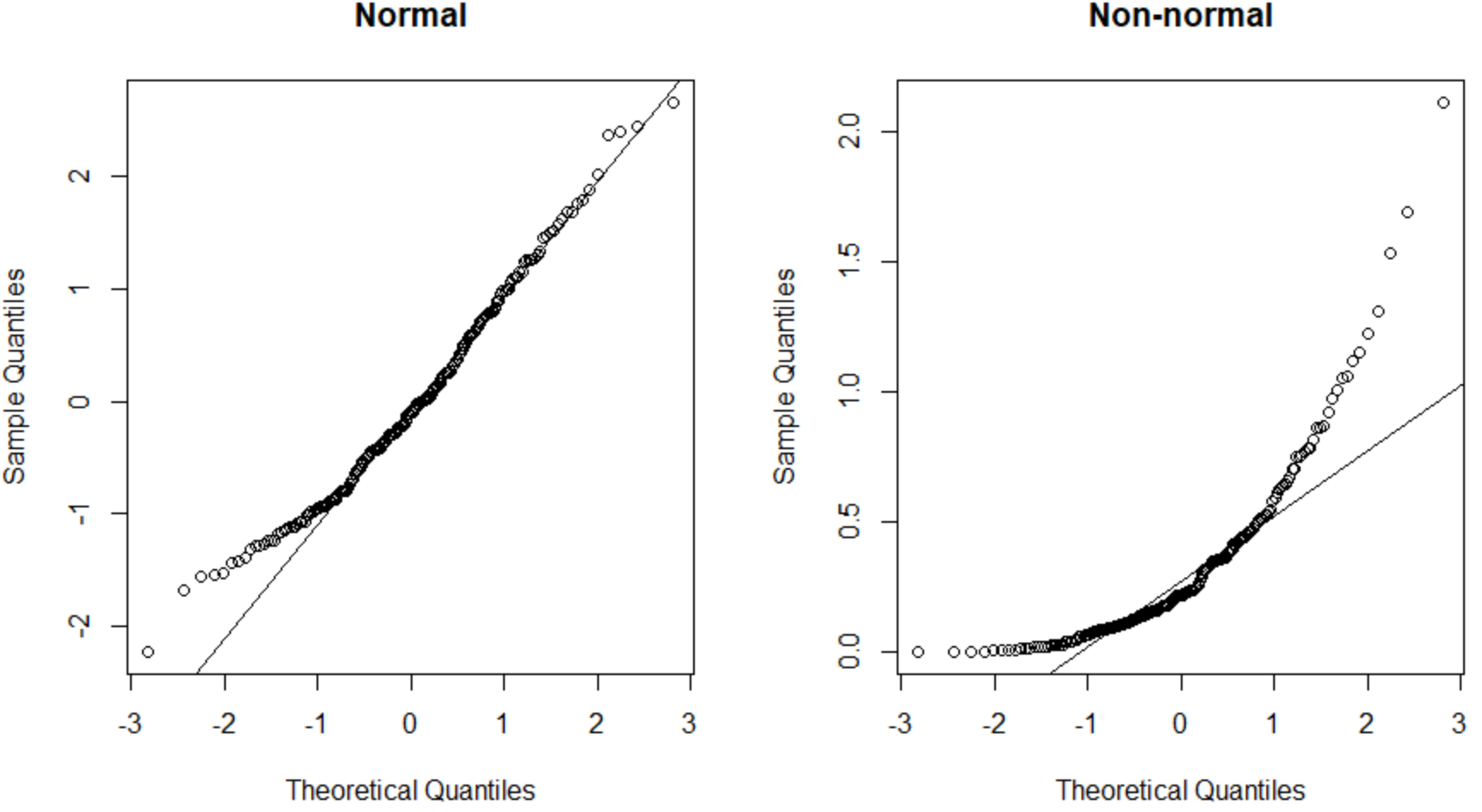
График QQ слева представляет набор данных с нормальным распределением (точки располагаются вдоль прямой диагональной линии), а график QQ справа представляет набор данных с ненормальным распределением.

Метод 3. Проведите тест Шапиро-Уилка.

Следующий код показывает, как выполнить тест Шапиро-Уилка для нормально распределенного и ненормально распределенного набора данных в R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

Значение p первого теста составляет не менее 0,05, что указывает на нормальное распределение данных.

Значение p второго теста меньше 0,05, что указывает на то, что данные не распределены нормально.

Метод 4: выполнить тест Колмогорова-Смирнова.

Следующий код показывает, как выполнить тест Колмогорова-Смирнова для нормально распределенного и ненормально распределенного набора данных в R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

Значение p первого теста составляет не менее 0,05, что указывает на нормальное распределение данных.

Значение p второго теста меньше 0,05, что указывает на то, что данные не распределены нормально.

Как обрабатывать нестандартные данные

Если данный набор данных не является нормально распределенным, мы часто можем выполнить одно из следующих преобразований, чтобы сделать его более нормально распределенным:

1. Преобразование журнала: преобразуйте значения x в log(x) .

2. Преобразование квадратного корня: преобразуйте значения x в √x .

3. Преобразование корня куба: преобразуйте значения x в x ^1/3 .

Выполняя эти преобразования, набор данных обычно становится более нормально распределенным.

Прочтите это руководство , чтобы узнать, как выполнить эти преобразования в R.

Дополнительные ресурсы

Как создавать гистограммы в R
Как создать и интерпретировать график QQ в R
Как выполнить тест Шапиро-Уилка в R
Как выполнить тест Колмогорова-Смирнова в R