Как выполнить тест независимости хи-квадрат в spss
Критерий независимости хи-квадрат используется для определения наличия значимой связи между двумя категориальными переменными.
В этом руководстве объясняется, как выполнить проверку независимости по хи-квадрату в SPSS.
Пример: тест независимости хи-квадрат в SPSS
Предположим, мы хотим знать, связан ли пол с предпочтением той или иной политической партии. Мы берем простую случайную выборку из 500 избирателей и спрашиваем их об их предпочтениях в отношении политических партий. В следующей таблице представлены результаты опроса:
| республиканец | Демократ | Независимый | Общий | |
| Мужской | 120 | 90 | 40 | 250 |
| Женский | 110 | 95 | 45 | 250 |
| Общий | 230 | 185 | 85 | 500 |
Используйте следующие шаги, чтобы выполнить тест независимости хи-квадрат в SPSS, чтобы определить, связан ли пол с предпочтениями политической партии.
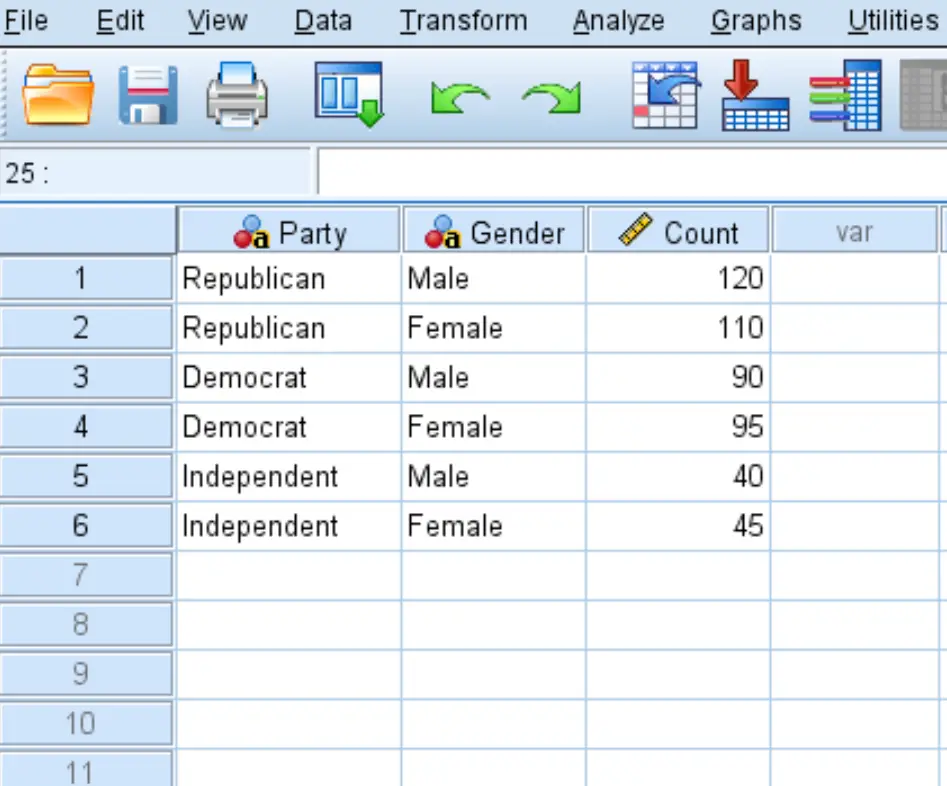
Шаг 1: Введите данные.
Сначала введите данные в следующем формате:
Шаг 2: Используйте утяжеленные коробки.
Чтобы тест работал правильно, нам нужно сообщить SPSS, что переменные Party и Gender должны иметь вес по переменной Count.
Перейдите на вкладку «Данные» , затем нажмите «Весовые случаи» :
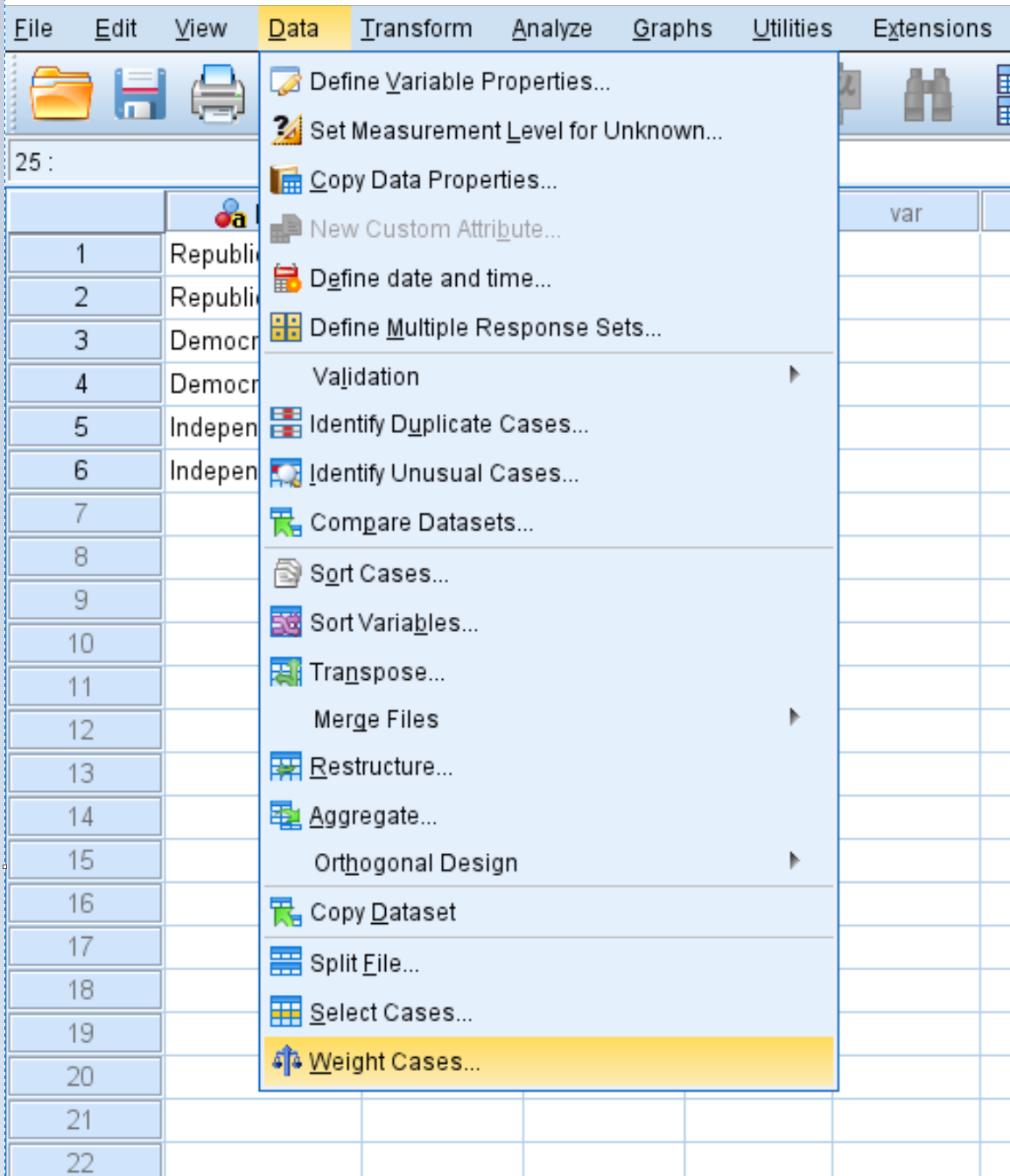
В появившемся новом окне перетащите переменную Count в область с надписью «Список тестовых переменных». Затем нажмите ОК .
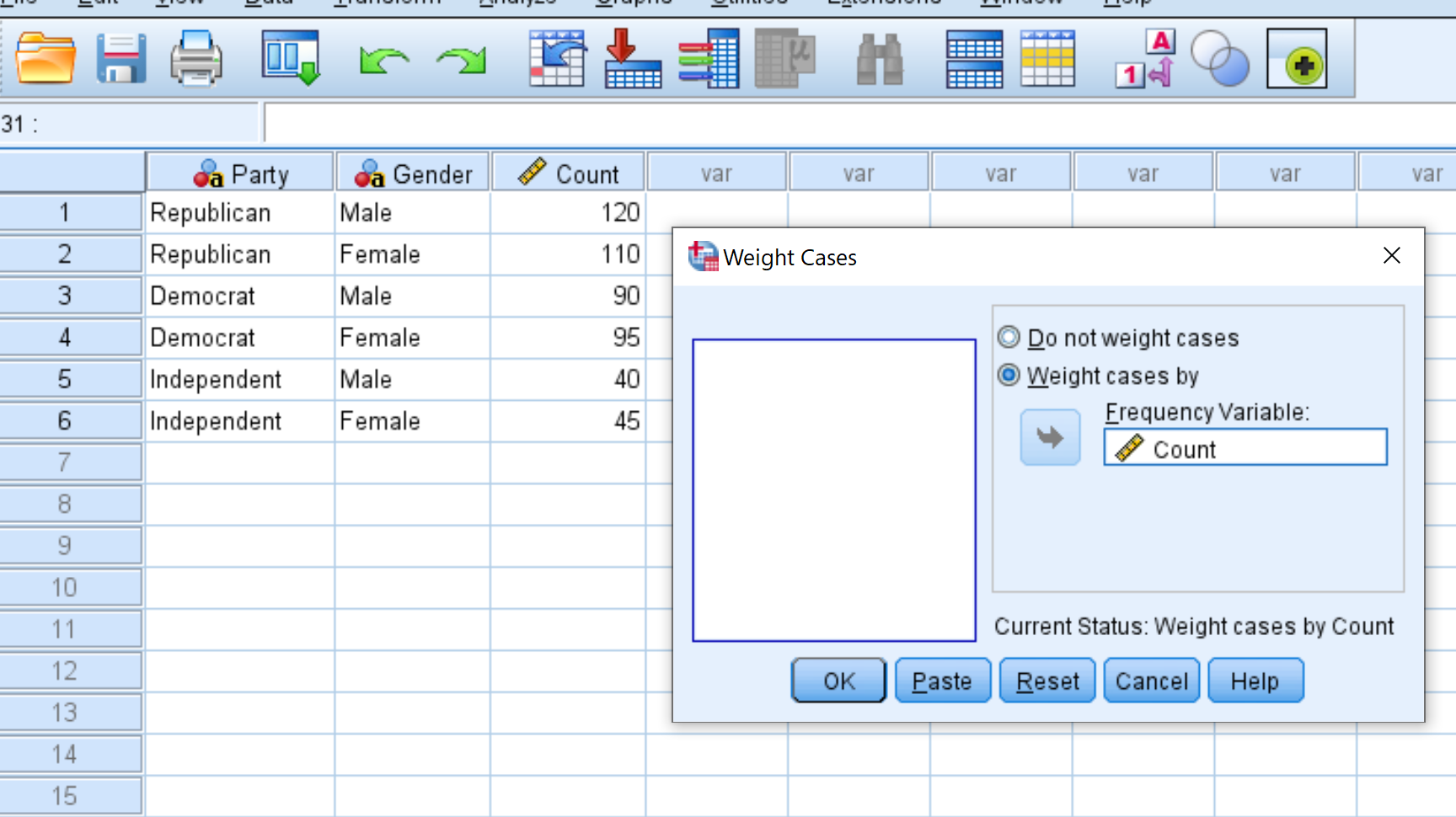
Шаг 3. Выполните критерий согласия хи-квадрат.
Перейдите на вкладку «Анализ» , затем «Описательная статистика» , затем «Кросс-таблицы» :
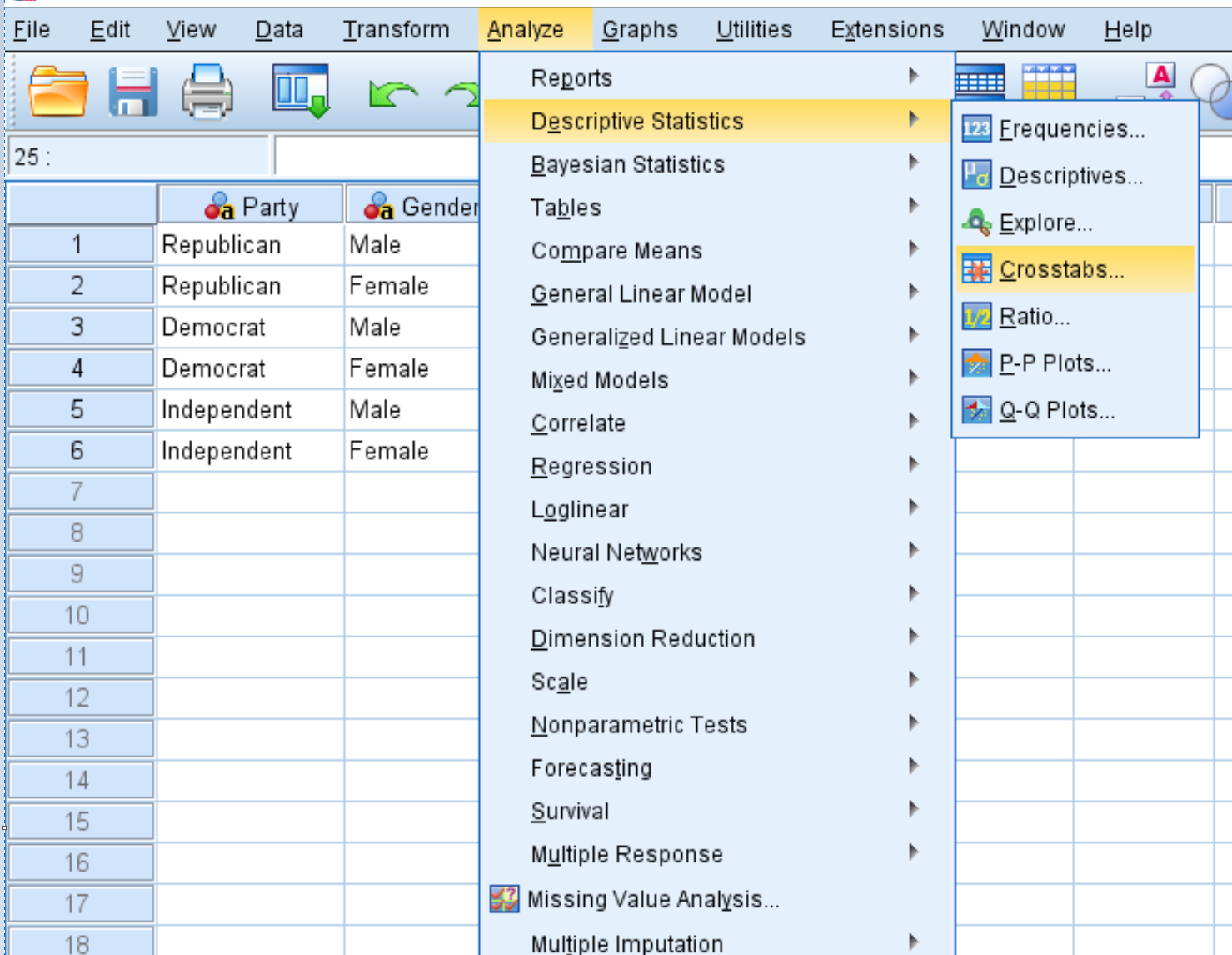
В появившемся новом окне перетащите переменную «Жанр» в область «Строки», а переменную « Часть» в область «Столбцы». Затем нажмите «Статистика» и убедитесь, что установлен флажок рядом с «Квадрат Чи» . Нажмите «Продолжить» . Затем нажмите ОК .
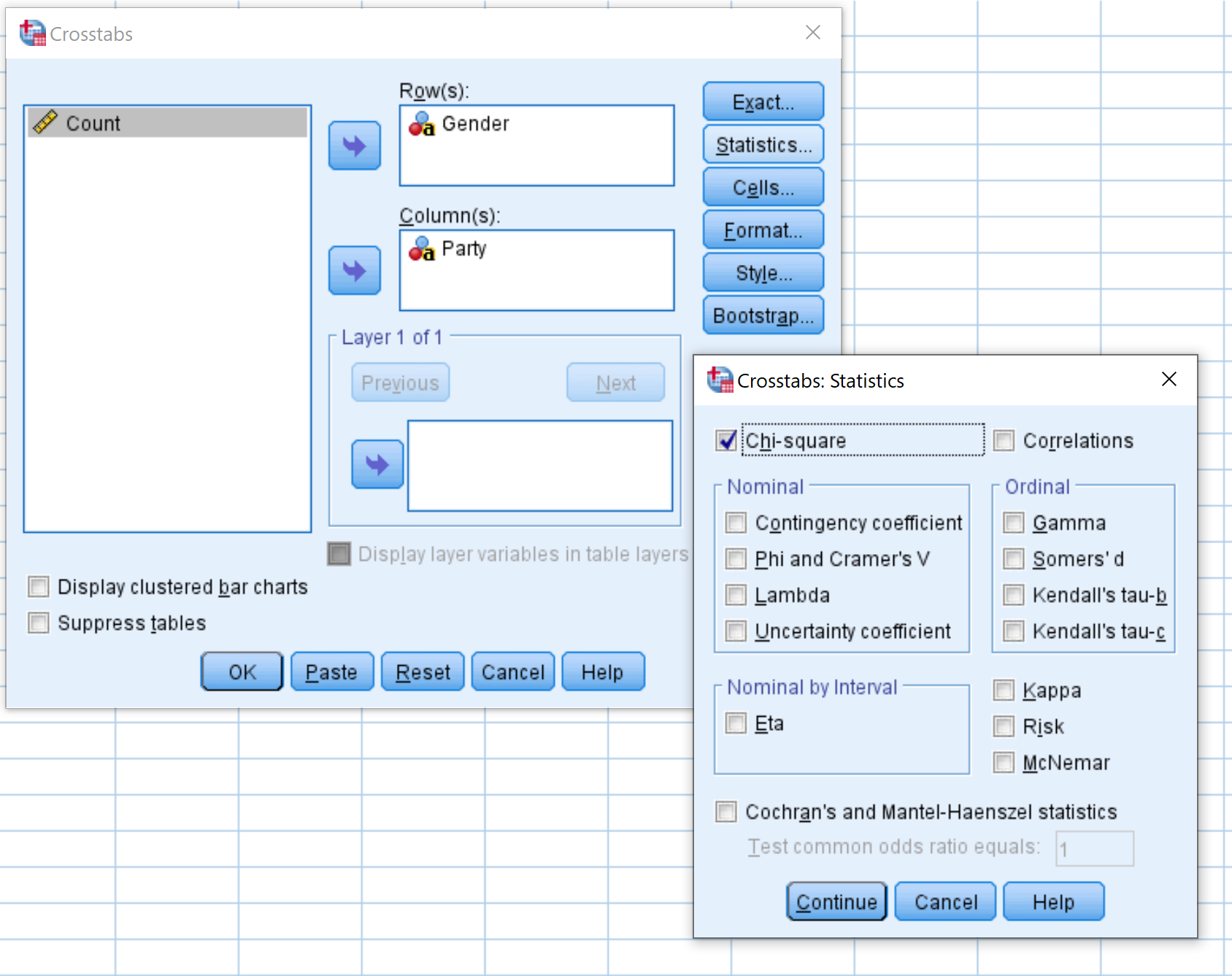
Шаг 4: Интерпретируйте результаты .
Как только вы нажмете «ОК» , появятся результаты теста независимости хи-квадрат:
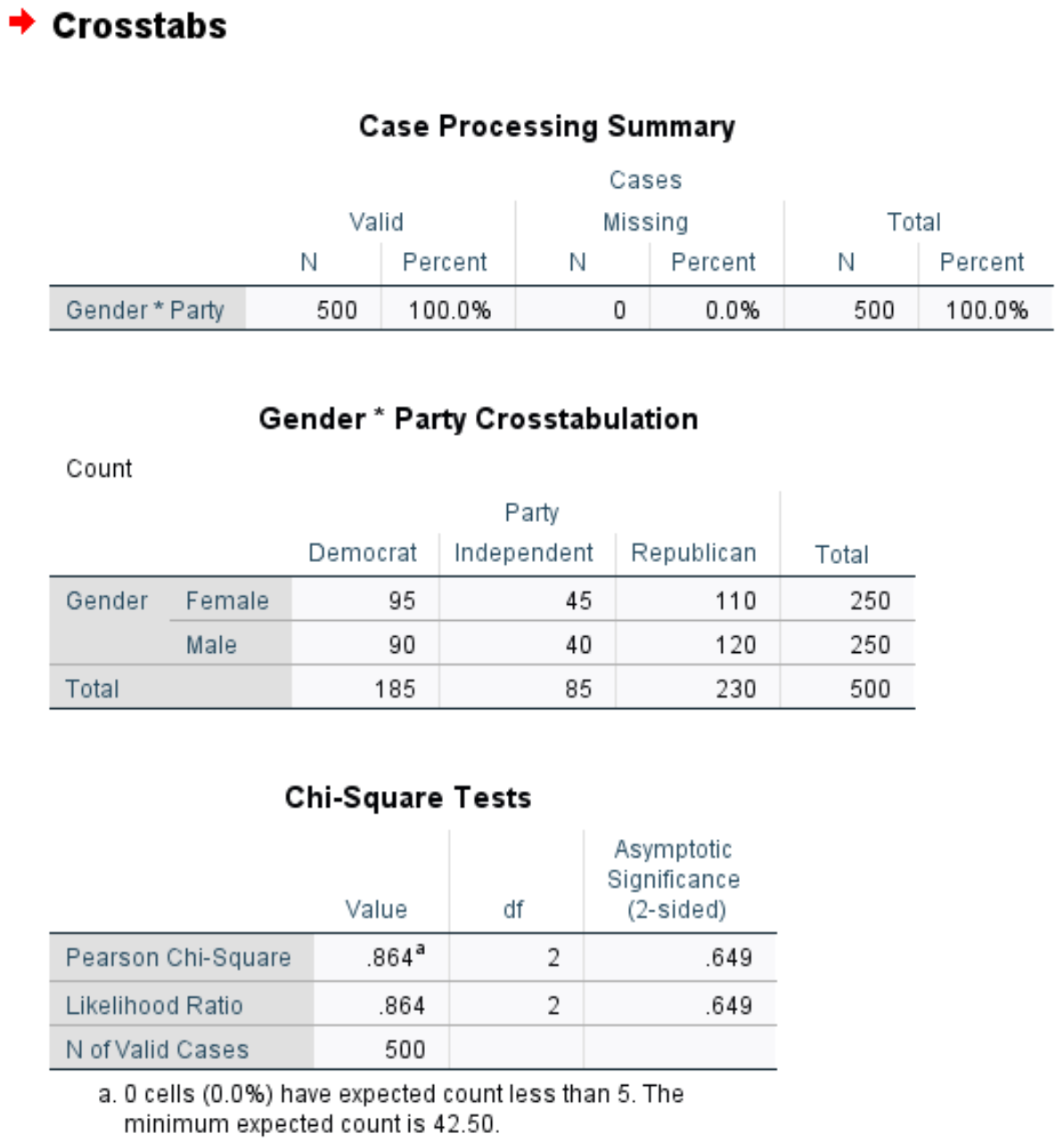
В первой таблице показано количество пропущенных случаев в наборе данных. Мы видим, что в этом примере 0 пропущенных случаев.
Во второй таблице представлена перекрестная таблица общего числа людей по полу и предпочтениям политических партий.
В третьей таблице показаны результаты теста независимости хи-квадрат. Статистика теста равна 0,864 , а соответствующее двустороннее значение p — 0,649 .
Нулевая гипотеза критерия независимости хи-квадрат состоит в том, что две переменные независимы. В этом случае наша нулевая гипотеза состоит в том, что предпочтения пола и политических партий независимы.
Поскольку значение p (0,649) теста не менее 0,05, мы не можем отвергнуть нулевую гипотезу.
Это означает, что у нас нет достаточных доказательств, чтобы утверждать, что существует связь между полом и предпочтениями политических партий.