Как выполнить t-тесты в google sheets
Вообще говоря, существует три типа t-тестов:
- Образец t-теста
- Двухвыборочный Т-тест
- Парные выборки t-критерий
В этом руководстве представлены примеры выполнения каждого из этих тестов в Google Sheets.
Пример: t-критерий для одной выборки
Определение: Одновыборочный t-критерий используется для проверки того, соответствует ли среднее значение совокупности определенному значению.
Пример: Ботаник хочет знать, равна ли средняя высота определенного вида растений 15 дюймам. Она берет случайную выборку из 12 растений и записывает высоту каждого из них в дюймах.
На следующем снимке экрана показано, как выполнить t-тест для одной выборки, чтобы определить, равен ли истинный средний рост населения 15 дюймам:
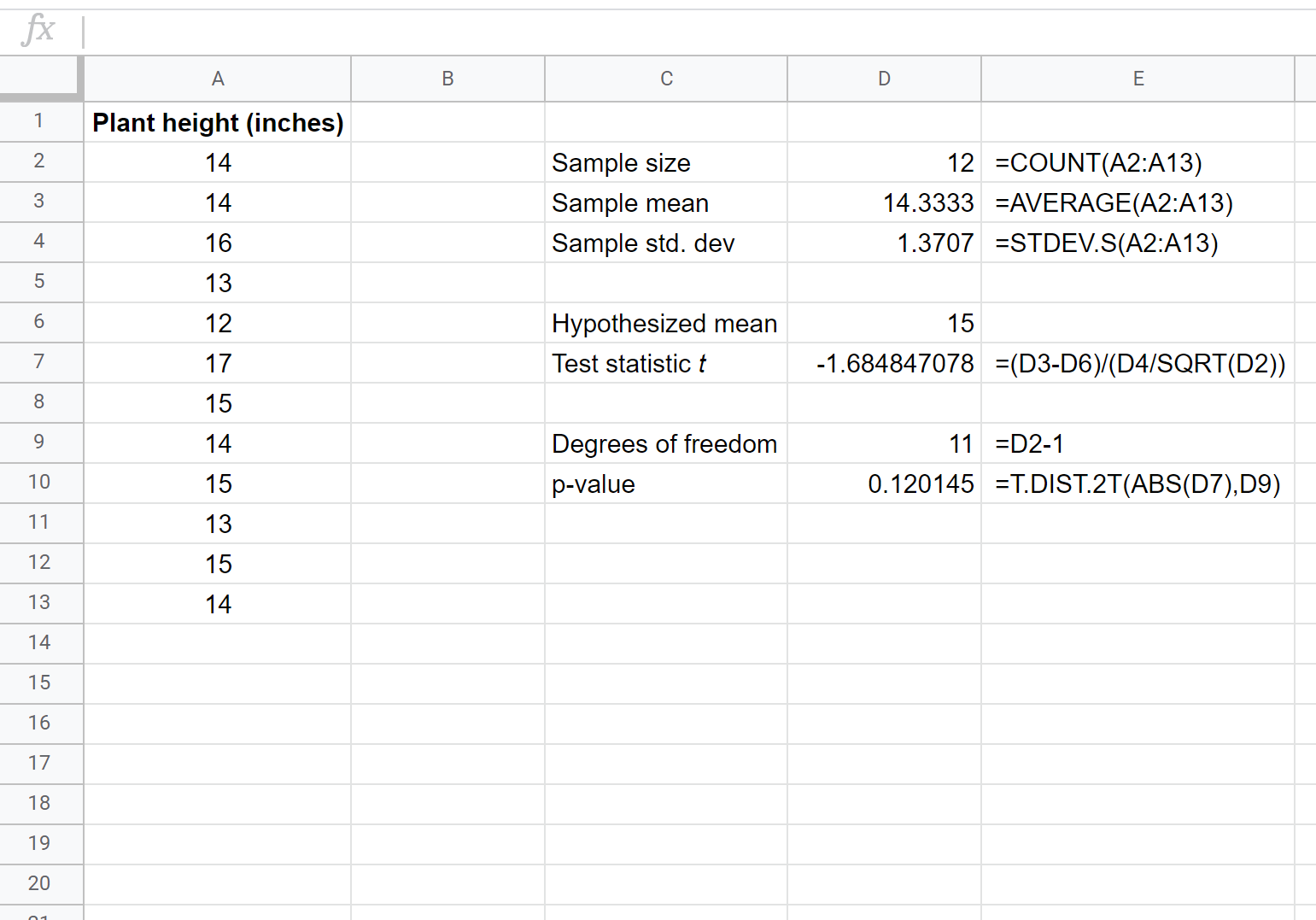
Две гипотезы для этого t-теста на конкретной выборке заключаются в следующем:
H 0 : µ = 15 (средняя высота этого вида растений 15 дюймов)
H A : µ ≠15 (средний рост не 15 дюймов)
Поскольку значение p нашего теста (0,120145) превышает альфа = 0,05, мы не можем отвергнуть нулевую гипотезу теста. У нас нет достаточных доказательств, чтобы сказать, что средняя высота этого конкретного вида растений составляет что-либо иное, чем 15 дюймов.
Пример: двухвыборочный t-критерий
Определение: Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей или нет.
Пример: Исследователи хотят знать, имеют ли два разных вида растений в данной стране одинаковую среднюю высоту. Они собирают случайную выборку из 20 растений каждого вида и записывают высоту каждого растения в дюймах.
На следующем снимке экрана показано, как выполнить t-тест для двух выборок с использованием функции T.TEST() , чтобы определить, равны ли средние высоты двух популяций:
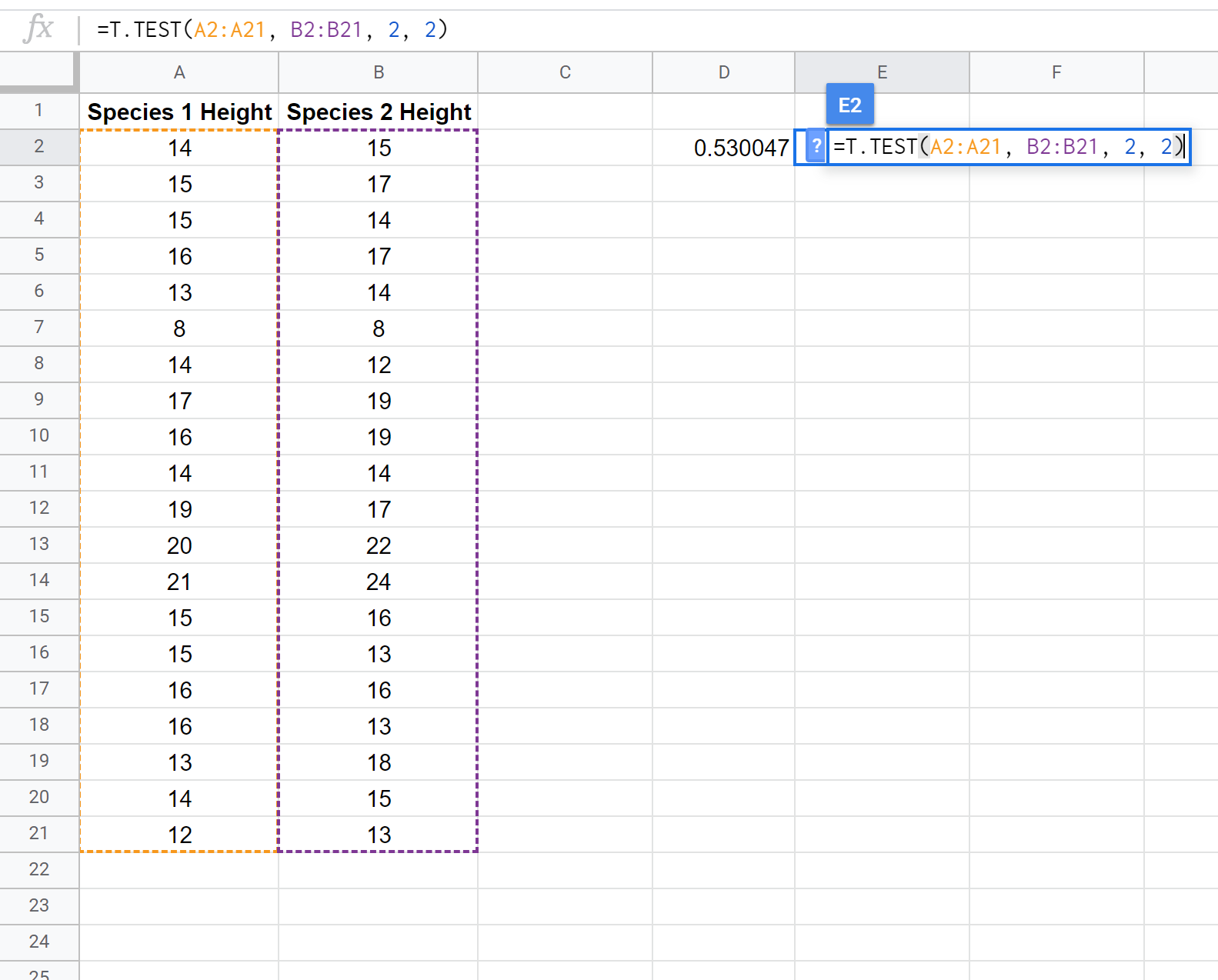
Примечание. Также возможно выполнить односторонний двухвыборочный t-критерий с предположением или без предположения, что две выборки имеют одинаковую дисперсию. Обратитесь к документации T.TEST , чтобы узнать, как скорректировать предположения теста.
Две гипотезы для этого двухвыборочного t-критерия:
H 0 : μ 1 = μ 2 (два средних значения совокупности равны)
H 1 : μ 1 ≠ μ 2 (два средних значения совокупности не равны)
Поскольку значение p нашего теста (0,530047) больше, чем альфа = 0,05, мы не можем отвергнуть нулевую гипотезу теста. У нас нет достаточных доказательств, чтобы сказать, что средняя высота этого конкретного вида растений составляет что-либо иное, чем 15 дюймов.
Пример: t-критерий парных выборок
Определение: t-критерий парных выборок используется для сравнения средних значений двух выборок, когда каждое наблюдение из одной выборки может быть связано с наблюдением из другой выборки.
Пример. Мы хотим знать, оказывает ли курс обучения существенное влияние на успеваемость учащихся на конкретном экзамене. Чтобы проверить это, мы просим 20 учеников в классе пройти предварительный тест. Затем каждый из студентов участвует в учебной программе в течение двух недель. Затем учащиеся повторно сдают тест аналогичной сложности.
На следующем снимке экрана показано, как выполнить парный выборочный t-критерий, чтобы сравнить разницу между средними баллами первого и второго тестов:
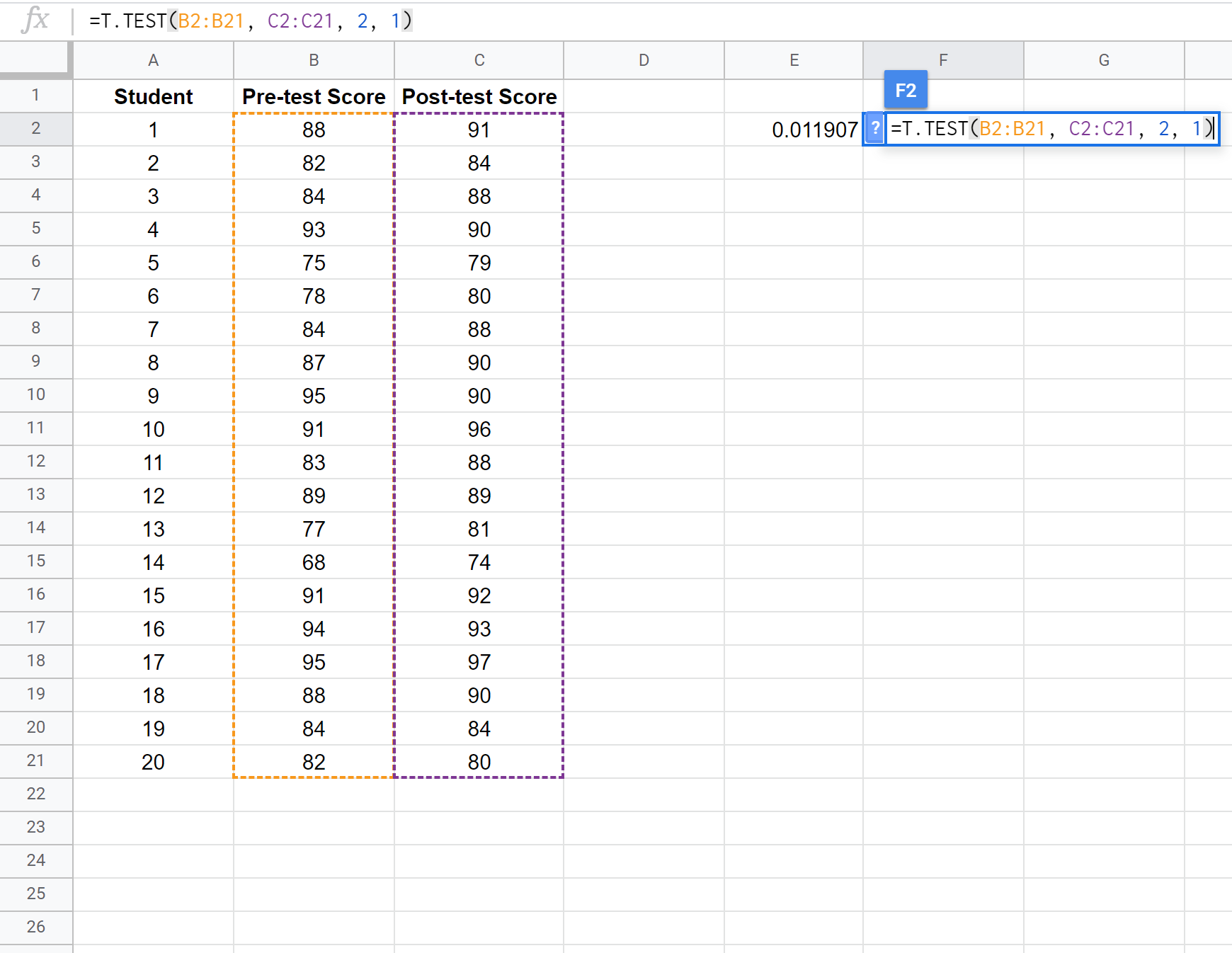
Примечание. Также возможно выполнить односторонний двухвыборочный t-критерий с предположением или без предположения, что две выборки имеют одинаковую дисперсию. Обратитесь к документации T.TEST , чтобы узнать, как скорректировать предположения теста.
Два предположения для этого t-критерия для парных выборок:
H 0 : μ 1 = μ 2 (два средних значения совокупности равны)
H 1 : μ 1 ≠ μ 2 (два средних значения совокупности не равны)
Поскольку значение p нашего теста (0,011907) меньше альфа = 0,05, мы отвергаем нулевую гипотезу теста. У нас есть достаточно доказательств, чтобы сказать, что существует статистически значимая разница между средним баллом до и после теста.